복습
# loss
오차, 손실, error
# loss function
손실함수
# cost function
비용함수
# 목적함수
objective function
- 최소값을 찾는 최적화 문제에서 사용하는 함수. 비용함수 혹은 손실함수로 불리기도 한다
# learning_rate(eta)
훈련 정도, 학습률
# n_estimators
사용할 트리 수
# subsample
전체중에서 overfitting을 방지하기 위해 설정하는 옵션. 1보다 작은 값으로 설정이 가능하다
기본값은1
# early_stopping_rounds =
학습 진행 중 설정한 수 만큼 돌렸음에도 더이상 차도가 없어보이면 멈추겠다는 옵션
# bootsrapping으로 데이터를 나눌 때 한 데이터가 여러번 뽑히거나, 아예 안뽑히는 데이터가 생길 수도 있다.
O
# GBM보다 실행속도가 빠른 알고리즘 두가지
XGBoost, LightGBM
# voting 방식과 Bagging 방식의 차이는?
여러 트리를 돌린다는 점은 같다고 볼 수 있지만
Bagging은'동일한 분류기'로 데이터 샘플링만 서로 다르게 가져가면서 결과를 내는 것이 차이
[출제자 답변]
voting : 모든 데이터에 대하여 서로 다른 알고리즘을 가진 분류기 사용 후 결합한 것이다
Bagging : 1개의 알고리즘과 여러개의 데이터 샘플을 가진다.
# 앙상블 기법의 조건
- 각각의 분류기는 상호 독립적이어야 한다
- 각 분류기의 오분류율은 적어도 50% 보다는 낮아야 한다
# 틀린 것을 고르세요
# 1. 앙상블 학습의 목표는 다양한 의견을 수렴하여 신뢰성 높은 예측값을 얻는 것이다
# 2. 보팅은 서로 다른 알고리즘을 갖는 것이다
# 3. 배깅은 데이터 샘플링은 서로 다르게 하지만 같은 알고리즘을 갖는다
# 4. 보팅 방식의 대표는 랜덤 포레스트이다.
# 5. 배깅 방식은 중첩을 허용한다.
4 - 랜덤 포레스트는 배깅의 대표 방식
# 틀린 것을 고르세요.
# 1. 하드 보팅은 다수결의 원칙과 비슷하고, 소프트 보팅은 각 확률의 평균하여 예측 결정한다.
# 2. 보팅 방식은 여러개의 분류기를 결합한다고 해서 예측 성능이 좋아지지 않는다.
# 3. 랜덤 포레스트는 각자의 데이터 샘플링을 하고 최종적으로 소프트 보팅으로 예측 결정한다.
# 4. 부트스트래핑이란 데이터를 중첩되게 샘플링하는 것이다.
# 5. 랜덤 포레스트의 트리를 분할하는 피처를 참조 시 sqrt(전체)가 아닌 전체이다.
5 - 결정트리에서는 디폴트 값이 전체 피처 이지만, 랜덤포레스트에서는 전체 피처의 sqrt 만큼 참조한다
# 틀린 것을 고르세요.
# 1. 부스팅 방식은 잘못 예측한 데이터에 가중치를 부여해서 오류를 개선해가는 학습 방식이다.
# 2. GBM은 경사하강법을 사용한다.
# 3. GBM은 랜덤포레스트 보다 예측성능이 뛰어나지만 시간이 오래 걸린다는 단점이 있다.
# 4. XGBoost는 랜덤포레스트보다는 속도가 느리지만 GBM에 비해 학습 속도가 빠르다.
# 5. 파이썬 XGBoost와 사이킷런 XGBoost는 early_stopping_rounds를 제공하지 않는다.
1
[출레자 답변]
5...?
# XGBoost 에서 과적합 문제를 해결하기 위해 고려해야 할 사항이 아닌 것은?
# a. max_depth 값을 낮춘다.
# b. min_child_weight 값을 낮춘다.
# c. gamma 값을 높인다.
# d. eta 값을 낮춘다.
b - 클수록 분할을 자제한다. 과적합 조절용
# 앙상블 학습 방식 중 맞추기 어려운 문제를 맞추는 것을 목적으로 하는. 에러에 가중치를 주는 방식은?
GBM
[출제자 답변]
Boosting
# 분류기들의 레이블 값 결정 확률을 모두 더하고, 이를 평균하여
# 확률이 가장 높은 레이블 값을 최종 보팅 결과값으로 선정하는 보팅 방식은
소프트 보팅
# 머신러닝에서 여러개의 분류기로 데이터를 학습하고 각각 학습된 알고리즘으로 결과를 예측,
# 그 결과들을 결합해 최종으로 더 나은 결과를 도출해내는 방식을 무엇이라고 하나요?
앙상블 학습
# 머신러닝에서 앙상블의 대표적인 유형 3가지
voting, Bagging, Bossting
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
from sklearn.ensemble import VotingClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
iris = load_iris()
lr_clf = LogisticRegression(solver='liblinear')
knn_clf = KNeighborsClassifier(n_neighbors=8)
gnb_clf = GaussianNB()
vo_clf =
# vo_clf 에 알맞은 내용을 넣어주세요
vo_clf = VotingClassifier(estimators=[('LR', lr_clf), ('KNN', knn_clf)], voting='soft')LightGBM
XGBoost와 동일하게 조기 중단(early stopping)이 가능하다. XGBClassifier와 동일하게 LGBMClassifier의 fit()에 조기 중단 관련 파라미터를 설정해주면 된다.
[장단점]
- XGB보다 학습에 걸리는 시간이 훨씬 적으며 메모리 사용량도 상대적으로 적다
- 카테고리형 피처를 자동 변환하고, 예측 성능에서 큰 차이를 보이지 않는다
- 적은 데이터 셋에 적용할 경우 과적합이 발생하기 쉽다는 것은 아쉬운점(적은 데이터 셋의 기준은 애매하지만 LightGBM의 공식 문서에서는 일반적으로 10,000건 이하의 데이터 셋 정도라고 기술하고 있다.)
[트리기반 알고리즘의 특징]
- 트리의 깊이를 효과적으로 줄이기 위한 균형 트리 분할(Level Wise) 방식을 사용한다. 최대한 균형 잡힌 트리를 유지하면서 분할하기 때문에 깊이가 최소화되며 오버피팅에 보다 강한 구조를 가진다
- 하지만 균형을 맞추기 위한 시간이 꽤 걸린다는 단점
[LightGBM의 특징]
- 일반 GBM 계열의 트리 분할 방식과는 다르게 리프 중심 트리 분할(Leaf Wise) 방식을 사용
- 트리의 균형을 맞추지 않기 때문에 비태징적인 규칙 트리가 생성, 최대 손실 값을 가지는 리프 노드를 지속적으로 분할하여 깊이가 증가하게 된다.
- 이렇게 생성된 규칙트리는 학습을 반복할 수록 결국은 균형 트리 분할 방식보다 예측 오류 손실을 최소화할 수 있다는 것이 구현 사상이다.
주요 파라미터(사이킷런 기준)
n_estimators[default:100]: GBM과 XGB의 n_estimators와 같은 파라미터learning_rate [defalut: 0.1]: GBM과 XGB의 학습률(learning_rate)과 같은 파라미터, 일반적으로 n_estimators를 높이고 learning_rate를 낮추면 예측 성능이 향상하지만 마찬가지로 과적합 이슈 및 소요 시간 증가의 문제가 있다.max_depth [default: 1]: 트리 기반 알고리즘의 max_depth와 같다. 0보다 작은 값을 지정하면 깊이 제한이 없다. LightGBM은 Leaf Wise 방식이므로 깊이가 상대적으로 더 깊어질 수 있다.min_child_samples [default: 20]: 결정 트리의 min_samples_leaf와 같은 파라미터로 리프 노드가 되기 위해 최소한으로 필요한 샘플 수num_leaves [default: 31]: 하나의 트리가 가질 수 있는 최대 리프 개수boosting [default: gbdt]: 부스팅의 트리를 생성하는 알고리즘을 지정하며 'gbdt'는 일반적인 그래디언트 부스팅 결정 트리이며 'rf'는 랜덤 포레스트subsample [default: 1]: GBM과 XGB의 subsample과 같은 파라미터colsample_bytree [default: 1]: XGB의 colsample_bytree와 같은 파라미터로 개별 트리를 학습할 때마다 무작위로 선택하는 피처의 비율reg_lambda [default: 0]: XGB의 reg_lambda와 같은 파라미터로 L2 regulation 제어를 위한 값이다. 피처 개수가 많을 경우 적용을 검토하며 값이 클수록 과적합 감소 효과가 있다.reg_alpha [default: 0]: XGB의 reg_alpha와 같은 파라미터로 L1 regulation 제어를 위한 값이다. 피처 개수가 많을 경우 적용을 검토하며 값이 클수록 과적합 감소 효과가 있다.- 학습 태스크 파라미터
objective: 최소값을 가져야할 손실함수를 정의한다. XGB의 objective 파라미터와 동일
하이퍼 파라미터 튜닝 방안
num_leaves의 개수를 중심으로 min_child_samples(min_data_in_leaf, max_depth를 함께 조정하면서 모델의 복잡도를 줄이는 것이 기본 튜닝 방안이다.
learning_rate 를 작게 하면서 n_estimators를 크게 하는 것은 부스팅 계열 튜닝에서 가장 기본적인 튜닝 방안이므로 이를 적용하는 것도 좋다. 물론 n_estimators를 너무 크게 하는 것은 과적합으로 오히려 성능이 저하될 수도 있다는 것은 유념해야할 것
적용 - 위스콘신 유방암 예측
LightGBM 설치
!pip install lightgbm
# 버젼확인
lightgbm.__version__
# '3.3.3'데이터 가져오기
# LightGBM에 파이썬 패키지인 lightgbm 에서 LGBMClassifier import
from lightgbm import LGBMClassifier
import pandas as pd
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
dataset = load_breast_cancer()
dataset데이터 변수에 할당 및 나누기
cancer_df = pd.DataFrame(data=dataset.data, columns=dataset.feature_names)
cancer_df['target']=dataset.target
X_features = dataset.data
y_label = dataset.target
# 전체 데이터 중 80을 학습용으로 20을 데이터 용으로 추출
X_train, X_test, y_train, y_test = train_test_split(X_features, y_label, test_size=0.2, random_state=11)
# 위에서 만든 X_train, y_train을 다시 쪼개서 90은 학습, 10은 검증용으로 분리
X_tr, X_val, y_tr, y_val = train_test_split(X_train, y_train, test_size=0.1, random_state=11)학습
# 앞서 XGBoost와 동일하게 n_estimators는 400
lgbm_wrapper = LGBMClassifier(n_estimators=400, learning_rate=0.05)
# Liglightgbm도 XBoost와 동일하게 조기 중단(early_stopping_rounds) 수행 가능
evals = [(X_tr, y_tr), (X_val, y_val)]
lgbm_wrapper.fit(X_tr, y_tr, early_stopping_rounds=50, eval_metric="logloss", eval_set=evals, verbose=True)
출력을 보면 조기중단 설정으로 인해 150까지만 반복하고 학습을 종료하였다.
LightGBM 예측/평가
# 사용할 사용자 정의 함수
from sklearn.metrics import accuracy_score, precision_score , recall_score , confusion_matrix, f1_score, roc_auc_score
def get_clf_eval(y_test, pred = None, pred_proba = None) :
confusion = confusion_matrix(y_test, pred) # 오차행렬
accuracy = accuracy_score(y_test, pred) # 정확도
precision = precision_score(y_test, pred) # 정밀도
recall = recall_score(y_test, pred) # 재현율
f1 = f1_score(y_test, pred) # F1 스코어
# ROC-AUC
roc_auc = roc_auc_score(y_test, pred_proba)
print('오차행렬')
print(confusion)
print()
# ROC-AUC 추가
print(f'정확도:{accuracy:.4f}, 정밀도:{precision:.4f}, 재현율:{recall:.4f}, f1_score:{f1:.4f}, AUC:{roc_auc:.4f}')
# 예측
preds = lgbm_wrapper.predict(X_test)
pred_proba = lgbm_wrapper.predict_proba(X_test)[:,1]
# 평가
get_clf_eval(y_test, preds, pred_proba)오차행렬
[[36 2]
[ 0 76]]
정확도:0.9825, 정밀도:0.9744, 재현율:1.0000, f1_score:0.9870, AUC:1.0000피처별 중요도 시각화하여 보기
# plot_imporance()를 이용하여 feature중요도 시각화
from lightgbm import plot_importance
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10, 12))
plot_importance(lgbm_wrapper, ax=ax)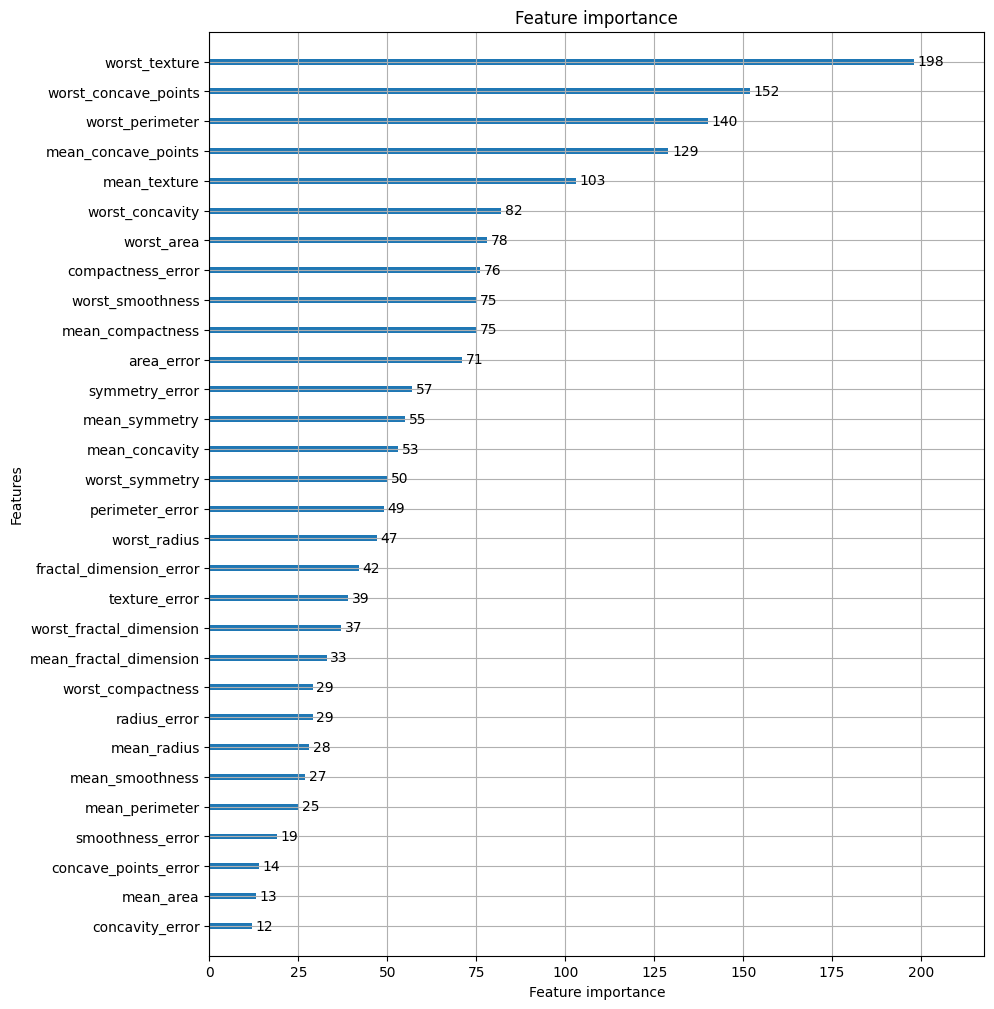
베이지안 최적화 기반의 하이퍼 파라미터 튜닝
지금까지는 튜닝을 위해 사이킷런에서 제공하는 Grid Search 방식을 적용했다. 이 방식의 주요한 단점 한가지는, 튜닝해야할 파라미터 개수가 많을 경우 최적화 수행시간이 오랜 걸린다는 것이다. 개별 하이퍼 파라미터 값의 범위가 넓거나 학습 데이터가 대용량일 경우에는 더욱 늘어나게 된다.
베이지안 최적화는 베이지안 확률에 기반을 두고 있는 최적화 기법이다. 구성하는 두가지 중요 요소는 대체모델(Surrogate Model)과 획득 함수(Acquisition function)이다.
- 대체모델 : 획득 함수로부터 최적 함수를 예측할 수 있는 입력값을 추천 받은 뒤 이를 기반으로 최적 함수 모델을 개선
- 획득함수 : 개선된 대체 모델을 기반으로 최적 입력값을 계산
대체 모델은 획득 함수가 계산한 하이퍼 파라미터를 입력받으면서 점차적으로 개선되며, 개선된 대체 모델을 기반으로 획득 함수는 더 정확한 하이퍼 파라미터를 계산 할 수 있게 된다.
HyperOpt 사용해보기
베이지안 최적화를 머신러닝 모델의 하이퍼 파라미터 튜닝에 적용할 수 있게 제공되는 패키지 중 하나이다. pip install을 통해 설치할 수 있으며 HyperOpt의 주요 로직은 아래와 같다.
첫번째는 입력변수명과 입력값의 공간설정
둘째는 목적함수의 설정
마지막으로 목적함수의 반환최솟값을 가지는 최적 입력값 유추입력 변수명과 입력값 검색 공간은 딕셔너리 형태로 설정한다. key값으로 입력 변수명, value값으로 해당 입력 견수의 검색공간이 주어짐
!pip install hyperopt
from hyperopt import hp
# 2개의 입력변수 x,y에 대해서 입력값 검색 공간을 지정한다.+
# -10 ~ 10까지의 1 간격 설정
# 입력변수 x와 -15 ~ 15까지 1 간격으로 입력 변수 y 설정
search_space = {'x' : hp.quniform('x', -10, 10, 1), 'y' : hp.quniform('y', -15, 15, 1)}입력값의 검색 공간을 제공하는 대표적 함수들은 아래와 같다. 함수인자로 들어가는 label은 입력 변수명을 다시 적어주어야 하며 (low : 최소값 / high : 최댓값 / q : 간격)이다.
hp.quniform(label, low, hight, q) : label로 지정된 입력값 변수 검색 공간을 최솟값 low에서 최대값 high까지의 q 간격을 가지고 설정
hp.uniform(label, low, high) : 최소값 low에서 최대값 high까지 정규 분포 형태의 검색 공간 설정
hp.randint(label, upper) : 0부터 최대값 upper까지 random한 정수값으로 검색 공간 설정
hp.loguniform(label, low, hight) : exp(uniform(low, high) 값을 반환하며, 반환 값의 log 변환 된 값은 정규 분포 형태를 가지는 검색 공간 설정
hp.choice(label, options) : 검색 값이 문자열 또는 문자열과 숫자값이 섞여있을 경우 설정, options는 리스트나 튜플형태로 제공되며
hp.choice('tree_criterion', ['gini', 'entropy'])와 같이 설정하면 입력변수 tree_criterion의 값을 gini와 entropy로 설정하여 입력한다.목적함수는 반드시 변수값과 검색 공간을 가지는 딕셔너리를 인자로 받고, 특정 값을 반환하는 구조로 만들어져야한다.
from hyperopt import STATUS_OK
# 목적 함수를 생성, 변수값과 변수 검색 공간을 가지는 딕셔너리를 인자로 받고, 특정 값을 반환
def objective_func(search_space) :
x = search_space['x']
y = search_space['y']
retval = x**2 - 20*y
return retval목적 함수의 반환값이 최소가 될 수 있는 최적의 입력값을 베이지안 최적화 기법에 기반하여 찾아줘야한다. HyperOpt는 이런 기능을 수행할 수 있는 함수가 있다.
fmin(objective, space, algo, max_evals, trials
fn : 위에서 생성한 objective_func와 같은 목적 함수
space : 위에서 생성한 search_space와 같은 검색공간 딕셔너리
algo : 베이지안 최적화 적용 알고리즘. 기본적으로 tpe.suggest이며 이는 HyperOpt의 기본 최적화 알고리즘인 TPE(Tree of Parzen Estimator)을 의미한다
max_evals : 최적 입력값을 찾기 위한 입력값 시도 횟수
trials : 최적 입력값을 찾기 위해 시도한 입력값 및 해당 입력값의 목적함수 반환값 결과를 저장하는데 사용된다. Trials클래스를 객체로 생성한 변수명을 입력
rstate : fmin()을 수행할 때마다 동일한 결과값을 가질 수 있도록 설정하는 랜덤 시드(seed)값from hyperopt import fmin, tpe, Trials
# 입력 결과값을 저장한 Trials 객체값 생성
trial_val = Trials()
# 목적 함수의 최소값을 반환하는 최적 입력 변수값을 5번 입력값 시도(max_evals = 5)로 찾아내보자
best_01 = fmin(fn=objective_func, space=search_space, algo=tpe.suggest, max_evals=5, trials=trial_val
# rstate는 결과값이 책과 동일하게 만들기 위해 적용한것으로 일반적으로는 잘 이용안함
, rstate=np.random.default_rng(seed=0))
print('best : ', best_01)100%|█████████████████████████████████████████████████████████████| 5/5 [00:00<00:00, 835.55trial/s, best loss: -224.0]
best : {'x': -4.0, 'y': 12.0}# max_evals값을 20으로 수행하도록 하면 어떤 최적값을 반환하는지 살펴보기
best_02 = fmin(fn=objective_func, space=search_space, algo=tpe.suggest, max_evals=20, trials=trial_val
# rstate는 결과값이 책과 동일하게 만들기 위해 적용한것으로 일반적으로는 잘 이용안함
, rstate=np.random.default_rng(seed=0))
print('best : ', best_02)100%|███████████████████████████████████████████████████████████| 20/20 [00:00<00:00, 578.48trial/s, best loss: -296.0]
best : {'x': 2.0, 'y': 15.0}목적함수의 반환값을 x**2 - 20*y로 설정했으므로 x는 0에 가까울수록 y는 15에 가까울수록 반환값이 최소로 근사될 수 있다. 20번으로 설정한 후 결과값이 x는 2 y는 15의 결과가 나왔으므로 꽤 주시할만 한 결과이다.
HyperOpt를 이용한 XGB 하이퍼 파라미터 최적화
# 아까 불러와줬던 위스콘신 유방암 데이터 셋 사용
dataset
X_train, X_test, y_train, y_test=train_test_split(X_features, y_label, test_size=0.2, random_state=150)
# 위에서 만든 X_train, y_train을 다시 쪼개서 90은 학습, 10은 검증용으로 분리
X_tr, X_val, y_tr, y_val = train_test_split(X_train, y_train, test_size=0.1, random_state=11)max_dept는 5에서 20까지 1 간격으로, min_child_weight는 1에서 2까지 1간격으로 설정하기 위해 hp.quniform()을 사용하고, colsample_bytree는 0.5에서 1사이, learning_rate는 0.01에서 0.2 사이 정규 분포된 값으로 검색하기 위해 hp.uniform()을 사용하겠다.
from hyperopt import hp
# max_dept는 5에서 20까지 1 간격으로, min_child_weight는 1에서 2까지 1간격으로
# colsample_bytree는 0.5에서 1사이, learning_rate는 0.01에서 0.2 사이 정규 분포된 값으로 검색.
xgb_search_space = {'max_depth': hp.quniform('max_depth', 5, 20, 1),
'min_child_weight': hp.quniform('min_child_weight', 1, 2, 1),
'learning_rate': hp.uniform('learning_rate', 0.01, 0.2),
'colsample_bytree': hp.uniform('colsample_bytree', 0.5, 1),
} 이제 목적함수를 설정한다. 유의할 사항은 두가지인데
- 첫째, 검색 공간에서 목적 함수로 입력되는 모든 인자들은 실수형 값이므로 이들을 XGBoostClassifier의 정수형 하이퍼 파라미터 값으로 설정 할 때는 정수형으로 형변환을 해야한다.
- 두번째, HyperOpt의 목적 함수는 최소값을 반환할 수 있도록 최적화해야하기 때문에 정확도와 같이 값이 클수록 좋은 성능지표를 뽑아낼 경우, -1을 곱한뒤 반환해야 한다.
이를 유의하면서 목적함수를 작성해보도록 하자. 반환값은 교차 검증 기반인 평균 정확도(accuracy)를 사용하겠다. 아쉬운 것은 cross_val_score()를 XGBoost나 LightGBM에 적용할 경우 조기 중단(early stopping)이 지원되지 않는다는 점이다. 조기 중단을 위해서는 KFold로 학습과 검증용 데이터 셋을 만들어 직접 교차 검증을 수행해야 함
from sklearn.model_selection import cross_val_score
from xgboost import XGBClassifier
from hyperopt import STATUS_OK
# fmin()에서 입력된 search_space 값으로 입력된 모든 값은 실수형임.
# XGBClassifier의 정수형 하이퍼 파라미터는 정수형 변환을 해줘야 함.
# 정확도는 높을수록 더 좋은 수치임. -1 * 정확도를 곱해서 큰 정확도 값일수록 최소가 되도록 변환
def objective_func(search_space):
# 수행 시간 절약을 위해 nestimators는 100으로 축소
xgb_clf = XGBClassifier(n_estimators=100, max_depth=int(search_space['max_depth']),
min_child_weight=int(search_space['min_child_weight']),
learning_rate=search_space['learning_rate'],
colsample_bytree=search_space['colsample_bytree'],
eval_metric='logloss')
accuracy = cross_val_score(xgb_clf, X_train, y_train, scoring='accuracy', cv=3)
# accuracy는 cv=3 개수만큼 roc-auc 결과를 리스트로 가짐. 이를 평균해서 반환하되 -1을 곱함.
return {'loss':-1 * np.mean(accuracy), 'status': STATUS_OK} fmin()을 이용해 최적 하이퍼 파라미터를 도출해보자
from hyperopt import fmin, tpe, Trials
trial_val = Trials()
best = fmin(fn=objective_func,
space=xgb_search_space,
algo=tpe.suggest,
max_evals=50, # 최대 반복 횟수 지정
trials=trial_val, rstate=np.random.default_rng(seed=9))
print('best : ', best)100%|███████████████████████████████████████████████| 50/50 [00:11<00:00, 4.46trial/s, best loss: -0.9517398629022887]
best : {'colsample_bytree': 0.5036717216371022, 'learning_rate': 0.19808959234346474, 'max_depth': 12.0, 'min_child_weight': 1.0}위 출력결과에서 보이듯 max_depth, min_child_weight가 실수형 값으로 도출되었음을 유의해야한다.
도출된 최적 하이퍼 파라미터를 이용해 XGBClassifier를 재학습한 후 성능평가를 해보자
xgb_wrapper = XGBClassifier(n_estimators=400,
learning_rate=round(best['learning_rate'], 5),
max_depth=int(best['max_depth']),
min_child_weight=int(best['min_child_weight']),
colsample_bytree=round(best['colsample_bytree'], 5)
)
evals = [(X_tr, y_tr), (X_val, y_val)]
# 재학습
# verbose=False = 진행되는거 안봐도 괜찮다
xgb_wrapper.fit(X_tr, y_tr, early_stopping_rounds=50, eval_metric='logloss', eval_set=evals, verbose=False)
# 예측
preds = xgb_wrapper.predict(X_test)
pred_proba = xgb_wrapper.predict_proba(X_test)[:,1]
get_clf_eval(y_test, preds, pred_proba)[[40 2]
[ 0 72]]
정확도:0.9825, 정밀도:0.9730, 재현율:1.0000, f1_score:0.9863, AUC:0.9937분류 실습 - 캐글 산탄데르 고객 만족 예측
370개의 피처로 주어진 데이터 세트에 기반하여 고객 만족 여부를 예측한다. 피처 이름은 모두 익명처리 되어 이름만 가지고는 어떤 속성인지 추정할 수 없으며, 클래스 레이블 명은 Target. 이 값이 1이면 불만을 가진 고객 0이면 만족한 고객이다.
데이터 불러오기+전처리
kaggle에서 받아온 데이터를 사용중인 폴더(Working directory)에 넣어준 후 불러왔다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
cust_df = pd.read_csv("./santander_customer/train.csv")
print('dataset shape : ', cust_df.shape)
cust_df[:3]
label로 사용할 TARGET 컬럼의 비율이 궁금하니 검색해보기로 한다
cust_df.TARGET.value_counts()/len(cust_df)
>
0 0.960431
1 0.039569
Name: TARGET, dtype: float64오홍... 굉장히 불균형하다. 대부분이 만족(0)이므로 정확도 보다는 ROC-AUC로 성능을 평가하기로 하고, describe()메서드를 이용해 각 피처의 값 분포를 확인해보면
cust_df.describe()
이와 같은데, var3을보면 min(최소값)에 갑자기 -999999 값이 튀어나온 모습을 확인할 수 있다. 이는 NaN이나 특정 예외 값을 이와 같이 변환했다고 생각해 볼 수 있으나, 다른 값에 비해 너무 편차가 크므로 해당 수를 replace하여 값이 가장 많은 2로 변환하기로 한다.
cust_df['var3'] = cust_df['var3'].replace(-999999, 2)
# 변환 후 값 확인
cust_df['var3'].value_counts()
# 2 74281
# 8 138
# 9 110
# 3 108
# 1 105
# ...
# 231 1
# 188 1
# 168 1
# 135 1
# 87 1
# Name: var3, Length: 207, dtype: int64
cust_df['var3'].min()
# 0ID는 지우고, Target은 label로 분리
cust_df.drop(['ID'], axis=1, inplace = True)
X_features = cust_df.iloc[:,:-1]
y_label = cust_df.iloc[:, -1]
X_features.shape
# (76020, 369)학습과 성능 평가를 위해 원본 데이터 set에서 train data set과 test data set를 분리한다. XGB의 조기 중단(early stopping)의 검증 데이터 셋으로 사용하기 위해 X_train, y_train을 쪼개서 학습과 검증 데이터 셋트로 한번 더 나눠준다.
# train과 test 셋 나눠주기
X_train, X_test, y_train, y_test = train_test_split(X_features, y_label, test_size=0.2, random_state=11)
# 나눠준 train 데이터를 다시 학습과 검증 데이터로 분리
# 조기중단(early stopping)을 위하여
X_tr, X_val, y_tr, y_val = train_test_split(X_train, y_train, test_size=0.3, random_state=11)XGB 모델 학습과 하이퍼 파라미터 튜닝
학습 모델을 생성하고 예측 결과를 ROC-AUC로 평가해보기로 한다. 따라서 XGBClassifier의 eval_metric는 'auc'로 설정(하지만 logloss로 해도 큰 차이는 없다고 한다.). 앞에서 분리한 학습과 검증 데이터 셋을 이용하여 조기 중단은 100회로 설정한다.
from xgboost import XGBClassifier
from sklearn.metrics import roc_auc_score
# n_estimators는 500으로, random state는 예제 수행 시마다 동일 예측 결과를 위해 설정
xgb_clf = XGBClassifier(n_estimators=500, learning_rate=0.05, random_state=156)
# 성능 평가 지표를 aux로, 조기 중단 파라미터는 100으로 설정하고 학습 수행
xgb_clf.fit(X_tr, y_tr, early_stopping_rounds=100, eval_metric='auc', eval_set=[(X_tr, y_tr), (X_val, y_val)])

쭉 뽑혀나온다. 500번 학습을 설정하였으나 조기 중단으로 269까지만 한 모습을 확인할 수 있었다.
# 테스트 데이터 셋으로 ROC-AUC 값 확인하기
xgb_roc_score = roc_auc_score(y_test, xgb_clf.predict_proba(X_test)[:,1])
print(f'ROC AUC : {xgb_roc_score}')ROC AUC : 0.8326294708915177예측
preds = xgb_clf.predict(X_test)
accuracy_score(y_test, preds)0.9606682451986319예상 정확도가 약 96.0% 로 뽑혔다. 와우. HyperOpt를 이용하여 베이지안 최적화 기반으로 XGB의 하이퍼 파라미터 튜닝을 수행해보자.
검색 공간 설정
# 하이퍼 파라미터 검색 공간 설정
# max_depth는 5에서 15까지 간격 1로
xgb_search_space = {'max_depth': hp.quniform('max_depth', 5, 15, 1),
# min_child_weight는 1에서 6까지 간격 1로
'min_child_weight': hp.quniform('min_child_weight', 1, 6, 1),
# colsample_bytree는 0.5에서 0.95사이
'colsample_bytree': hp.uniform('colsample_bytree', 0.5, 0.95),
# learning_rate는 0.01에서 0.2사이 정규 분포된 값
'learning_rate': hp.uniform('learning_rate', 0.01, 0.2)
}목적함수 만들기
3 Fold 교차검능을 이용해 평균 ROC-AUC값을 반환하되 -1을 곱해주어 최대 ROC-AUC값이 최소 반환값이 되도록 한다.
from sklearn.model_selection import KFold
from sklearn.metrics import roc_auc_score
# 목적 함수 설정.
# 추후 fmin()에서 입력된 search_space값으로 XGBClassifier 교차 검증 학습 후 -1* roc_auc 평균 값을 반환.
def objective_func(search_space):
# 하이퍼 파라미터 검색 공간
xgb_clf = XGBClassifier(n_estimators=100, max_depth=int(search_space['max_depth'])
, min_child_weight=int(search_space['min_child_weight'])
, colsample_bytree=search_space['colsample_bytree']
, learning_rate=search_space['learning_rate']
)
# 3개 k-fold 방식으로 평가된 roc_auc 지표를 담는 list
roc_auc_list= []
# 3개 k-fold방식 적용
kf = KFold(n_splits=3)
# X_train을 다시 학습과 검증용 데이터로 분리
for tr_index, val_index in kf.split(X_train):
# kf.split(X_train)으로 추출된 학습과 검증 index값으로 학습과 검증 데이터 세트 분리
X_tr, y_tr = X_train.iloc[tr_index], y_train.iloc[tr_index]
X_val, y_val = X_train.iloc[val_index], y_train.iloc[val_index]
# early stopping은 30회로 설정하고 추출된 학습과 검증 데이터로 XGBClassifier 학습 수행.
xgb_clf.fit(X_tr, y_tr, early_stopping_rounds=30, eval_metric='auc'
, eval_set=[(X_tr, y_tr), (X_val, y_val)])
# 1로 예측한 확률값 추출후 roc auc 계산하고 평균 roc auc 계산을 위해 list에 결과값 담음.
score = roc_auc_score(y_val, xgb_clf.predict_proba(X_val)[:, 1])
roc_auc_list.append(score)
# 3개 k-fold로 계산된 roc_auc값의 평균값을 반환하되,
# HyperOpt는 목적함수의 최소값을 위한 입력값을 찾으므로 -1을 곱한 뒤 반환.
return -1 * np.mean(roc_auc_list) fmin()
fmin() 함수를 호출해 max_eval=50회 반복하며 최적의 하이퍼 파라미터를 도출하자. 50회만큼의 교차 검증이 반복되며 학습/평가를 하기 때문에 꽤 시간이 걸린다.
from hyperopt import fmin, tpe, Trials
trials = Trials()
# fmin()함수를 호출, 목적함수의 최소값을 가지는 최적 입력값을 추출하자
best = fmin(fn=objective_func,
space=xgb_search_space,
algo=tpe.suggest,
# 지정된 횟수만큼 반복
max_evals=50,
trials=trials, rstate=np.random.default_rng(seed=30)
)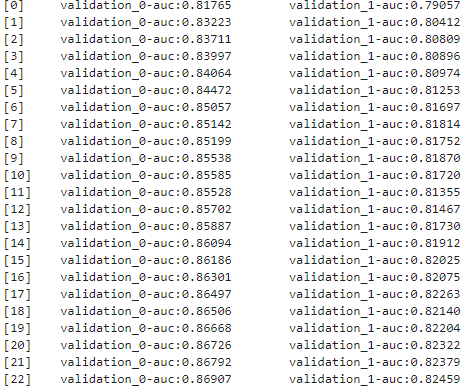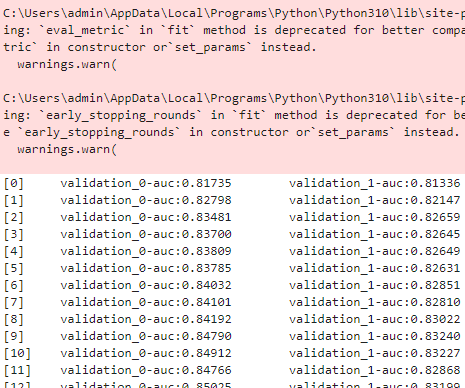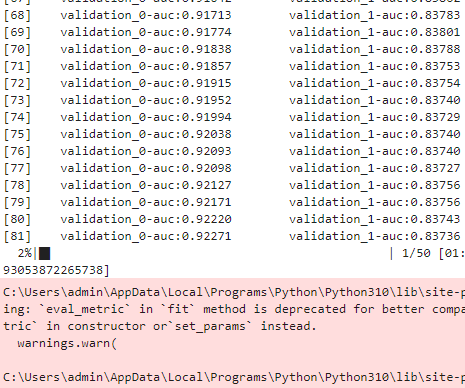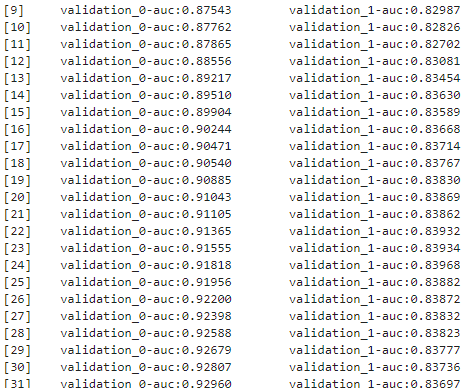
정말 오래 걸린다. 한 30-40분 걸린듯
print('best : ', best)
>
.
.
.
.
best : {'colsample_bytree': 0.5659263778337817, 'learning_rate': 0.09882594691417974, 'max_depth': 5.0, 'min_child_weight': 6.0}도출된 최적 하이퍼 파라미터를 기반으로 XGBClassifier를 재학습시키고 데스트 데이터 셋에서 ROC-AUC를 측정해 보자.
# n_estimators를 500으로 증가 후
# 찾아낸 최적 하이퍼 파라미터를 기반으로 학습/예측 수행
xgb_clf = XGBClassifier(n_estimators=500,
learning_rate=int(best['learning_rate']),
max_depth=int(best['max_depth']),
min_child_weight=int(best('min_child_weight')),
colsample_bytree=found(best['colsample_bytree'])
)
# evaluation metric을 하나의 auc로 하고
# 조기중단은 100으로 설정후 학습 수행
xgb_clf.fit(X_tr, y_tr, early_stopping_rounds=100, eval_metric='auc', eval_set=[(X_tr, y_tr), (X_val, y_val)])
xgb_roc_score=roc_auc_score(y_test, xgb_clf.predict_proba(X_test)[:,1])
print(xgb_roc_score)[0] validation_0-auc:0.50000 validation_1-auc:0.50000
[1] validation_0-auc:0.50000 validation_1-auc:0.50000
[2] validation_0-auc:0.50000 validation_1-auc:0.50000
[3] validation_0-auc:0.50000 validation_1-auc:0.50000
[4] validation_0-auc:0.50000 validation_1-auc:0.50000
[5] validation_0-auc:0.50000 validation_1-auc:0.50000
[6] validation_0-auc:0.50000 validation_1-auc:0.50000
[7] validation_0-auc:0.50000 validation_1-auc:0.50000
[8] validation_0-auc:0.50000 validation_1-auc:0.50000
[9] validation_0-auc:0.50000 validation_1-auc:0.50000
[10] validation_0-auc:0.50000 validation_1-auc:0.50000
[11] validation_0-auc:0.50000 validation_1-auc:0.50000
[12] validation_0-auc:0.50000 validation_1-auc:0.50000
[13] validation_0-auc:0.50000 validation_1-auc:0.50000
[14] validation_0-auc:0.50000 validation_1-auc:0.50000
[15] validation_0-auc:0.50000 validation_1-auc:0.50000
[16] validation_0-auc:0.50000 validation_1-auc:0.50000
[17] validation_0-auc:0.50000 validation_1-auc:0.50000
[18] validation_0-auc:0.50000 validation_1-auc:0.50000
[19] validation_0-auc:0.50000 validation_1-auc:0.50000
[20] validation_0-auc:0.50000 validation_1-auc:0.50000
[21] validation_0-auc:0.50000 validation_1-auc:0.50000
[22] validation_0-auc:0.50000 validation_1-auc:0.50000
[23] validation_0-auc:0.50000 validation_1-auc:0.50000
[24] validation_0-auc:0.50000 validation_1-auc:0.50000
[25] validation_0-auc:0.50000 validation_1-auc:0.50000
[26] validation_0-auc:0.50000 validation_1-auc:0.50000
[27] validation_0-auc:0.50000 validation_1-auc:0.50000
[28] validation_0-auc:0.50000 validation_1-auc:0.50000
[29] validation_0-auc:0.50000 validation_1-auc:0.50000
[30] validation_0-auc:0.50000 validation_1-auc:0.50000
[31] validation_0-auc:0.50000 validation_1-auc:0.50000
[32] validation_0-auc:0.50000 validation_1-auc:0.50000
[33] validation_0-auc:0.50000 validation_1-auc:0.50000
[34] validation_0-auc:0.50000 validation_1-auc:0.50000
[35] validation_0-auc:0.50000 validation_1-auc:0.50000
[36] validation_0-auc:0.50000 validation_1-auc:0.50000
[37] validation_0-auc:0.50000 validation_1-auc:0.50000
[38] validation_0-auc:0.50000 validation_1-auc:0.50000
[39] validation_0-auc:0.50000 validation_1-auc:0.50000
[40] validation_0-auc:0.50000 validation_1-auc:0.50000
[41] validation_0-auc:0.50000 validation_1-auc:0.50000
..
이하생략# 피처의 중요도를 시각화하여 보기
from xgboost import plot_importance
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1, figsize=(10, 8))
plot_importance(xgb_clf, ax=ax, max_num_features=20, height=0.4)
LightGBM을 직접 수행해보면서 XGB보다는 학습에 걸리는 시간이 좀 더 단축되었음을 느낄 수 있었다.
# LightGBM 모델 학습과 하이퍼 파라미터 튜닝
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=500)
eval_set=[(X_tr, y_tr), (X_val, y_val)]
lgbm_clf.fit(X_tr, y_tr, early_stopping_rounds=100, eval_metric='auc', eval_set=eval_set)
lgbm_roc_score = roc_auc_score(y_test, lgbm_clf.predict_proba(X_test)[:,1])
print(f'ROC-AUC : {lgbm_roc_score}')[1] training's auc: 0.830333 training's binary_logloss: 0.158262 valid_1's auc: 0.800033 valid_1's binary_logloss: 0.156656
[2] training's auc: 0.835095 training's binary_logloss: 0.152432 valid_1's auc: 0.806471 valid_1's binary_logloss: 0.15186
[3] training's auc: 0.84184 training's binary_logloss: 0.1482 valid_1's auc: 0.808535 valid_1's binary_logloss: 0.148619
[4] training's auc: 0.847707 training's binary_logloss: 0.144867 valid_1's auc: 0.812339 valid_1's binary_logloss: 0.146112
[5] training's auc: 0.852553 training's binary_logloss: 0.141937 valid_1's auc: 0.816928 valid_1's binary_logloss: 0.14387
[6] training's auc: 0.854143 training's binary_logloss: 0.139571 valid_1's auc: 0.817505 valid_1's binary_logloss: 0.142262
[7] training's auc: 0.857426 training's binary_logloss: 0.137489 valid_1's auc: 0.820769 valid_1's binary_logloss: 0.14087
[8] training's auc: 0.862499 training's binary_logloss: 0.135785 valid_1's auc: 0.824541 valid_1's binary_logloss: 0.139729
[9] training's auc: 0.864169 training's binary_logloss: 0.134334 valid_1's auc: 0.82638 valid_1's binary_logloss: 0.138841
..
이하 생략목적함수 생성. 앞서 XGB와 목적함수가 크게 다르지는 않지만, LGBMClassifer 객체를 생성하는 부분이 다를 뿐이다.
def objective_func(search_space):
# 하이퍼 파라미터 검색 공간
lgbm_clf = LGBMClassifier(n_estimators=100,
num_leaves=int(search_space['num_leaves']),
max_depth=int(search_space['max_depth']),
min_child_samples=int(search_space['min_child_samples']),
subsample=search_space['subsample']
, learning_rate=search_space['learning_rate']
)
# 3개 k-fold 방식으로 평가된 roc_auc 지표를 담는 list
roc_auc_list= []
# 3개 k-fold방식 적용
kf = KFold(n_splits=3)
# X_train을 다시 학습과 검증용 데이터로 분리
for tr_index, val_index in kf.split(X_train):
# kf.split(X_train)으로 추출된 학습과 검증 index값으로 학습과 검증 데이터 세트 분리
X_tr, y_tr = X_train.iloc[tr_index], y_train.iloc[tr_index]
X_val, y_val = X_train.iloc[val_index], y_train.iloc[val_index]
# early stopping은 30회로 설정하고 추출된 학습과 검증 데이터로 XGBClassifier 학습 수행.
xgb_clf.fit(X_tr, y_tr, early_stopping_rounds=30, eval_metric='auc'
, eval_set=[(X_tr, y_tr), (X_val, y_val)])
# 1로 예측한 확률값 추출후 roc auc 계산하고 평균 roc auc 계산을 위해 list에 결과값 담음.
score = roc_auc_score(y_val, xgb_clf.predict_proba(X_val)[:, 1])
roc_auc_list.append(score)
# 3개 k-fold로 계산된 roc_auc값의 평균값을 반환하되,
# HyperOpt는 목적함수의 최소값을 위한 입력값을 찾으므로 -1을 곱한 뒤 반환.
return -1 * np.mean(roc_auc_list) 이제 HyperOpt를 이용하여 하이퍼 파라미터 튜닝을 수행할 것이다.
하이퍼 파라미터 검색 공간 설정
lgbm_search_space = {
'num_leaves':hp.quniform('num_leaves', 32, 64, 1),
'max_depth' : hp.quniform('max_depth', 100, 160, 1),
'min_child_samples':hp.quniform('min_child_samples', 60, 100, 1),
'subsample' : hp.uniform('subsample', 0.7, 1),
'learning_rate':hp.uniform('learning_rate', 0.01, 0.2)
}fmin()을 호출하여 최적 하이퍼 파라미터 도출
import numpy as np
from hyperopt import fmin, tpe, Trials
# fmin()호출하여 최적 하이퍼파라미터를 도출
trials = Trials()
# fmin() 함수를 호출하고 max_evals 회수만큼 반복 후 목적함수의 최소값을 가지는 최적 입력값 추출
best = fmin(fn=objective_func,
space=lgbm_search_space,
algo=tpe.suggest,
max_evals=50,
trials=trials,
rstate=np.random.default_rng(seed=30))
print('best: ', best)[0] validation_0-auc:0.50000 validation_1-auc:0.50000
[1] validation_0-auc:0.50000 validation_1-auc:0.50000
[2] validation_0-auc:0.50000 validation_1-auc:0.50000
[3] validation_0-auc:0.50000 validation_1-auc:0.50000
[4] validation_0-auc:0.50000 validation_1-auc:0.50000
[5] validation_0-auc:0.50000 validation_1-auc:0.50000
[6] validation_0-auc:0.50000 validation_1-auc:0.50000
[7] validation_0-auc:0.50000 validation_1-auc:0.50000
[8] validation_0-auc:0.50000 validation_1-auc:0.50000
[9] validation_0-auc:0.50000 validation_1-auc:0.50000
[10] validation_0-auc:0.50000 validation_1-auc:0.50000
[11] validation_0-auc:0.50000 validation_1-auc:0.50000
[12] validation_0-auc:0.50000 validation_1-auc:0.50000
[13] validation_0-auc:0.50000 validation_1-auc:0.50000
[14] validation_0-auc:0.50000 validation_1-auc:0.50000
[15] validation_0-auc:0.50000 validation_1-auc:0.50000
[16] validation_0-auc:0.50000 validation_1-auc:0.50000
[17] validation_0-auc:0.50000 validation_1-auc:0.50000
[18] validation_0-auc:0.50000 validation_1-auc:0.50000
[19] validation_0-auc:0.50000 validation_1-auc:0.50000
[20] validation_0-auc:0.50000 validation_1-auc:0.50000
[21] validation_0-auc:0.50000 validation_1-auc:0.50000
[22] validation_0-auc:0.50000 validation_1-auc:0.50000
[23] validation_0-auc:0.50000 validation_1-auc:0.50000
[24] validation_0-auc:0.50000 validation_1-auc:0.50000
[25] validation_0-auc:0.50000 validation_1-auc:0.50000
[26] validation_0-auc:0.50000 validation_1-auc:0.50000
[27] validation_0-auc:0.50000 validation_1-auc:0.50000
[28] validation_0-auc:0.50000 validation_1-auc:0.50000
[29] validation_0-auc:0.50000 validation_1-auc:0.50000
[30] validation_0-auc:0.50000 validation_1-auc:0.50000
0%| | 0/50 [00:06<?, ?trial/s, best loss=?]
...
이하 생략
best: {'learning_rate': 0.02347777899863792, 'max_depth': 134.0, 'min_child_samples': 75.0, 'num_leaves': 34.0, 'subsample': 0.7754775757159653}출력된 하이퍼 파라미터를 이용하여 LightGBM학습 후 Test Data Set에서 ROC-AUC를 평가해본다
lgbm_clf = LGBMClassifier(n_estimators=500,
num_leaves=int(best['num_leaves']),
max_dept=int(best['max_depth']),
min_child_samples=int(best['min_child_samples']),
subsample=round(best['subsample'], 5),
learning_rate=round(best['learning_rate'], 5)
)
# evaluation metric를 auc로, early stopping은 100으로 설정하고 학습 수행
lgbm_clf.fit(X_tr, y_tr, early_stopping_rounds=100, eval_metric="auc", eval_set=[(X_tr, y_tr), (X_val, y_val)])
lgbm_roc_score = roc_auc_score(y_test, xgb_clf.predict_proba(X_test)[:,1])
print(f'ROC-AUC : {lgbm_roc_score}')ROC-AUC : 0.5LightGBM의 경우 학습시간이 상대적으로 빠르기 때문에 위에 기술된 하이퍼 파라미터 외에 추가적으로 튜닝을 수행해보는 것도 좋을거 같다.