복습문제
# 빈칸에 알맞은 말을 적으세요
# LightGBM의 한가지 단점으로 알려진 것은 적은 데이터 셋에 적용할 경우 __이 발생하기 쉽다는 것이다
과적합
# XGMoost는 LightGBM에 비하여 과적화될 확률이 높다(ox)
O
# training set를 training/validation split를 한 이유는 무엇잇가요
학습 조기 중단을 하기 위하여
[출제자 답변]
과적합을 피하기 위하여
# HyperOpt를 사용할 때 다음 보기를 순서대로 나열하세요
# a. 함수설정
# b. 범위설정
# c. fmin()으로 xy값 찾기
b-a-c
# 다음중 랜덤 포레스트의 설명으로 옳지 않은 것은
# 1) 가지를 나눌 때마다 p개의 변수 중 랜덤하게 m개의 변수만 고려한다
# 2) 소수의 변수에 대한 상관성이나 원소가 가진 영향력을 제거할 수 있다
# 3) 원본 데이터의 건수가 200개일 때 10개의 결정 트리 기반으로 학습하려고 하면 20개씩 10개의 데이터 건수로 나눈다
# 4) 여러개의 데어터 셋을 분할 할때 부트스트래핑(bootstrapping) 분할 방식을 이용하며, 이는 중첩(복원)을 허용한다.
3 - 중복 추출을 허용하기 때문에 이런식으로 나눌 수는 없다
# 다음은 수업중 XGB모델을 구현하기 위한 코드 중 일부이다
X_train, X_test, y_train, y_test = train_test_split(X_features, y_label, test_size=0.2, random_state=11)
X_tr, X_val, y_tr, y_val = train_test_split(X_train, y_train, test_size=0.3, random_state=11)
# 원본 데이터는 몇 조각으로 나뉘어졌는가
6
# hyperopt의 hp 모듈을 사용하여 -20~20까지의 2간격을 가지는 입력변수와 x와
#-15~15까지 1 간격으로 입력변수 y를 설정하세요
from hyperopt import hp
search_space ={'x' : hp.quniform('x', -20, 20, 2) , 'y' : hp.quniform('y', -15, 15, 1)}
# LightGBM이 XGB 대비 나은 점 두가지는 무엇인가요
학습시간이 빠르다
더 적은 메모리를 사용한다
# hyperopt를 사용할 때 목적함수의 반환값들을 어떤 클래스 객체로 저장하는가.
Trials()
# LightGBM은 최대한 균형잡힌 트리를 유지하면서 분할하기 때문에 트리의 깊이가 최소화될수 있다
x - 불균형하게 트리를 만들기 때문에 깊이가 엄청 깊어질 위험이 있다.
# HyperOpt는 목적함수 반환값의 최대값을 가지는 최적 입력값을 유추한다
x - 최소값
# 틀린것을 모두 고르세요
# 1. LightGBM은 XGB보다 학습에 걸리는 시간이 훨씬 적다
# 2. LightGBM은 XGB와 예측 성능에 별 차이가 없다
# 3. LightGBM은 적은 데이터 셋에 적용할 경우 과적합 위험이 크다
# 4. LightGBM은 균형 트리 분할 방식을 사용한다
# 5. LightGBM은 다른 모델에 비해 단순하다는 장점이 있다.
4, 5
# LightGBM의 파라미터 max_depth의 default값은?
-1
# LightGBM에서 max_depth값을 따로 지정하지 않을경우 어떤 의미를 가지는가?
트리 깊이에 제한이 없다.
# 사이킷 런 분류 알고리즘에서 각 label데이터의 확률을 보여주는 메서드는 무엇인가요?
predict_proba
# ROC곡선이 가운데 직선에 가까울 수록 성능이 떨어지며, 멀어질 수록 성능이 뛰어나다(ox)
o
# 분류 결정 임계값이 높아질수록 Positive로 예측할 확률이 높아진다(ox)
x
# 보기에서 틀린것을 고르세요
# 1) 정밀도가 중요한 경우, 음성을 양성으로 잘못 판단하면 큰 영향이 발생한다
# 2) TP/(TP+FP)는 정밀도의 공식이다
# 3) True Positive Rate는 재현율이다
# 4) 전체 환자를 Positive라 예측하고 실제 양성인 환자가 n명이라면 재현율은 0이 된다.
# 5) 전체 환자중 1명만 Positive라 예측하고 나머지를 전부 Negative라 예측하면 정밀도는 1이 된다.
4
# 오차 행렬의 원소값을 이용하여 정밀도, 재현율(민감도), 특이도에 대한 수식을 쓰세요
정밀도 = TP / (TP + FP)
재현율(recall, sensitivity, TPR) = TP / (TP + FN)
특이성 = TN / (FP + TN)
# mpg데이터를 불러오세요
import pydataset
mpg = pydataset.data('mpg')
# 아래 명령문을 시행하세요
from collections import Counter
Counter(mpg.fl)
# Counter({'p': 52, 'r': 168, 'e': 8, 'd': 5, 'c': 1})
# 연료 종류(fl) 중 edc의 개수가 너무 적어 이를 삭제하고 p, r 종류만 레이블 값으로 두려고 한다.
# 연료 종류가 e d c인 행은 삭제하세요
mpg.drop(index = mpg[mpg['fl'] == 'e'].index, inplace=True)
mpg.drop(index = mpg[mpg['fl'] == 'd'].index, inplace=True)
mpg.drop(index = mpg[mpg['fl'] == 'c'].index, inplace=True)
mpg['fl'].value_counts()
# [추가 답변]
mpg['fl'].replace(['e', 'd', 'c'], np.nan, inplace = True)
mpg['fl'].dropna()
# [추가 답변]
mpg.loc[(mpg.fl == 'p' | (mpg.fl == 'r')]
# 피처와 레이블로 분리해주세요
X_features = mpg.drop(['fl'], axis = 1)
y_labels = mpg['fl']
# 정보 확인
X_features.info()
# <class 'pandas.core.frame.DataFrame'>
# Int64Index: 220 entries, 1 to 234
# Data columns (total 10 columns):
# # Column Non-Null Count Dtype
# --- ------ -------------- -----
# 0 manufacturer 220 non-null object
# 1 model 220 non-null object
# 2 displ 220 non-null float64
# 3 year 220 non-null int64
# 4 cyl 220 non-null int64
# 5 trans 220 non-null object
# 6 drv 220 non-null object
# 7 cty 220 non-null int64
# 8 hwy 220 non-null int64
# 9 class 220 non-null object
# dtypes: float64(1), int64(4), object(5)
# memory usage: 18.9+ KB
# 현재 피처와 레이블에 문자열이 존재한다. 이를 레이블 인코딩 하세요
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
y_labels = encoder.fit_transform(y_labels)
y_labels
columns = X_features.columns
for column in ['manufacturer', 'model', 'trans', 'drv', 'class']:
X_features[column] = encoder.fit_transform(X_features[column])
X_features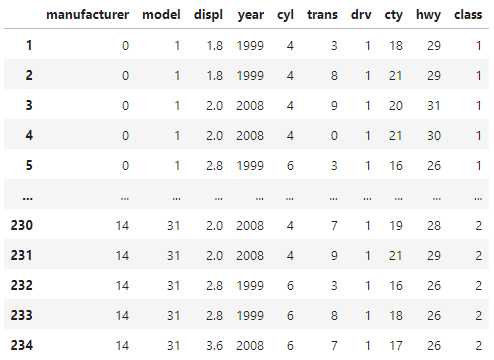
# 정제한 데이터를 5구간으로 나눈뒤, 정확도를 사용하여 평가하시오
# cross_val_scroe() 사용, classifier는 DecisionTree
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeClassifier
import numpy as np
dt_clf = DecisionTreeClassifier()
scores = cross_val_score(dt_clf, X_features, y_labels, scoring = 'accuracy', cv = 5)
print(f'정확도 : {np.mean(scores)}')
# 정확도 : 0.6954545454545455 위키북스의 '파이썬 머신러닝 완벅 가이드' 개정 2판으로 공부하고 있습니다. 실습 과정과 이해에 따라 내용의 누락 및 코드의 변형이 있을 수 있습니다.
언더 샘플링과 오버 샘플링의 이해
레이블이 불균형한 분포를 가진 Data set를 학습 시킬 때 예측성능의 문제가 발생할 수 있다. 이상 레이블을 가지는 데이터 건수가 매우 적기 때문에 제대로 다양한 유형을 학습하지 못하는 반면 정상 레이블을 가지는 데이터 건수가 매우 많기 때문에 생기는 문제이다. 그렇기 때문에 적절한 학습 데이터를 확보하는 방안이 필요한데, 대표적인 방안으로는 언더 샘플링과 오버 샘플링이 있다.
언더 샘플링
- 많은 데이터 셋을 적은 데이터 셋 수준으로 감소시키는 방식
- 정상 레이블이 10,000건, 이상레이블이 100 건이라면 정상 레이블 데이터도 100건으로 줄여버린다
- 과도하게 정상 레이블로 학습/예측하는 부작용은 개선되었지만 과도한 데이터 감소로 오히려 정상 레이블의 제대로된 학습 수행이 어려울 수 있다.
오버 샘플링
- 예측 성능상 더 유리한 경우가 많아 주로 사용된다
- 적은 데이터 셋을 많은 데이터 셋 수준으로 증가하여 맞추는 방식
- 단순히 동일 데이터를 증식한다면 과적합 될 수 있기 때문에, 원본 데이터 피처값을 약간 변경하며 증식한다
- 대표적으로는 SMOTE(Synthetic Minority Over-sampling Technique) 방법이 있다
- SMOTE 는 적은 데이터 셋에 있는 개별 데이터들의 K최근접 이웃(KNN)을 찾아 데이터와 K개의 이웃들 차이를 일정 값으로 만들어 기존 데이터와 약간의 차이가 나는 새로운 데이터들을 생성하는 방식이다.
분류 실습 - 캐글 신용카드 사기 검출
import pandas as pd
import numpy as np
# 읽어오기
card_df = pd.read_csv("./creditcard.csv/creditcard.csv")
card_df[:3]
card_df.shape(284807, 31)데이터 셋 분리
# 데이터 셋 분리
from sklearn.model_selection import train_test_split
X_features = card_df.iloc[:,:-1]
y_lables = card_df.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X_features, y_lables, test_size=0.3, random_state=0, stratify=y_lables)
# 나눠진 데이터 셋트들의 비율을 서로 환산하여 분할 비율 확인
print('학습데이터 레이블 값 비율')
print(y_train.value_counts()/len(y_train))
print()
print('테스트 데이터 레이블 값 비율')
print(y_test.value_counts()/len(y_test))학습데이터 레이블 값 비율
0 0.998275
1 0.001725
Name: Class, dtype: float64
테스트 데이터 레이블 값 비율
0 0.998268
1 0.001732
Name: Class, dtype: float64학습 데이터와 테스트 데이터의 1값이 약 0.0017로 큰차이없이 분할된것을 확인해 볼 수 있다.
+) train_test_split의 stratify
- default=None
- classification을 다룰 때 매우 중요한 옵션값이다. stratify 값을 target으로 지정해주면 각각의 class 비율(ratio)을 train / validation에 유지해 줌. (한 쪽에 쏠려서 분배되는 것을 방지하는 것이다) 만약 이 옵션을 지정해 주지 않고 classification 문제를 다룬다면, 성능의 차이가 많이 날 수도 있다 함.
로지스틱 회귀
먼저 로지스틱 회귀를 이용하여 사기 여부를 예측해보겠다. 성능 평가는 전에 정의했던 사용자 함수 get_clf_eval() 함수를 다시 사용
# 모델 생성
from sklearn.linear_model import LogisticRegression
lr_clf = LogisticRegression(max_iter = 1000)
# 학습/예측
lr_clf.fit(X_train, y_train)
preds = lr_clf.predict(X_test)
# output이 두개가 나오는데 뒤( =1값 =positive값)만 취하겠다.
lr_pred_proba = lr_clf.predict_proba(X_test)[:,1]
# 성능 평가 사용자 정의함수
from sklearn.metrics import roc_auc_score, confusion_matrix, accuracy_score, precision_score, recall_score, f1_score
def get_clf_eval(y_test, pred=None, pred_proba=None):
confusion = confusion_matrix( y_test, pred)
accuracy = accuracy_score(y_test , pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
f1 = f1_score(y_test,pred)
# ROC-AUC 추가
roc_auc = roc_auc_score(y_test, pred_proba)
print('오차 행렬')
print(confusion, '\n')
# ROC-AUC print 추가
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f},\
F1: {3:.4f}, AUC:{4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))
# 평가
get_clf_eval(y_test, preds, lr_pred_proba)오차 행렬
[[85281 14]
[ 57 91]]
정확도: 0.9992, 정밀도: 0.8667, 재현율: 0.6149, F1: 0.7194, AUC:0.9702LGBMClassifier
이번에는 LGBMClassifier를 이용하여 모델을 학습한 뒤 별도의 테스트 데이터셋에서 예측 평가를 수행해보자
# 모델 생성, fit, predict, evaluate
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
lgbm_clf.fit(X_train, y_train)
preds = lgbm_clf.predict(X_test)
lgbm_pred_proba = lgbm_clf.predict_proba(X_test)[:,1]
# 오차행렬, 정확도, 정밀도, 재현율, f1, auc
get_clf_eval(y_test, preds, lgbm_pred_proba)오차 행렬
[[85290 5]
[ 36 112]]
정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790로지스틱 회기에 비해서는 LGBM의 성능이 전체적으로 더 좋게 측정되었다.
추가적으로 데이터 정제 후 적용
이번에는 왜곡된 분포도를 가지는 데이터를 재가공한 뒤에 모델을 다시 테스트 해보자. 위에서 사용했던 로지스틱 회귀의 경우 선형 모델이고, 대부분의 선형모델은 중요 피처값이 정규 분포 형태를 유지하는 것을 선호한다.
표준 정규분포 형태로 변환
Amount 피처는 신용 카드 사용 금액으로 정상/사기 트랜잭션을 결정하는 매우 중요한 속성일 가능성이 높으니 분포도를 확인해보자
card_df['Amount'].describe()count 284807.000000
mean 88.349619
std 250.120109
min 0.000000
25% 5.600000
50% 22.000000
75% 77.165000
max 25691.160000
Name: Amount, dtype: float64시각화로 알아보기
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 4))
plt.xticks(range(0, 30000, 1000), rotation=60)
sns.histplot(card_df['Amount'], bins=100, kde=True)
plt.show()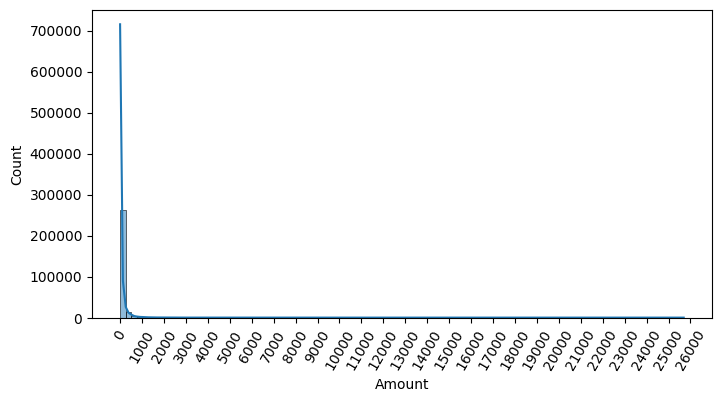
카드 사용 금액이 1000불 이하인 데이터가 대부분인 것이 한눈에 확인된다. Amount를 표준 정규 분포 형태로 변한한 뒤에 로지스틱 회귀의 예측 성능을 측정해보자.
# 표준화 하기
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
card_df['Amount'] = scaler.fit_transform(card_df['Amount'].values.reshape(-1, 1))
card_df['Amount']0 0.244964
1 -0.342475
2 1.160686
3 0.140534
4 -0.073403
...
284802 -0.350151
284803 -0.254117
284804 -0.081839
284805 -0.313249
284806 0.514355
Name: Amount, Length: 284807, dtype: float64# 표준화 결과 평균이 0-분산이 1에 가까운 정규 분포형태가 되었는지 확인
print(f"평균\n{card_df['Amount'].mean()}")
print(f"분산\n{card_df['Amount'].var()}")평균
-1.5966860045099457e-17
분산
1.000003511161984로지스틱회귀와 LightGBM으로 학습/예측 후 사용자 정의 함수로 평가를 진행해보자
# 데이터 셋 분리
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_features, y_lables, test_size=0.3, random_state=0, stratify=y_lables)
# 로지스틱 회귀 예측
lr_clf = LogisticRegression(max_iter = 1000)
lr_clf.fit(X_train, y_train)
preds = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:,1]
# 평가
print('로지스틱 회귀 예측')
get_clf_eval(y_test, preds, lr_pred_proba)
# LightGBM 예측 성능
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
lgbm_clf.fit(X_train, y_train)
preds = lgbm_clf.predict(X_test)
lgbm_pred_proba = lgbm_clf.predict_proba(X_test)[:,1]
# 평가
print('\nLightGBM 예측 성능')
get_clf_eval(y_test, preds, lgbm_pred_proba)로지스틱 회귀 예측
오차 행렬
[[85281 14]
[ 57 91]]
정확도: 0.9992, 정밀도: 0.8667, 재현율: 0.6149, F1: 0.7194, AUC:0.9702
LightGBM 예측 성능
오차 행렬
[[85290 5]
[ 36 112]]
정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790변환 전 수치
로지스틱 회귀 예측
[정확도: 0.9992, 정밀도: 0.8667, 재현율: 0.6149, F1: 0.7194, AUC:0.9702]
LightGBM 예측 성능
[정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790]위와 같았음으로 정말 큰차이가 안보이는 것을 확인할 수 있다. 안보이는 정도가 아니라 값이 같다
로그 변환 후 적용
로그 변환은 데이터 분포도가 심하게 왜곡 되어있을 경우 적용하는 중요 기법 중 하나. 원래 값을 log값으로 변환해 작은 값으로 변환하기 때문에 데이터 분포도의 왜곡을 상당 수준 개선해 준다.
card_df_log = pd.read_csv("./creditcard.csv/creditcard.csv")
card_df_log.drop(['Time'], axis=1, inplace=True)
# log 변환하기
# numpy 의 log1p()함수를 이용해 변환해보자
card_df_log['Amount'] = np.log1p(card_df_log['Amount'])
# 데이터 셋 분리
from sklearn.model_selection import train_test_split
X_features = card_df_log.iloc[:,:-1]
y_lables = card_df_log.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X_features, y_lables, test_size=0.3, random_state=0, stratify=y_lables)
# 로지스틱 회귀 예측
lr_clf = LogisticRegression(max_iter = 1000)
lr_clf.fit(X_train, y_train)
preds = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:,1]
# 평가
print('로지스틱 회귀 예측')
get_clf_eval(y_test, preds, lr_pred_proba)
# LightGBM 예측 성능
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
lgbm_clf.fit(X_train, y_train)
preds = lgbm_clf.predict(X_test)
lgbm_pred_proba = lgbm_clf.predict_proba(X_test)[:,1]
# 평가
print('\nLightGBM 예측 성능')
get_clf_eval(y_test, preds, lgbm_pred_proba)로지스틱 회귀 예측
오차 행렬
[[85283 12]
[ 59 89]]
정확도: 0.9992, 정밀도: 0.8812, 재현율: 0.6014, F1: 0.7149, AUC:0.9727
LightGBM 예측 성능
오차 행렬
[[85290 5]
[ 36 112]]
정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790변환 전 수치
로지스틱 회귀 예측
[정확도: 0.9992, 정밀도: 0.8667, 재현율: 0.6149, F1: 0.7194, AUC:0.9702]
LightGBM 예측 성능
[정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790]로지스틱의 경우 정밀도와 AUC는 조금 향상되었으나 재현율은 저하된 모습.
LightGBM의 경우는 변환전과 후가 같은 결과를 보이고 있다.
이상치 제거 후 적용
이상치를 찾는 방법은 여러가지가 있지만 이중에서 IQR(Inter Quantile Range) 방식을 적용한다. 모든 피처들의 이상치를 검출하는 것은 시간이 많이 소모되며, 결정값과 상관성이 높지 않은 피처들의 경우는 이상치를 제거하더라고 크게 성능 향상에 기여하지 않기 때문에 결정값(즉 레이블)과 가장 상관성이 높은 피처들을 위추로 이상치를 검출하는 것이 좋다.
card_df_iqr = pd.read_csv("./creditcard.csv/creditcard.csv")
card_df_iqr.drop(['Time'], axis=1, inplace=True)
card_df_iqr[:3]DataFrame의 corr()을 이용해 각 피처별로 상관도를 구한 뒤 heatmap 시각화 해보자. 양이 상관도가 높을수록 파란색에 가까우며, 음의 상관관계가 높을 수록 붉은 색에 가깝다.
corr_M = card_df_iqr.corr()
sns.heatmap(corr_M, cmap="RdBu")
plt.show()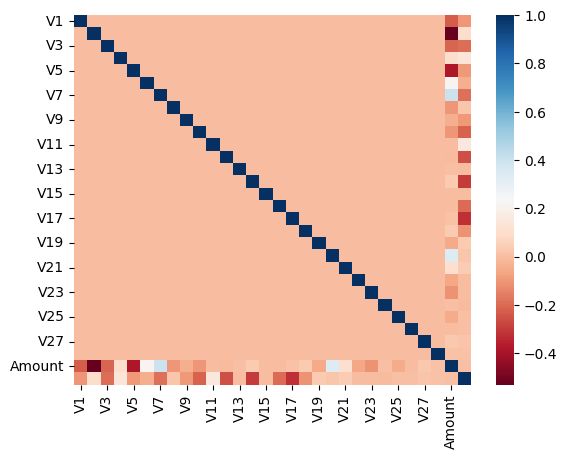
히트맵을 보면 음의 상관관계가 가장 높은 것이 v14와 v17로 나왔고 이중 v14에 대해서만 이상치를 찾아 제거해보도록 하자.
# class 가 1인 경우에만 진행할 것이기 때문에 솎아준다.
fraud = card_df_iqr[card_df_iqr['Class'] == 1]
fraud
IQR 구하기
# 넘파이 함수를 이용해 1/4분위와 3/4분위를 구하고, 이에 기반하여 IQR을 계산한다.
Q_25 = np.percentile(fraud.V14, 25)
Q_75 = np.percentile(fraud.V14, 75)
IQR = Q_75 -Q_25
IQR
# 5.409902115485521
# 또 다르게 IQR 계산하기
Q_25 = fraud['V14'].quantile(.25)
Q_75 = fraud['V14'].quantile(.75)
IQR = Q_75 - Q_25
IQR
# 5.409902115485521
# 구해진 IQR에 1.5를 곱해 최대값과 최소값 지점 구하기
upper_out = Q_75 + 1.5 * IQR
under_out = Q_25 - 1.5 * IQR
# 이상치 데이터 검색
cond1 = fraud['V14'] >= upper_out
cond2 = fraud['V14'] <= under_out
fraud.V14[cond1 | cond2]8296 -19.214325
8615 -18.822087
9035 -18.493773
9252 -18.049998
Name: V14, dtype: float64이상치의 데이터 인덱스 담아주기
temp = fraud.V14[cond1 | cond2].index
tempInt64Index([8296, 8615, 9035, 9252], dtype='int64')card_df_iqr.shape(284807, 30)# card_df에서 이상치를 제거해주세요
card_df_iqr.drop(labels = temp, axis = 0, inplace=True)
card_df_iqr.shape(284803, 30)제거 전 'shape (284807, 30)'에서 이상치 4개 제거하니 'shape (284803, 30)' 로 잘 사라진 것을 확인할 수 있다.
# 데이터 셋 분리
from sklearn.model_selection import train_test_split
X_features = card_df_iqr.iloc[:,:-1]
y_lables = card_df_iqr.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X_features, y_lables, test_size=0.3, random_state=0, stratify=y_lables)
# 로지스틱 회귀 예측
lr_clf = LogisticRegression(max_iter = 1000)
lr_clf.fit(X_train, y_train)
preds = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:,1]
# 평가
print('로지스틱 회귀 예측')
get_clf_eval(y_test, preds, lr_pred_proba)
# LightGBM 예측 성능
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
lgbm_clf.fit(X_train, y_train)
preds = lgbm_clf.predict(X_test)
lgbm_pred_proba = lgbm_clf.predict_proba(X_test)[:,1]
# 평가
print('\nLightGBM 예측 성능')
get_clf_eval(y_test, preds, lgbm_pred_proba)로지스틱 회귀 예측
오차 행렬
[[85279 16]
[ 48 98]]
정확도: 0.9993, 정밀도: 0.8596, 재현율: 0.6712, F1: 0.7538, AUC:0.9739
LightGBM 예측 성능
오차 행렬
[[85291 4]
[ 25 121]]
정확도: 0.9997, 정밀도: 0.9680, 재현율: 0.8288, F1: 0.8930, AUC:0.9791변환 전 수치와 비교하여
로지스틱 회귀 예측
[정확도: 0.9992, 정밀도: 0.8667, 재현율: 0.6149, F1: 0.7194, AUC:0.9702]
LightGBM 예측 성능
[정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790]로지스틱의 경우 정확도와 재현율, f1, auc 가 향상 되었으나 정밀도는 조금 떨어진 모습
LightGBM의 경우 5가지 모두 전반적으로 향상된 모습을 확인 가능
log와 이상치 제거를 함께 한다면?
# card_df_iqr 데이터에 log 적용
card_df_iqr['Amount'] = np.log1p(card_df_iqr['Amount'])
# 데이터 셋 분리
from sklearn.model_selection import train_test_split
X_features = card_df_iqr.iloc[:,:-1]
y_lables = card_df_iqr.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X_features, y_lables, test_size=0.3, random_state=0, stratify=y_lables)
# 로지스틱 회귀 예측
lr_clf = LogisticRegression(max_iter = 1000)
lr_clf.fit(X_train, y_train)
preds = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:,1]
# 평가
print('로지스틱 회귀 예측')
get_clf_eval(y_test, preds, lr_pred_proba)
# LightGBM 예측 성능
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
lgbm_clf.fit(X_train, y_train)
preds = lgbm_clf.predict(X_test)
lgbm_pred_proba = lgbm_clf.predict_proba(X_test)[:,1]
# 평가
print('\nLightGBM 예측 성능')
get_clf_eval(y_test, preds, lgbm_pred_proba)로지스틱 회귀 예측
오차 행렬
[[85281 14]
[ 48 98]]
정확도: 0.9993, 정밀도: 0.8750, 재현율: 0.6712, F1: 0.7597, AUC:0.9743
LightGBM 예측 성능
오차 행렬
[[85291 4]
[ 25 121]]
정확도: 0.9997, 정밀도: 0.9680, 재현율: 0.8288, F1: 0.8930, AUC:0.9791이상치 제거만 했을 때는 아래와 같았다.
로지스틱 회귀 예측
[정확도: 0.9993, 정밀도: 0.8596, 재현율: 0.6712, F1: 0.7538, AUC:0.9739]
LightGBM 예측 성능
[정확도: 0.9997, 정밀도: 0.9680, 재현율: 0.8288, F1: 0.8930, AUC:0.9791]함께 했을 때.. 로지스틱의 경우 정밀도와 f1, auc가 향상되었다.
LightGBM의 경우변화가 없는 모습.
성능이 떨어지지는 않았으니 같이 하는 것이 나쁘지는 않은 선택같이 보이는 결과를 주었다.
SMOTE 오버 샘플링 적용
SMOTE를 적용할 때에는 반드시 학습 데이터 셋만 오버 샘플링을 해야한다. 검증 데이터 셋이나 테스트 데이터 셋을 오버 샘플링할 경우 결국은 원본 데이터 세트가 아닌 데이터 세트에서 검증 또는 테스트를 수행하기 때문에 올바른 검증/테스트가 될수 없기 때문이다.
패키지 설치
# SMOTE를 구현한 대표적인 파이썬 패키지 설치
!pip install imbalanced-learn데이터 증식
from imblearn.over_sampling import SMOTE
# test는 건드리면 안된다. 따라서 train만 건드리기
smote = SMOTE(random_state=0)
X_train_smote, y_train_smote = smote.fit_resample(X_train, y_train)
print(f'SMOTE 적용전 학습용 피처/레이블 데이터 셋 : {X_train.shape}, {y_train.shape}')
print(f'SMOTE 적용후 학습용 피처/레이블 데이터 셋 : {X_train_smote.shape}, {y_train_smote.shape}')
print(f'SMOTE 적용후 레이블 값 분포 : \n{pd.Series(y_train_smote).value_counts()}')SMOTE 적용전 학습용 피처/레이블 데이터 셋 : (199362, 29), (199362,)
SMOTE 적용후 학습용 피처/레이블 데이터 셋 : (398040, 29), (398040,)
SMOTE 적용후 레이블 값 분포 :
0 199020
1 199020
Name: Class, dtype: int64SMOTE 오버 샘플링 이후 데이터가 대략 2배 정도 증가한 모습이며, 레이블 값의 0과 1의 분포가 동일하게 생성된 모습을 확인할 수 있다.
# 로지스틱 회귀 예측
lr_clf = LogisticRegression(max_iter = 1000)
lr_clf.fit(X_train, y_train)
preds = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:,1]
# 평가
print('로지스틱 회귀 예측')
get_clf_eval(y_test, preds, lr_pred_proba)
# LightGBM 예측 성능
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
lgbm_clf.fit(X_train, y_train)
preds = lgbm_clf.predict(X_test)
lgbm_pred_proba = lgbm_clf.predict_proba(X_test)[:,1]
# 평가
print('\nLightGBM 예측 성능')
get_clf_eval(y_test, preds, lgbm_pred_proba)로지스틱 회귀 예측
오차 행렬
[[85281 14]
[ 48 98]]
정확도: 0.9993, 정밀도: 0.8750, 재현율: 0.6712, F1: 0.7597, AUC:0.9743
LightGBM 예측 성능
오차 행렬
[[85291 4]
[ 25 121]]
정확도: 0.9997, 정밀도: 0.9680, 재현율: 0.8288, F1: 0.8930, AUC:0.9791SMOTE 이전 수치는 아래와 같았는데
로지스틱 회귀 예측
[정확도: 0.9992, 정밀도: 0.8667, 재현율: 0.6149, F1: 0.7194, AUC:0.9702]
LightGBM 예측 성능
[정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453, AUC:0.9790]로지스틱의 경우 전체적으로 조금씩 향상되었고, LightGBM의 경우에도 전체적으로 조금씩 향상된 모습을 보였다.
boost_from_average=Ture
레이블값이 극도로 불균형한 경우 boost_from_average=Ture로 설정할 경우 성능이 저하된다고 하여 테스트 해봤다.
# 반복적으로 쓰이고 있으니 사용자 함수로 정의
def get_model_train_eval(model, train_x=None, test_x=None, train_y=None, test_y=None):
model.fit(train_x, train_y)
pred = model.predict(test_x)
pred_proba = model.predict_proba(test_x)[:,1]
get_clf_eval(test_y, pred, pred_proba)
print('LightGBM : boost_from_average=True 예측 성능')
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=True)
get_model_train_eval(lgbm_clf, train_x=X_train, test_x=X_test, train_y=y_train, test_y=y_test)
print('\nLightGBM 예측 성능')
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
get_model_train_eval(lgbm_clf, train_x=X_train, test_x=X_test, train_y=y_train, test_y=y_test)LightGBM : boost_from_average=True 예측 성능
오차 행렬
[[85268 27]
[ 36 110]]
정확도: 0.9993, 정밀도: 0.8029, 재현율: 0.7534, F1: 0.7774, AUC:0.9219
LightGBM 예측 성능
오차 행렬
[[85291 4]
[ 25 121]]
정확도: 0.9997, 정밀도: 0.9680, 재현율: 0.8288, F1: 0.8930, AUC:0.9791정말 옵션값만 True / False로 설정해줬을 뿐인데 모든 값에서 값이 떨어진 것을 확인할 수 있었다. 가중치 업데이트 시 평균값에서 시작하게 하는 옵션이라는데 데이터가 불균형하기 때문에 평균값도 올바르지 않아서(? 그런것일까...
LightGBM 2.1.0 이상 버전에서 boost_from_average 파라미터 디폴트 값은 True이기 때문에 데이터 값이 불균형하면 False 로 꺼주는 것을 잊지 말자.
boost_from_average 파라미터 정보 참고 : lightGBM/XGBoost 파라미터 설명
스태킹 앙상블
스태킹(Stacking)은 개별적인 여러 알고리즘을 서로 결합해 예측 결과를 도출한다는 점에서는 앞선 배깅이나 부스팅과 비슷한 점이 있지만, 가장 큰 차이점은 '개별 알고리즘으로 예측한 데이터'를 기반으로 다시 예측을 수행한다는 것이다.
개별 알고리즘으로 예측한 데이터를 메타 데이터 셋으로 만들어 그 데이터를 또 다른 별도의 알고리즘으로 최종 학습을 수행, 테스트를 수행하는 방법이다. 이런식으로 개별 모델의 예측 데이터를 기반으로 학습하고 예측하는 방식을 메타 모델이라고 한다.
현실에서는 잘 적용하지 않는 기법이지만 캐글과 같은 대회처럼 조금이라도 성능 수치를 높이고 싶을 때 사용한다.

2-3개의 개별 모델만을 결합해서는 쉽게 예측 성능을 향상시킬 순 없으며, 스태킹을 적용했다고 하여 반드시 성능 향상이 되리라는 보장도 없다. 일반적으로는 성능이 비슷한 모델을 결합해 좀 더 나은 성능 향상을 도출하기 위해 적용된다.
적용 - 위스콘신 유방암 데이터
데이터 불러오기 및 나누기
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
# 위스콘신 유방암 데이터
cancer_data = load_breast_cancer()
X_data = cancer_data.data
y_label = cancer_data.target
X_train , X_test , y_train , y_test = train_test_split(X_data , y_label , test_size=0.2 , random_state=0)ML 모델 불러오기 및 학습
import pandas as pd
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
cancer = load_breast_cancer()
type(cancer)
# 데이터 처리
X_data = cancer.data
y_label = cancer.target
X_train , X_test , y_train , y_test = train_test_split(X_data , y_label , test_size=0.2 , random_state=0)
# 개별 ML 모델을 위한 Classifier 생성.
knn_clf = KNeighborsClassifier(n_neighbors=4)
rf_clf = RandomForestClassifier(n_estimators=100, random_state=0)
dt_clf = DecisionTreeClassifier()
ada_clf = AdaBoostClassifier(n_estimators=100)
# 개별 모델들을 학습.
knn_clf.fit(X_train, y_train)
rf_clf.fit(X_train , y_train)
dt_clf.fit(X_train , y_train)
ada_clf.fit(X_train, y_train)AdaBoostClassifier(n_estimators=100)KNN, 랜덤 포레스트, 결정 트리, 에이다부스트를 개별 모델로 설정했다. 학습된 개별 모델들이 각자 반환하는 예측 데이터 셋을 생성하고 개별 모델의 정확도 측정.
knn_pred = knn_clf.predict(X_test)
rf_pred = rf_clf.predict(X_test)
dt_pred = dt_clf.predict(X_test)
ada_pred = ada_clf.predict(X_test)
print('KNN 정확도: {0:.4f}'.format(accuracy_score(y_test, knn_pred)))
print('랜덤 포레스트 정확도: {0:.4f}'.format(accuracy_score(y_test, rf_pred)))
print('결정 트리 정확도: {0:.4f}'.format(accuracy_score(y_test, dt_pred)))
print('에이다부스트 정확도: {0:.4f} '.format(accuracy_score(y_test, ada_pred))) KNN 정확도: 0.9211
랜덤 포레스트 정확도: 0.9649
결정 트리 정확도: 0.9123
에이다부스트 정확도: 0.9561이제 개별 예측 결과를 알았으니 이 것들을 하나로 붙여주어야 한다. 옆으로 길게 나와있는 예측값을 세로로 세워서 붙여준다. (위에 그림처럼)
# 개별 예측 결과를 stacking
# 배열화하여 붙여준 결과
pred = np.array([knn_pred, rf_pred, dt_pred, ada_pred])
print(pred.shape)
(4, 114)
# ---------
# ---------
# ---------
# --------- 의 모양으로 붙은것을
# | | |
# | | |
# | | |
# | | | 의 모양으로 전치 시켜준것이다.
pred = pred.T
print(pred.shape)
(114, 4)최종 학습/예측/평가
# 최종 Stacking 모델을 위한 Classifier 생성
# 최종 모델은 로지스틱으로 하기로 했다.
lr_final = LogisticRegression(C=10)
lr_final.fit(pred, y_test)
final = lr_final.predict(pred)
accuracy_score(y_test, final)0.9736842105263158LogisticRegression뒤에 C는 하이퍼 파라미터를 제어하는 옵션인데, 높은 값을 설정할 수록 낮은 강도의 제약조건이 설정되고 낮은 값을 설정할 수록 높은 강도의 제작조건이 설정된다.
LogisticRegression(C조건)
차이가 궁금했기에 적용해보기로 한다.
lr_final = LogisticRegression(C=0.01).fit(pred, y_test)
final_001 = lr_final.predict(pred)
lr_final = LogisticRegression(C=0.1).fit(pred, y_test)
final_01 = lr_final.predict(pred)
lr_final = LogisticRegression(C=1).fit(pred, y_test)
final_1 = lr_final.predict(pred)
lr_final = LogisticRegression(C=10).fit(pred, y_test)
final_10 = lr_final.predict(pred)
lr_final = LogisticRegression(C=100).fit(pred, y_test)
final_100 = lr_final.predict(pred)
print(f'(C=0.01) : {accuracy_score(y_test, final_001)}')
print(f'(C=0.1) : {accuracy_score(y_test, final_01)}')
print(f'(C=1) : {accuracy_score(y_test, final_1)}')
print(f'(C=10) : {accuracy_score(y_test, final_10)}')
print(f'(C=100) : {accuracy_score(y_test, final_100)}')(C=0.01) : 0.9298245614035088
(C=0.1) : 0.9736842105263158
(C=1) : 0.9736842105263158
(C=10) : 0.9736842105263158
(C=100) : 0.9736842105263158결과를 보면 0.01 보다는 0.01 로 설정했을 때 정확도가 높아진 것을 확인할 수 있었지만, 그 이상으로 높인다고 해서 눈에 띄는 변경이 없었다.
C는 Regularization(정규화)의 강도를 결정하는 parameter이다. 값이 낮을수록 계수를 0으로 근사하므로 regularization이 강화되는 데, 값이 클수록 overfitting의 가능성이 증가한다. 따라서 값을 조정하고 확인하면서 적당한 값을 찾는 것이 중요한 옵션으로 보인다.
spyder 사용해보기
줄 이동 : 움직일 줄 클릭 + alt + 이동할 위치로 이동