복습문제
# 분포가 심하게 왜곡되었을 경우 _변환을 적용하는 것이 좋다
표준화, log
[출제자 답변]
log
# 로지스틱 회귀는 분류알고리즘이다
O
# odds ratio = 오즈비 = 승산비 의 식을 적어주세요
[출제자 답변]
p/1-p
이길 확률 / (이길확률+질확률)
# 주성분을 가진 데이터 세트로 차원축소하는 알고리즘의 이름은?
PCA
# PCA : 데이터 변동성이 가장 (큰/작은) 방향으로 축 생성
큰
# 차원축소법은 '피처 선택'과 '피처 추출'로 나눌수 있다. 피처 선택이란?
불필요한 피처는 아예 제거하고 데이터의 특징을 잘 나타내는 피처만 선택
# 로그 변환할때 사용하는 함수는?
np.log1p()
# 변환한 로그를 다시 지수로 변환하는 함수는?
np.expm1()
# 차원축소를 진행한 이후 원래의 자료로 완벽하게 복구 할 수 있나요?
x - 완벽하게?
# LinearRegression의 output 데이터 타입은?
int, float와 같은 연속형 숫자타입
# LogisticRegression의 output 데이터 타입은?
볌주형
# 회귀 트리 Regressor 클래스는 coef_속성이 없고
대신 feature_importances_를 이용해 피처별 중요도를 알수 있다
o
[출제자 답변]
# 로지스틱 회귀는 0~1사이에서 완만한 S-surve를 그린다. 이 곡선의 이름은?
시그모이드(Sigmoid)
# 머신러닝 결과에 대한 예측확률을 높이기 위해 전처리 작업을 시도하려고 합니다
# 해볼 수 있는 전처리 작업들을 적어주세요
표준화, 정규화, log 변환, 데이터 축소, 데이터 이산화
[출제자 답변]
인코딩(레이블/원핫), 정규화, 표준화, 로그변환, 차원축소, 이상치 제거
# LogisticRaegression클래스의 하이퍼 파라미터 중 'C'값이 작을 수록 규제강도가 크다
o
- 높은 값을 설정할 수록 낮은 강도의 제약조건이 설정
- 낮은 값을 설정할 수록 높은 강도의 제작조건
# PCA(n_componenrs=)에서 n_components의 뜻은?
몇 개의 차원으로 줄일지
import pydataset as py
mpg = py.data('mpg')
# manufacturer은 모두 몇개임니까?
mpg['manufacturer'].value_counts()
# 값이 많은 것들(5개)만 남겨주기
df1 = mpg.query("manufacturer in ['dodge','toyota','volkswagen','ford','chevrolet']")
# 다른방법
a=['dodge','toyota','volkswagen','ford','chevrolet']
mpg[mpg['manufacturer'].isin(a)]
# 또 다른 방법
top5 = mpg['manufacturer'].value_counts()[:5].index
mpg[mpg['manufacturer'].apply(lambda x: x in list(top5))]
# 또 다른 방법
mpg.query('manufacturer in @top5')위키북스의 '파이썬 머신러닝 완벅 가이드' 개정 2판으로 공부하고 있습니다. 실습 과정과 이해에 따라 내용의 누락 및 코드의 변형이 있을 수 있습니다.
LDA(Linear Discriminant Analysis)
선형 판별 분석법으로 불리며 PCA와 매우 유사하지만 비지도 학습인 PCA와는 다르게 LDA는 지도학습이다. 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 유지한다
- PCA : 입력데이터의 변동성이 가장 큰 축을 찾는다. 공분산 행렬을 사용
- LDA : 입력데이터의 결정 값 클래스를 최대한 분리할 수 있는 축을 찾는다. 클래스 간 분산, 클래스 내 분산 행렬을 사용
즉, LDA는 클래스 분리를 최대화 하는 축을 찾기 위해 클래스간 분산은 최대화하고, 클래스 내 분산은 최소화한다.
LDA 수행과정
- 클래스 내부와 클래스 간 분산 행렬을 계산한다. 두 행렬은 입력 데이터의 결정값 클래스 별로 개별 피처의 평균 벡터를 기반하여 구한다.
- 클래스 내부 분산 행렬을 Sw, 클래스간 분산을 SB라 하면 아래와 같이 표현 가능하다.
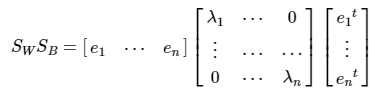
- 고유값이 가장 큰 순으로 K개(LDA변환 차수)만큼 고유 벡터를 추출한다
- 고유값이 가장 큰 순으로 추출된 고유벡터를 이용하여 새롭게 입력 데이터를 변환한다.
구현하며 이해하기
사이킷 런은 LDA를 LinearDiscriminantAnalysis 클래스로 제공한다. 붓꼿 데이터 세트를 로드하여 진행해보겠다.
# LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
# 데이터 불러오고 변수에 할당하기
iris = load_iris()
X_feature = iris.data
y_label = iris.targetStandardScaler()를 이용하여 스케일링
# 표준 정규 분포로 스케일링
scaled = StandardScaler()
X_scaled = scaled.fit_transform(X_feature)2개의 컴포넌트로 데이터를 LDA변환하려 한다. 이때 주의할 점은 LDA는 지도학습이기 때문에 클래스 결정값이 필요하다는 점이다.
# 2개의 컴포넌트로 LDA 변환
lda = LinearDiscriminantAnalysis(n_components=2)
# PCA는 비지도 학습이지만 LDA는 지도 학습이다
# 따라서 클래스 결정값이 변환시 필요하다
# pca라면 [ pca.fit_transform(X_scaled) ]
iris_lda = lda.fit_transform(X_scaled, y_label)
print(iris_lda.shape)(150, 2)SVD(Singular Value Decomposition)
역시나 PCA와 유사한 행렬 분해 기법을 이용한다. 하지만 PCA의 경우는 정방행렬만 고유벡터로 분해할 수 있는 반면, SVD는 정방행렬 뿐 아니라 행과 열의 크기가 다른 행렬에도 적용할 수 있다는 점이 다르다.
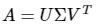
SVD는 m x n 행렬 A를 위와 같이 분해한다
- U : m x m 행렬. 속한 벡터는 특이벡터(Singular Vector)로 서로 직교한다.
- Σ: m x n 행렬로 대각원소(행렬 A의 특이값)만 0이 아니고 나머지 값은 0이다.
- Vt : n x n 행렬로 속한 벡터는 특이벡터(Singular Vector)로 서로 직교한다.
SVD는 특이값 분해로 분리며, 행렬 U와 A에 속한 벡터는 특이벡토(Singular vetor)이다. 모든 특이벡터는 서로 직교하는 성질을 가짐. 즉 Σ0이 위치한 0이 아닌 값이 행렬 A의 특이 값이 되는 것
구현하며 이해해보기
넘파이의 SVD를 이용해 연산을 수행하고, 분해가 어떤식으로 진행되는지 간단한 예제로 확인해보자
넘파이의 svd모듈 가져오기
import numpy as np
from numpy.linalg import svd4 4랜덤 행렬 생성
※ 랜덤 행렬인 이유 : 개별 로우의 의존성을 없애기 위해서 이다.
np.random.seed(121)
a = np.random.randn(4, 4)
print(np.round(a, 3))[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.014 0.63 1.71 -1.327]
[ 0.402 -0.191 1.404 -1.969]]위에서 생성해준 행렬에 SVD를 적용하여 U와 S(Sigma), Vt를 도출해내보자. SVD분해는 numpy.linalg.svd에 파라미터로 원본 행렬을 입력하면 U행렬, Sigma행렬, V 전치 행렬을 반환해준다.
U, Sigma, Vt = svd(a)
print(U.shape, Sigma.shape, Vt.shape, '\n')
print(f'-----U matrix:\n{np.round(U, 3)}')
print(f'-----Sigma value:\n{np.round(Sigma, 3)}')
print(f'-----V transpose matrix:\n{np.round(Vt, 3)}')(4, 4) (4,) (4, 4)
-----U matrix:
[[-0.079 -0.318 0.867 0.376]
[ 0.383 0.787 0.12 0.469]
[ 0.656 0.022 0.357 -0.664]
[ 0.645 -0.529 -0.328 0.444]]
-----Sigma value:
[3.423 2.023 0.463 0.079]
-----V transpose matrix:
[[ 0.041 0.224 0.786 -0.574]
[-0.2 0.562 0.37 0.712]
[-0.778 0.395 -0.333 -0.357]
[-0.593 -0.692 0.366 0.189]]U행렬과 vt행렬이 4x4 행렬로, Sigma의 경우에는 1차원 행렬인 (4,)로 반환되었다.
분해된 이 U, Sigma, Vt를 이용해 다시 원본 행렬로 복원이 가능한지도 확인해보자. 원본 행렬로의 복원은 이들을 내적하면된다. 유의할 점은 시그마의 경우 0이 아닌 값만 1차원으로 추출했으므로 다시 0을 포함한 대칭 행렬로 변환한 뒤에 내적을 수행해야 한다는 점이다.
# Sigma를 다시 (0을 포함한) 대칭 행렬로 변환
Sigma_mat = np.diag(Sigma)
a_1 = np.dot(np.dot(U, Sigma_mat), Vt)
print(np.round(a_1, 3))[[-0.212 -0.285 -0.574 -0.44 ]
[-0.33 1.184 1.615 0.367]
[-0.014 0.63 1.71 -1.327]
[ 0.402 -0.191 1.404 -1.969]]오와 제대로 복원이 되었다. 이번에는 데이터 세트가 로우간 의존성이 있을 경우 어떻게 시그마 겂이 변하고, 이에 따른 차원 축소가 진행 될 수 있는지 알아보자.
# 세번째 로우는 '첫번째 로우+두번째 로우'로
a[2] = a[0]+ a[1]
# 4번째 로우는 첫번째 로우와 같다고 추가
a[3] = a[0]로우간 관계성이 매우 높아진 상황에서 이 데이터를 SVD로 다시 분해해보자
U, Sigma, Vt = svd(a)
print(U.shape, Sigma.shape, Vt.shape, '\n')
print(f'Sigma value:\n{np.round(Sigma, 3)}')(4, 4) (4,) (4, 4)
Sigma value:
[2.663 0.807 0. 0. ]차원은 이전과 같지만 시그마의 값 중 두가지가 0으로 변해버렸다. 이는 선형 독립인 로우 벡터의 개수가 2개라는 의미라고 한다.
Truncated SVD
Truncated SVD 역시 Full SVD를 축약한 방법으로 Σ의 대각원소 중에 상위 몇 개만 추출하는 방식이다. (연산을 수행한 뒤 원본 행렬을 분해한 U, Sigma, Vt행렬을 반환하지 않는다)
그냥 SVD보다도 더욱 차원을 줄인 방식으로 과정 자체는 별 차이가 없다. 인위적으로 더 작은 차원으로 분해하기 때문에 완벽하게 원본 행렬 복구는 불가능하다.
# TruncatedSVD
from sklearn.decomposition import TruncatedSVD, PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
iris = load_iris()
X_feature = iris.data
# 2개의 주요 컴포넌트로 TruncatedSVD 변환
tsvd = TruncatedSVD(n_components=2)
iris_tsvd = tsvd.fit_transform(X_feature)
# 산점도 2차원으로 TruncatedSVD 변환된 데이터 표현. 품종은 색으로 구분
plt.scatter(x=iris_tsvd[:, 0], y=iris_tsvd[:,1], c=iris.target)
plt.xlabel("TruncatedSVDComponent 1")
plt.ylabel("TruncatedSVDComponent 2")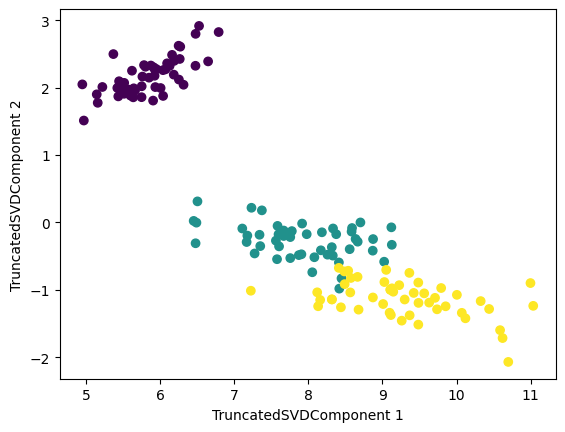
위에서는 스케일링 과정을 하지 않았는데, 차이가 눈에 띄게 있을 지 궁금했다.
# 표준 정규 분포로 스케일링
X_scaled = StandardScaler().fit_transform(X_feature)
# 스케일링 된 데이터를 기반으로 TruncatedSVD 변환 수행
tsvd = TruncatedSVD(n_components=2)
iris_tsvd_sc = tsvd.fit_transform(X_feature)
# 산점도 2차원으로 TruncatedSVD 변환된 데이터 표현. 품종은 색으로 구분
plt.scatter(x=iris_tsvd_sc[:, 0], y=iris_tsvd_sc[:,1], c=iris.target)
plt.xlabel("TruncatedSVDComponent 1")
plt.ylabel("TruncatedSVDComponent 2")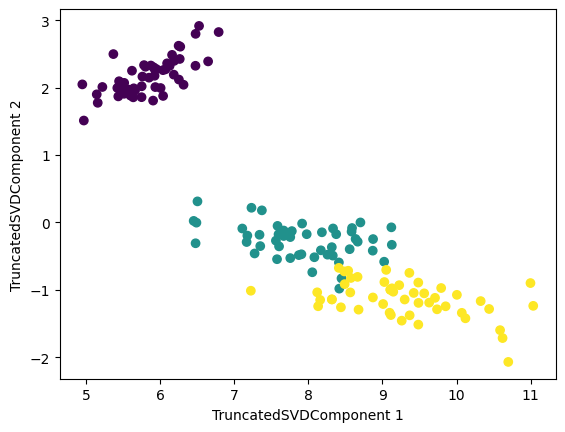
시각화 한 결과만을 봤을 때는 스케일링(표준 정규 분포)을 한 것과 하지 않은 것 사이에 큰 차이가 보이지 않는 것 같았다.
[iris_tsvd_sc == iris_tsvd][array([[False, False],
[False, False],
[ True, False],
[ True, False],
[False, False],
[ True, False],
[False, False],
[ True, False],
[False, False],
[False, False],
[ True, False],
[ True, False],
[False, False],
[ True, False],
[ True, False],
[False, False],그래서 무작정 비교를 하였고 결과는 위와 같이 나오게 되었다. 시각화만 봤을 때는 꽤 같아 보였는데 완전히 같은건 아니구나
사이킷런의 TruncatedSVD와 PCA 클래스 구현을 조금 더 자세히 들여다보면 두 개 클래스 모두 SVD를 이용해 행렬을 분해한다. 시각화를 통해보면 두 개가 거의 동일함을 알 수 있다.
from sklearn.preprocessing import StandardScaler
iris = load_iris()
X_feature = iris.data
y_label = iris.target
# 스케일링
scaler = StandardScaler()
iris_scaled = scaler.fit_transform(X_feature)
# 스케일링 된 데이터를 기반으로 TSVD 변환 수행
tsvd = TruncatedSVD(n_components=2)
iris_tsvd = tsvd.fit_transform(iris_scaled)
# 스케일링 된 데이터를 기반으로 PCA 수행
pca = PCA(n_components=2)
iris_pca = pca.fit_transform(iris_scaled)
# 시각화
# tsvd 변환을 왼쪽에 pca변환으 오른쪽에 표현
fig, (ax1, ax2) = plt.subplots(figsize=(9, 4), ncols=2)
ax1.scatter(x=iris_tsvd[:,0], y=iris_tsvd[:,1], c=iris.target)
ax2.scatter(x=iris_pca[:,0], y=iris_pca[:,1], c=iris.target)
ax1.set_title('TSVD Transformd')
ax2.set_title('PCA Transformed')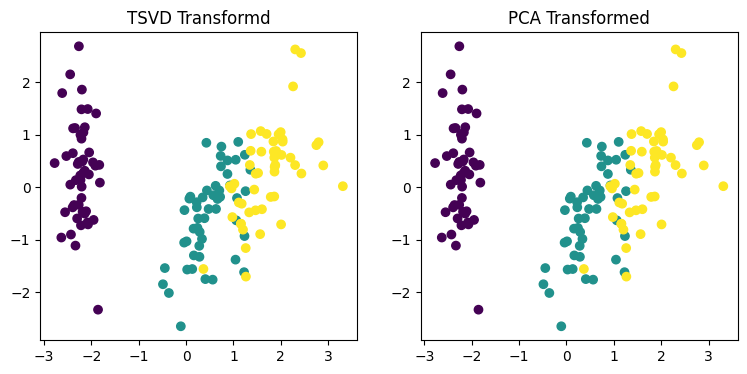
# 두 방법의 컴포넌트 차이 평균
var1 = (iris_pca - iris_tsvd).mean()
print(f"{var1:.3f}")
# 원본 피처별 컴포넌트 비율 차이 평균
var2 = (pca.components_ - tsvd.components_).mean()
print(f"{var2:.3f}")0.000
0.000컴포넌트 값의 차이와 원본 피처별 컴포넌트 비율 값의 차이를 계산해보니 0에 가까운 값으로 두 방법의 결과가 거의 동일함을 알 수 있었다. 즉, 데이터 스케일링을 통해 데이터의 중심이 동일해지면 두 방법은 동일한 변환값을 반환한다.
데이터 세트가 스케일링으로 데이터 중심이 동일해지면 사이킷런의 SVD와 PCA는 동일한 변환을 수행한다. 이는 PCA가 SVD 알고리즘으로 구현되었음을 의미하지만, PCA는 밀집행렬에 대한 변환만 가능하며 SVD는 희소행렬에 대한 변환도 가능하다
NMF(Non-Negative Matrix Factorization)
Truncated SVD와 같이 낮은 랭크를 통한 행렬 근사(Low-Rank Approximation) 방식의 변형이다. 원본 행렬 내의 모든 원소값이 모두 양수라는게 보장되면 두 개의 양수 행렬로 분해 가능하다.
X = WHX가 m x n 행렬이라면 W와 H는 각각 m x p 행렬W, p x n 행렬H 가 되고 여기서 p는 임의의 값으로 상황에 맞게 설정해 줄수 있는 값이다.
예를 들어 [4x6 행렬A]가 있다면
[4x2 행렬W]와 [2x6 행렬H]로 분해할 수 있는 것이다.W는 원본행에 대한 잠재 요소를 특성으로 가지며, H는 원본열에 대한 잠재 요소를 특성으로 가진다.
from sklearn.decomposition import NMF
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
# 데이터 불러오기
iris = load_iris()
iris_data = iris.data
# NMF클래스를 이용하여 사용해보기. 2개의 컴포넌트
nmf = NMF(n_components=2)
# 학습
iris_nmf = nmf.fit_transform(iris_data)
# 시각화
plt.scatter(x=iris_nmf[:,0], y=iris_nmf[:,1], c=iris.target)
plt.xlabel('NMF Component 1')
plt.ylabel('NMF Component 2')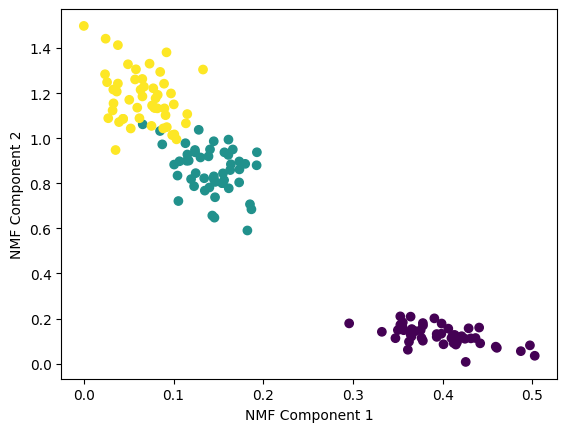
군집화
분류 vs 군집화
분류(Classification)
- 범주의 수 및 각 개체의 범주 정보를 '사전에 알 수 있으며', 입력 변수 값으로부터 범주 정보를 유추하여 새로운 개체에 대해 가장 적합한 범주로 할당하는 문제
- 지도학습
군집화(Clustering)
- 군집의 수, 속성등이 '사전에 알려져있지 않으며' 최적의 구분을 찾아가는 문제
- 비지도 학습
군집분석(Clustering) 이란?
각 개체의 동질성을 측정하여 동질성이 높은 '대상 군집'을 탐색하고, 군집에 속한 개체들의 동질성과 서로 다른 군집에 속한 개체간의 이질성을 규명하는 통계 분석 방법
K-평균 알고리즘 이해
K-평균은 군집화에서 가장 일반적으로 사용되는 알고리즘이다. 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택하는 군집화 기법이다.
수행과정
-
K 값을 초기값으로 먼저 받고, K개의 초기 군집의 임의 중심점을 설정한다
-
각 개체와 군집 중심점 사이의 거리를 계산한다.
-
가장 가까운 중심점 군집으로 재할당한다
-
변경된 군집을 기준으로 개체와 군집 중심점 사이의 거리를 다시 계산
-
3~4 단계를 군집의 변동이 없을 때까지 반복한다.
↓
-
군집 중심점(centroid)라는 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택
-
군집 중심점은 선택된 포인트의 평균 지점으로 이동하고 이동된 중심점에서 다시 가까운 포인트를 선택한다
-
이 과정을 반복하다가 더이상 중심점의 이동이 없으면 반복을 멈추고 해당 중심점에 속하는 포인트들을 군집화 한다.
장점
- 알고리즘이 쉽고 간결하다(계산 시간 짧음)
- 비지도학습이기 때문에 사전 라벨 데이터가 필요없다
- 데이터 변환 없이 그 자체로 이용할 수 있어 데이터 구조가 간단하다
단점
- 거리 기반의 알고리즘이므로 속성(피처)의 개수가 많으면 군집화 정확도가 떨어진다
- 반복 횟수가 많아지면 수행 시간이 매우 느려진다.
- 초기 군집 수(K)에 따라 결과가 달라지는데, 몇 개의 군집을 선택해야 할지 가이드 하기가 어렵다. (K 설정에 대한 가이드가 어렵다)
- 범주형 변수 사용이 불가하다
KMeans 클래스(사이킷 런)
KMeans 클래스는 아래와 같은 초기화 파라미터를 가지고 있다.
KMean(n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001,
precompute_distances='auto', verbose=0, random_state=None,
copy_x=True, n_jobs=1, algorithm='auto')n_clusters : 초기 파라미터 중 가장 중요한 파라미터. 군집화할 개수 = 군집 중심점의 개수를 의미한다
init : 초기에 군집 중심점의 좌표를 설정할 방식을 말한다. 보통은 임의로 중심을 설정하지 않고 'k-means++' 방식으로 최초 설정한다
max_iter : 최대 반복 횟수. 이 횟수 이전에도 모든 데이터의 중심점 이동이 없으면 종료한다.
군집화와 관련된 주요 속성은 아래와 같다.
labels_ : 각 데이터 포인트가 속한 군집 중심점 레이블
cluster_centers_ : 각 군집 중심점 좌표(Shape는 [군집 개수, 피처 개수]). 이를 이용하면 군집 중심점 좌표가 어디인지 시각화할 수 있다.
붓꽃 데이터로 K-평균 세트 군집화
sklearn.cluster의 KMeans()로 K-Means를 수행할 수 있다.
from sklearn.preprocessing import scale
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# 데이터 불러오기 및 DataFrame으로 변환(+컬럼명 변환
iris = load_iris()
X_feature = iris.data
y_label = iris.target
# target 변수를 제외하고 데이터 프레임으로 생성
iris_df = pd.DataFrame(data=X_feature, columns=['sepal_length', 'sepal_width', 'petal_length', 'petal_width'])
iris_df[:3]
붓꽃 데이터 세트를 3개의 그룹으로 군집화해보자. k-means는 데이터를 나누는(train_test_split) 과정이 필요하지 않다. 바로 KMeans 사용해보자
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=0)
# 책에서는 kmeans.fit(iris_df)
kmeans.fit(X_feature)
fit() 수행시 iris_df 데이터에 대한 군집화 수행 결과가 kmeans 객체 변수로 반환되었을 것이다. 속성값을 출력해보면 데이터가 어떤 중심에 속해있는지 알 수 있다고 함
print(pd.Series(kmeans.labels_).value_counts())2 61
0 50
1 39
dtype: int64n_clusters 값을 3으로 주었으니, 값이 0, 1, 2,로 분류된 모습을 확인할 수 있었다.
kmeans.labels_array([1, 0, 0, 1, 0, 1, 2, 2, 0, 1, 0, 1, 0, 0, 0, 1, 2, 2, 0, 1, 1, 2,
0, 0, 1, 0, 2, 1, 1, 1, 0, 0, 1, 0, 2, 2, 0, 2, 2, 1, 2, 1, 1, 1,
0, 0, 0, 1, 0, 0, 0, 2, 1, 1, 1, 1, 2, 2, 0, 0, 1, 1, 0, 2, 2, 1,
2, 2, 1, 2, 2, 0, 0, 1, 0, 1, 2, 2, 2, 1, 1, 0, 0, 2, 2, 0, 0, 1,
0, 2, 1, 1, 2, 0, 2, 0, 0, 1, 1, 2, 2, 0, 1, 0, 1, 0, 2, 0, 1, 2,
0, 1, 2, 1, 0, 0, 0, 2, 1, 1, 2, 2, 1, 0, 2, 0, 1, 2, 1, 0, 1, 2,
2, 2, 0, 2, 2, 0, 2, 1, 1, 1, 0, 2, 2, 0, 1, 1, 2, 0, 2, 1, 1, 1,
0, 2, 2, 2, 0, 0, 2, 1, 1, 1, 0, 0, 2, 1, 2, 2, 0, 2, 0, 2, 1, 1,
0, 1, 0, 2, 0, 1, 2, 2, 2, 0, 1, 2, 0, 0, 1, 1, 2, 2, 2, 2, 1, 2,
0, 2])labels_ 속성은 각 데이터 포인트가 속한 군집 중심점 레이블이다.
iris_df['target'] = iris.target
iris_df['cluster'] = kmeans.labels_
iris_result = iris_df.groupby(['target','cluster']).size()
iris_resulttarget cluster
0 1 50
1 0 48
2 2
2 0 14
2 36
dtype: int64- target이 0인 데이터는 모두 1번 군집으로 잘 분류
- target이 1인 데이터는 2개만 0번 군집으로, 나머지는 2번 군집으로 분류
- target이 2인 데이터는 36개가 0번 군집으로, 14개가 2번 군집으로 분류
군집화 알고리즘 테스트를 위한 데이터 생성
사이킷런 패키지에는 다양한 유형의 군집화 알고리즘을 테스트해보기 위한 간단한 데이터 생성기를 제공한다. 대표적인 군집화용 데이터 생성기로는 make_blobs()와 make_classification() API가 있다.
make_blobs(): 대표적인 군집화 데이터 생성기로 개별 군집의 중심점과 표준 편차 제어 기능이 있다.make_classfication(): 역시 대표적인 군집화 데이터 생성기로 노이즈를 추가할 수 있다.
make_blobs()를 이용해 가상데이터를 생성한다.
from sklearn.datasets import make_blobs
# make_blobs 로 데이터 생성
X, y = make_blobs(n_samples=200, n_features=2, centers=3, cluster_std=0.8, random_state=0)
print(X.shape, y.shape)
# target 값 분포
unique, counts = np.unique(y, return_counts=True)
print(unique, counts)(200, 2) (200,)
[0 1 2] [67 67 66]centers는 군집의 개수인데, 만약 ndarray 형태로 입력하면 개별 군집 중심점의 좌표로 인식하게 된다. cluster_std는 생성될 군집 데이터의 표준편차를 의미하며 각 군집별로 설정이 가능.
좀 더 데이터 가공을 편리하게 하기 위해서 위 데이터 세트를 DataFrame화 후 시각화 해보자
# 데이터 프레임 생성
cluster_df = pd.DataFrame(X, columns=["ftr1","ftr2"])
cluster_df["target"] = y
# target 값 종류
target_list = np.unique(y)
# 가상 데이터 시각화
markers=['o', 's', '^']
for target in target_list:
target_cluster = cluster_df[cluster_df['target'] == target]
plt.scatter(x=target_cluster['ftr1'], y=target_cluster['ftr2'],
edgecolor='k', marker=markers[target] )
plt.show()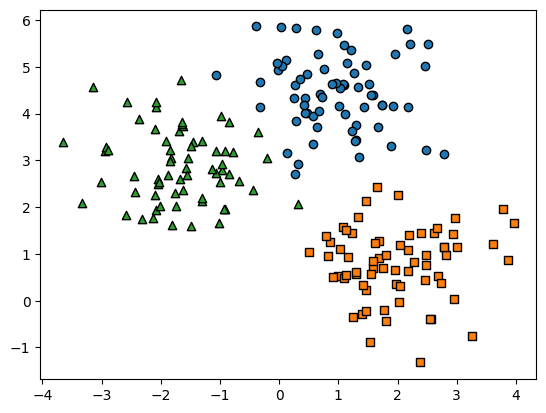
이렇게 만들어진 데이터 세트에 KMeans 군집화를 수행한 뒤에 군집별로 시각화해 보자.
# K-Means 객체 생성
kmeans = KMeans(n_clusters=3, init="k-means++", max_iter=200, random_state=0)
# cluster label (fit 후 labels_, fit_predict의 결과가 같았다.)
cluster_labels = kmeans.fit_predict(cluster_df.iloc[:,:-1])
cluster_df["kmeans_label"] = cluster_labels
# 개별 클러스터의 중심 위치 좌표
centers = kmeans.cluster_centers_K-Means를 수행하고 데이터 프레임에 cluster label을 추가, 이후 clustercenters 속성의 각 군집 중심점 좌표를 시각화를 위해 추출하였다.
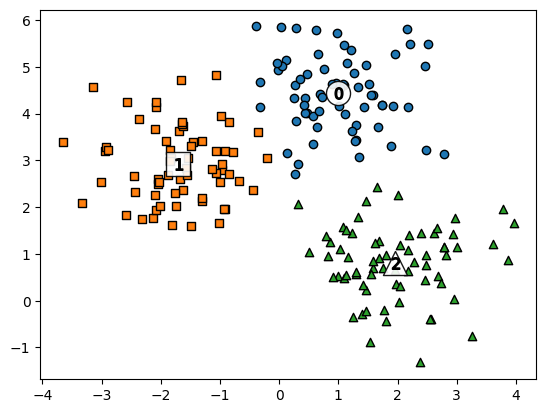
각 군집과 군집별 중심위치를 시각화하였다. 음 제법 잘 매핑 된것으로 보인다...
cluster_df.groupby(['target','kmeans_label']).size()target kmeans_label
0 0 66
1 1
1 2 67
2 1 65
2 1
dtype: int64실제로 target 0,2에서 각각 1건씩만 다르게 분류되고 나머지는 잘 매핑된 모습!