[제어공학] Bode Plot과 Margin

지금까지 저희는 time response method로 제어 모델들을 해석하였습니다.
이번에는 frequncy response method로 한번 해석해보겠습니다.

Gain

제어공학을 다루며 gain이라는 말을 많이 들었고, 들을 것입니다.
Gain이란 다음을 말합니다.

추가적으로 DC gain이란, 주파수$(\omega)$가 $0$일 때의 gain을 뜻합니다.

Margin

margin이란 여유를 뜻하는 단어입니다. 제어공학에서의 margin은 gin margin과 phase margin 두 가지가 있습니다.

Gain Margin

Gain Margin($G.M.$)은 클 수록 시스템이 안정하고 제어 대상의 prameter 변화에 대한 강인성이 커지는 지표입니다.
Gain margin의 정의는 다음과 같습니다.

$Phase$가 $-180\degree$일 때, $Magnitude(gain)$가 $1(0db)$인 곳으로부터 떨어진 정도를 나타냅니다.

따라서 $K$값을 G.M.만큼 배율을 키워도 시스템이 안정하다는 것을 의미합니다.

Phase Margin

P.M. 역시 클 수록 시스템이 안정하다는 것을 나타내는 지표입니다.

$Magnitude(gain)$이 1배(0db)이 될 때, $Phase$가 $-180\degree$ 보다 작은 정도를 Phase Margin이라고 합니다.

따라서 $P.M.[rad] \over \omega_{gc}[rad/s]$만큼의 time delay가 추가 되더라도 시스템이 안정하다는 것을 의미합니다.

만약 $P.M.<60\degree$이라면 $\zeta=\frac{P.M.}{100}[deg]$로 근사할 수 있습니다.

BandWidth

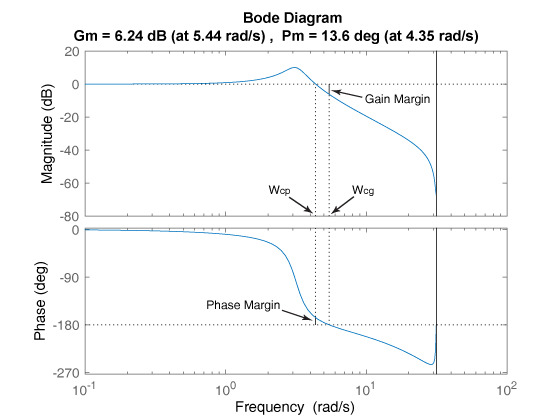
앞에서 배운 내용을 바탕으로 Gain Margin을 보면 Phase가 $-180\degree$가 되는 부분에서 쭈욱 위로 올라가서 Magnitude가 0과의 여유가 얼마나 되는지가 표시되어 있는 것을 볼 수 있습니다.
Phase Margin의 경우 약간 반대로, Magnitude가 0인 부분에서 쭈욱 아래로 내려와 Phase가 $-180\degree$가 되는 부분까지 얼마나 여유가 되어 있는지 표시되어 있습니다.

위의 보드 선도를 보면, $\omega$가 $1$까지는 거의 gain이 0이라고 볼 수 있습니다.
하지만 그 이후 급격히 Phase가 떨어지게 됩니다.
Phase가 $-180\degree$가 되면 입력과 출력의 상이 정반대이므로 대부분 발산하게 됩니다.
따라서 Phase가 $-180\degree$에 가까워질수록 뒤쳐지므로 성능이 점점 감소하게 됩니다. 실제 성능 감소는 Magnitude를 보면 알 수 있습니다.

BandWidth란 성능(Magnitude)이 $0db=1$배 에서 $-3dB=0.707$배까지 감소하게 되는 주파수까지의 범위를 뜻합니다.

즉, 명령에 대한 출력의 추종성능을 의미합니다.

만약 open loop이고 $-225\degree < Phase < -135\degree$ 이라면, $-6dB$ 시점까지로 BandWidth를 근사할 수 있습니다.

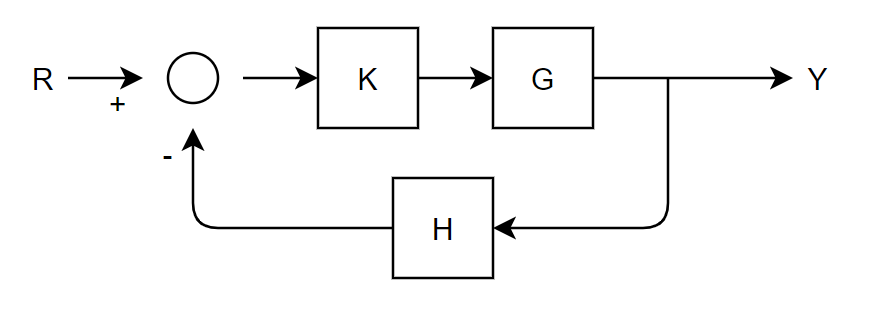
위의 블럭선도를 closed loop transfer function으로 나타내면 다음과 같습니다.

open loop transfer function은 다음과 같이 나타낼 수 있습니다.

Matlab Example

margin을 확인할 수 있는 코드입니다.
Phase가 $-180\degree$로 무한히 수렴하고 있고, Magnitude는 음의 무한대로 발산하고 있기 때문에 Gain margin은 $\infin$입니다.

s = tf('s');
G = 1/(s^2+0.5*s+1);
margin(G)

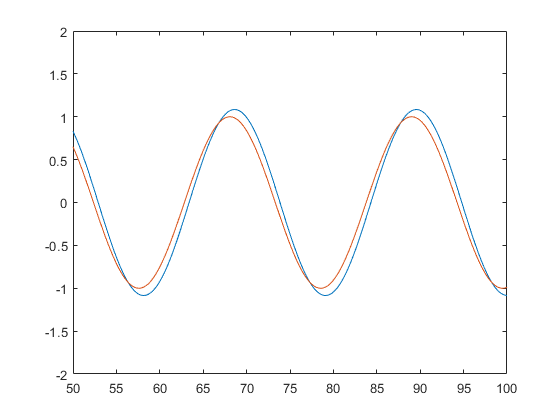
출력이 응답에 비해 약 $1\over10$정도 낮은 모습을 보여주고 있습니다.

G = 1/(s^2+0.5*s+1);
w = 0.3;
t = 0:0.1:100;
u = sin(w*t);
[y, t] = lsim(G, u, t);
plot(t, y, t, u)