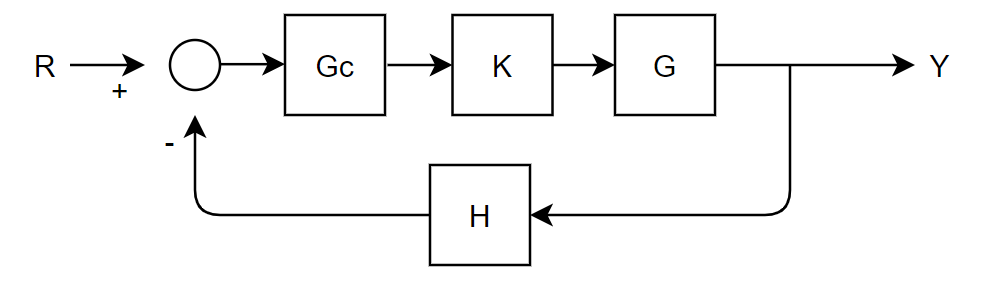
Compensator
제어기를 설계할 때는 우선적으로 K p K_p K p e s s e_{ss} e s s K p K_p K p K i K_i K i P . M . P.M. P . M . G c G_c G c P . M . P.M. P . M .
G c G_c G c K G C G H KG_CGH K G C G H ∠ K + ∠ G c + ∠ G + ∠ H \angle K +\angle G_c +\angle G +\angle H ∠ K + ∠ G c + ∠ G + ∠ H
보상기는 다음과 같이 설계됩니다.
G c ( s ) = K ( s + z ) s + p = 1 + α τ s 1 + τ s G_c(s)=\frac{K(s+z)}{s+p}=\frac{1+\alpha\tau s}{1+\tau s} G c ( s ) = s + p K ( s + z ) = 1 + τ s 1 + α τ s Phase Lead Compensator (진상보상기)
특정 주파수에서 Phase를 끌어올림으로써 P . M . P.M. P . M .
B.W.가 증가하기 때문에 B.W.를 좀 더 키울 필요가 있다면 Phase lead compensator 를 사용하는 것이 좋습니다.
설계
K p K_p K p K i K_i K i e s s e_{ss} e s s steady state error 조건을 만족시킵니다.원하는 댐핑계수를 얻기위한 P . M . P.M. P . M . Phase lead ϕ m \phi_m ϕ m i f P . M . < 60 ° , t h e n ζ = P . M . 100 [ d e g ] if\;\;P.M.<60\degree,\;\;then\;\;\zeta=\frac{P.M.}{100}[deg] i f P . M . < 6 0 ° , t h e n ζ = 1 0 0 P . M . [ d e g ]
sin ϕ m = α − 1 α + 1 \sin\phi_m=\frac{\alpha-1}{\alpha+1} sin ϕ m = α + 1 α − 1 α \alpha α 개루프 전달함수 K G ( j ω ) H ( j ω ) KG(j\omega)H(j\omega) K G ( j ω ) H ( j ω ) − 10 log α [ d B ] -10\log\alpha[dB] − 1 0 log α [ d B ] ω m \omega_m ω m
ω m = 1 / ( τ α ) \omega_m=1/(\tau\sqrt\alpha) ω m = 1 / ( τ α ) τ \tau τ K G c G H KG_cGH K G c G H bode plot 을 그리고 P . M . P.M. P . M .
보상기의 최종결과는 다음과 같습니다.
G c ( s ) = 1 + α τ s 1 + τ s G_c(s)=\frac{1+\alpha\tau s}{1+\tau s} G c ( s ) = 1 + τ s 1 + α τ s Example
T s ≤ 4 , ζ ≥ 0.45 T_s\leq4, \zeta \geq0.45 T s ≤ 4 , ζ ≥ 0 . 4 5
solve)
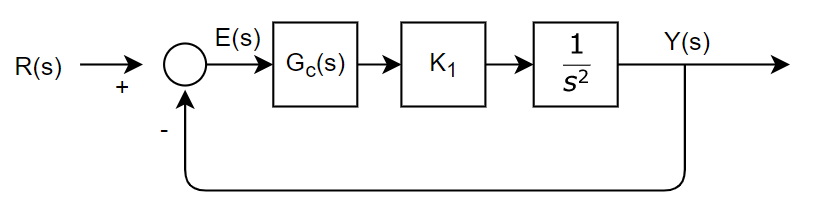
K 1 K_1 K 1
가장 먼저 ζ \zeta ζ ω n \omega_n ω n
T s = 4 ζ ω n ( 2 % c r i t e r i o n ) 4 ≥ 4 ζ ω n ω n ≥ 1 ζ = 1 0.45 = 2.22 ( ∵ m i n i m a l ζ ) T_s=\frac{4}{\zeta}{\omega_n}\;(2\%\;criterion)\\ 4\geq\frac{4}{\zeta\omega_n} \omega_n\geq\frac 1\zeta=\frac1{0.45}=2.22\;(\because minimal\; \zeta) T s = ζ 4 ω n ( 2 % c r i t e r i o n ) 4 ≥ ζ ω n 4 ω n ≥ ζ 1 = 0 . 4 5 1 = 2 . 2 2 ( ∵ m i n i m a l ζ ) Y R = K 1 s 2 1 + K 1 s 2 = K 1 s 2 + K 1 = ω n 2 s 2 + 2 ζ ω n s + ω n 2 ( ∵ 2 차 시스템의 s t a n d a r d f o r m ) → K 1 = ω n ≥ 2.22 → K 1 ≥ 4.93 \frac YR=\frac{\frac{K_1}{s^2}}{1+\frac{K_1}{s^2}}=\frac{K_1}{s^2+K_1}=\frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}(\because 2차\,시스템의\,standard\,form)\\ \rarr \sqrt{K_1}=\omega_n\geq2.22\\ \rarr K_1\geq4.93 R Y = 1 + s 2 K 1 s 2 K 1 = s 2 + K 1 K 1 = s 2 + 2 ζ ω n s + ω n 2 ω n 2 ( ∵ 2 차 시 스 템 의 s t a n d a r d f o r m ) → K 1 = ω n ≥ 2 . 2 2 → K 1 ≥ 4 . 9 3 안전계수를 고려하여 K 1 K_1 K 1
P . M . P.M. P . M .
openloop 전달함수는 K 1 G = K 1 s 2 = 10 ( j ω ) 2 = − 10 ω 2 K_1G=\frac{K_1}{s^2}=\frac{10}{(j\omega)^2}=-\frac{10}{\omega^2} K 1 G = s 2 K 1 = ( j ω ) 2 1 0 = − ω 2 1 0 Magnitude = 20 log 10 ∣ − 10 ω 2 ∣ 20\log_{10}|-\frac{10}{\omega^2}| 2 0 log 1 0 ∣ − ω 2 1 0 ∣
ω = 1 → 20 ω = 10 → 0 ω = 10 → − 20 \omega=1 \rarr 20\\ \omega=\sqrt{10} \rarr0\\ \omega=10 \rarr -20 ω = 1 → 2 0 ω = 1 0 → 0 ω = 1 0 → − 2 0 따라서 gain이 0이 되는 순간의 P . M . P.M. P . M . ω = 10 \omega=\sqrt{10} ω = 1 0
p h a s e = ∠ K 1 G = ∠ 10 s 2 = ∠ 10 ( j ω ) 2 = ∠ ( − 1 ) = − 180 ° phase=\angle K_1G=\angle \frac {10}{s^2}=\angle\frac{10}{(j\omega)^2}=\angle(-1)=-180\degree p h a s e = ∠ K 1 G = ∠ s 2 1 0 = ∠ ( j ω ) 2 1 0 = ∠ ( − 1 ) = − 1 8 0 ° 따라서 P . M . = 0 ° P.M.=0\degree P . M . = 0 ° P . M . P.M. P . M . Compensator 를 추가하여 P . M . P.M. P . M .
ζ = 0.45 \zeta=0.45 ζ = 0 . 4 5 P . M . ( ϕ m ) P.M.(\phi_m) P . M . ( ϕ m )
phase가 60 ° 60\degree 6 0 ° ζ = P . M . 100 \zeta=\frac{P.M.}{100} ζ = 1 0 0 P . M . ϕ m = 0.45 × 100 = 45 ° \phi_m=0.45\times100=45\degree ϕ m = 0 . 4 5 × 1 0 0 = 4 5 °
α \alpha α τ \tau τ ω m \omega_m ω m
sin ϕ m = α − 1 α + 1 → α = 5.828 − 10 log 10 α = − 7.655 d B \sin\phi_m=\frac{\alpha-1}{\alpha+1}\\ \rarr\alpha=5.828\\\,\\ -10\log_{10}\alpha=-7.655dB sin ϕ m = α + 1 α − 1 → α = 5 . 8 2 8 − 1 0 log 1 0 α = − 7 . 6 5 5 d B 따라서 보상시스템의 크기는 비보상시스템보다 7.655 d B 7.655dB 7 . 6 5 5 d B ω m \omega_m ω m
20 log 10 ∣ 10 s 2 ∣ = − 7.655 20 log 10 10 ω m 2 = − 7.655 ω m = 4.91 20\log_{10}|\frac{10}{s^2}|=-7.655\\\;\\ 20\log_{10}\frac{10}{\omega_m^2}=-7.655\\\;\\ \omega_m=4.91 2 0 log 1 0 ∣ s 2 1 0 ∣ = − 7 . 6 5 5 2 0 log 1 0 ω m 2 1 0 = − 7 . 6 5 5 ω m = 4 . 9 1 여기서 τ \tau τ ω m = 1 τ α \omega_m=\frac{1}{\tau\sqrt\alpha} ω m = τ α 1
ω m = 1 τ α τ = 1 ω m α = 1 4.91 5.828 = 0.0844 \omega_m=\frac 1{\tau\sqrt\alpha}\\\;\\ \tau=\frac{1}{\omega_m\sqrt\alpha}=\frac{1}{4.91\sqrt{5.828}}=0.0844 ω m = τ α 1 τ = ω m α 1 = 4 . 9 1 5 . 8 2 8 1 = 0 . 0 8 4 4
최종적으로 보상기 G c G_c G c
G c ( s ) = 1 + α τ s 1 + τ s = 1 + 0.49 s 1 + 0.0844 s ≈ 1 + s / 2 1 + s / 12 G_c(s)=\frac{1+\alpha\tau s}{1+\tau s}=\frac{1+0.49s}{1+0.0844s}\approx\frac{1+s/2}{1+s/12} G c ( s ) = 1 + τ s 1 + α τ s = 1 + 0 . 0 8 4 4 s 1 + 0 . 4 9 s ≈ 1 + s / 1 2 1 + s / 2
Phase leg Compensator (지상보상기)
Magnitude를 낮춤으로써 gain이 0이 되는 지점을 낮추어 P . M P.M P . M
B.W.가 감소하기 때문에 B.W.가 충분하다면 사용하는 Phase lead compensator를 사용하는것이 좋습니다.
설계
K p K_p K p K i K_i K i e s s e_{ss} e s s steady state error 조건을 만족시킵니다.원하는 댐핑계수를 얻기위한 P . M . P.M. P . M . Phase lead ϕ m \phi_m ϕ m i f P . M . < 60 ° , t h e n ζ = P . M . 100 [ d e g ] if\;\;P.M.<60\degree,\;\;then\;\;\zeta=\frac{P.M.}{100}[deg] i f P . M . < 6 0 ° , t h e n ζ = 1 0 0 P . M . [ d e g ]
ϕ m + 5 \phi_m+5 ϕ m + 5 ω c ′ \omega'_c ω c ′ ω c ′ \omega'_c ω c ′ G ( s ) H ( s ) G(s)H(s) G ( s ) H ( s ) ω c ′ \omega'_c ω c ′ P h a s e Phase P h a s e ω c ′ 10 \omega'_c\over10 1 0 ω c ′ τ = 10 / ω c ′ \tau=10/\omega'_c τ = 1 0 / ω c ′ 20 log 10 ∣ G ( j ω c ) H ( j ω c ) = 20 log 10 α 20\log_{10}|G(j\omega_c)H(j\omega_c)=20\log_{10}\alpha 2 0 log 1 0 ∣ G ( j ω c ) H ( j ω c ) = 2 0 log 1 0 α
보상기의 최종 결과는 다음과 같습니다.
G c ( s ) = 1 + τ s 1 + α τ s G_c(s)=\frac{1+\tau s}{1+\alpha\tau s} G c ( s ) = 1 + α τ s 1 + τ s Example
e s s ≤ 1 40 , ζ ≥ 0.45 e_{ss}\leq\frac1{40}, \zeta \geq0.45 e s s ≤ 4 0 1 , ζ ≥ 0 . 4 5
solve)
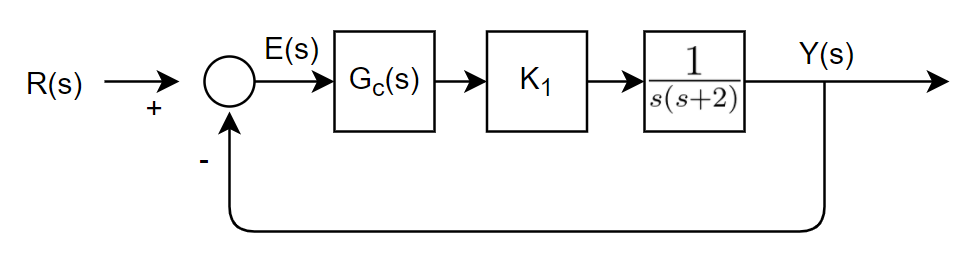
G c ( s ) G_c(s) G c ( s ) K K K
c o n d i t i o n : e s s ≤ 1 40 E ( s ) = R ( s ) − Y ( s ) = 1 1 + K 1 G e s s ≤ lim s → 0 s ⋅ E ( s ) = lim s → 0 s ⋅ 1 1 + K 1 s ( s + 2 ) R ( s ) = lim s → 0 s ⋅ s 2 + 2 s s 2 + 2 s + K 1 ⋅ 1 s 2 = 1 K 1 ≤ 1 40 K 1 ≥ 40 condition:\;e_{ss}\leq \frac1{40}\\\;\\ E(s)=R(s)-Y(s)=\frac{1}{1+K_1G}\\\;\\ \begin{aligned} e_{ss}\leq\displaystyle\lim_{s\rarr0}s\cdot E(s)&=\displaystyle\lim_{s\rarr0}s\cdot\frac{1}{1+\frac{K_1}{s(s+2)}}R(s)\\ &=\displaystyle\lim_{s\rarr0}s\cdot\frac{s^2+2s}{s^2+2s+K_1}\cdot\frac1{s^2}\\ &=\frac{1}{K_1}\leq\frac{1}{40}\end{aligned}\\ K_1\geq40 c o n d i t i o n : e s s ≤ 4 0 1 E ( s ) = R ( s ) − Y ( s ) = 1 + K 1 G 1 e s s ≤ s → 0 lim s ⋅ E ( s ) = s → 0 lim s ⋅ 1 + s ( s + 2 ) K 1 1 R ( s ) = s → 0 lim s ⋅ s 2 + 2 s + K 1 s 2 + 2 s ⋅ s 2 1 = K 1 1 ≤ 4 0 1 K 1 ≥ 4 0 K 1 K_1 K 1 40 40 4 0
P . M . P.M. P . M .
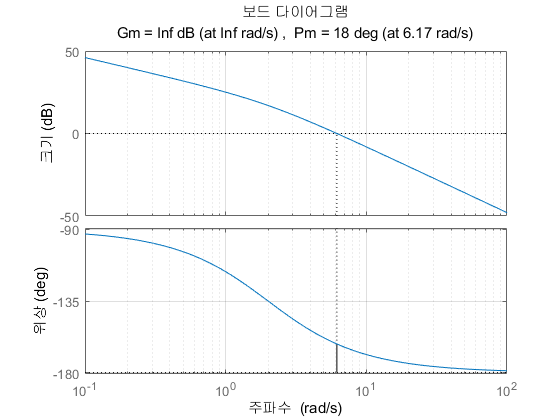
40 j ω ( j ω + 2 ) \frac{40}{j\omega(j\omega+2)} j ω ( j ω + 2 ) 4 0 P . M . P.M. P . M . 18 ° 18\degree 1 8 ° phase 가 60 ° 60\degree 6 0 ° ζ = P . M . 100 \zeta=\frac{P.M.}{100} ζ = 1 0 0 P . M . ϕ m = 0.45 × 100 = 45 ° \phi_m=0.45\times100=45\degree ϕ m = 0 . 4 5 × 1 0 0 = 4 5 °
P . M . = 100 × 0.45 = 45 ° P.M.=100\times0.45=45\degree P . M . = 1 0 0 × 0 . 4 5 = 4 5 ° 필요한 P . M . P.M. P . M . 45 + 5 = 50 ° 45+5=50\degree 4 5 + 5 = 5 0 ° ω c ′ \omega_c' ω c ′ 1.5 r a d / s e c 1.5rad/sec 1 . 5 r a d / s e c
τ \tau τ
τ = 10 ω c ′ = 6.67 \tau=\frac{10}{\omega_c'}=6.67 τ = ω c ′ 1 0 = 6 . 6 7
α \alpha α
ω c ′ = 1.5 \omega_c'=1.5 ω c ′ = 1 . 5 40 j ω ( j ω + 2 ) \frac{40}{j\omega(j\omega+2)} j ω ( j ω + 2 ) 4 0 Gain 은 다음 식을 이용하여 구할 수 있습니다.
α = ∣ 40 j ω c ( j ω c + 2 ) ∣ = 10.67 \alpha=\left\lvert\frac{40}{j\omega_c(j\omega_c+2)}\right\rvert=10.67 α = ∣ ∣ ∣ ∣ ∣ j ω c ( j ω c + 2 ) 4 0 ∣ ∣ ∣ ∣ ∣ = 1 0 . 6 7
최종적으로 보상기 G c G_c G c
G c ( s ) = 1 + τ s 1 + α τ s = 1 + 6.67 s 1 + 71.17 s G_c(s)=\frac{1+\tau s}{1+\alpha\tau s}=\frac{1+6.67s}{1+71.17s} G c ( s ) = 1 + α τ s 1 + τ s = 1 + 7 1 . 1 7 s 1 + 6 . 6 7 s