[제어공학] Root Locus

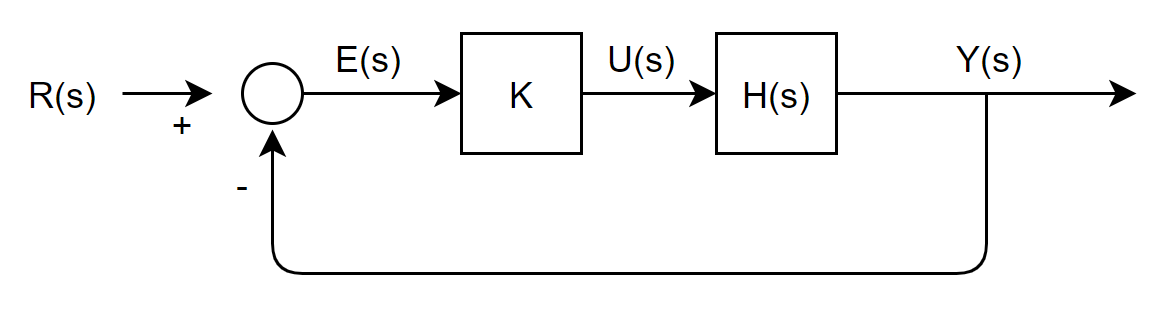
위와 같은 블럭선도가 있다고 합니다.
위의 블럭선도의 전달함수를 구하면 다음과 같습니다.

이 전달함수의 $pole$은 분모가 0이 되는 해 $s$입니다.
$H=\frac{b(s)}{a(s)}$이라고 하면, 다음과 같이 정리할 수 있습니다.

최종적으로 $\frac YR$의 $pole$은 $1+kH=0$이 결정하게 됩니다.

$\therefore$ 우리는 $k$를 변화시킴으로써 다른 $pole$을 얻을 수 있습니다.

Root Locus method

$k$를 변화시키며 $Y\over R$의 $pole$을 같은 복소평면에 그리고, 적절한 출력 반응이 예상되는 $pole$의 위치를 선정하는 방법의 하나입니다.

$k$가 $pole$을 변화시킬 수 있다는 사실을 알았으니 극단적인 두 가지 경우를 예상해봅니다.

1. $k=0\;\;\;→ a(s)=0$의 근$(H(s)의\;pole)$이 $Y\over R$의 $pole$이 됩니다.
2. $k=\infin \;\,→ 0+b(s)=0$의 근$(H(s)의 zero$가 $Y\over R$의 $pole$이 됩니다.

Matlab example

아래 전달함수는 $pole$의 개수가 $zero$의 개수보다 적습니다.
이러한 경우에는 부족한 $pole-zero$의 개수만큼 복소평면상의 $\infin$ 위치의 $zero$로 발산하게 됩니다.

num = [1, 7];
% 두 n차 방정식의 곱을 구할 수 있다.
den = conv(conv([1, 0], [1, 5]), conv([1, 15], [1, 20]));
% root locus를 그려준다.
rlocus(num, den)
axis([-22, 3, -15, 15])

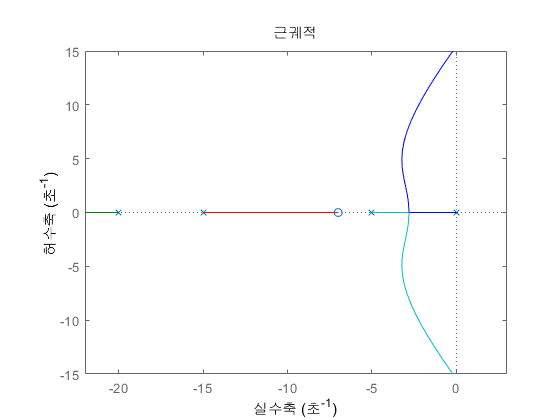
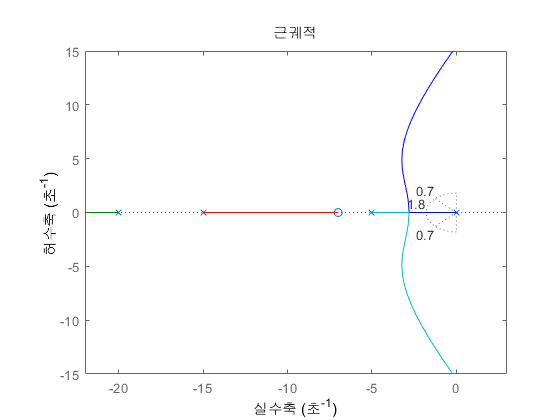
2개의 오른쪽 $pole$이 위/아래로 발산하는 모습을 볼 수 있습니다.

zeta = 0.7;
Wn = 1.8;
% Wn이 같을 때의 궤적, zeta가 같을 때의 궤적을 그려준다.
sgrid(zeta, Wn)