Final Value Theorem

final value theorem이란 left half plane에 pole이 모여 있다면 다음과 같은 공식이 성립한다는 의미입니다.

PID Control

고전제어 이론의 대표적인 제어법은 PID 제어입니다. 실제 산업에서 많이 적용하고 있는 제어법으로 PID 제어기의 전달함수는 비례, 미분, 적분기 3개의 항으로 이루어져 있습니다.
$K_p, K_I, K_D$를 각각 비례, 미분, 적분 gain이라고 합니다.

• 전달함수
  $G(s)=K_p+\frac{K_I}{s}+K_Ds$
• 시간영역에서 출력방정식
  $y(t)=K_p\cdot e(t)+K_I\cdot \int_0^te(\tau)d\tau+K_D \frac{d}{dt}e(t)$

1. $K_p$가 커지면 출력의 변화 속도가 빨라집니다.
   • 목표값에 도달하여도 적분값이 양수로 유지되므로 $PO$가 커집니다.
2. $K_I$가 커지면 $PO$가 커지고 $t_s$가 빨라집니다.
   • 제어가 불안정하지만 $K_I$값이 $0$이 아니면 무조건 $e_{ss}=0$으로 수렴합니다.
3. $K_D$가 커지면 $PO$가 작아지고 수렴이 느리지만 안정적입니다.
   • $K_D$가 커질수록 동특성 개선 효과가 있습니다.
   • error에 노이즈가 존재하면 $\frac{de}{dt}$가 매우 커지므로 출력이 oscillate 하게 됩니다.

response	$t_r$	$PO$	$t_s$	$e_{ss}$
$K_p$	↓	↑	↑	↓
$K_I$	↓	↓	↓	0
$K_D$	↓	↓	↓	↓

---

PID gain Tuning

일반적인 PID 컨트롤러 디자인

1. $K_p$ gain을 올려 $t_r$을 향상시킵니다.
2. $K_D$ gain을 올려 $M_p$를 최소화합니다.
3. $K_I$ gain을 올려 $e_{ss}$를 제거합니다.
4. 각 gain들을 조정하여 적절한 값을 찾습니다.

Zigler-Nichols tuning rule

일반적인 방법으로 적절한 gain값을 찾는 것은, 최선의 gain이라는 보장이 없고 시간이 오래 걸립니다.
지글러-니콜스 방법은 다음과 같이 $K_p$로 전체를 묶고 상수 $T$를 조절하여 적정값을 찾는 방법을 가집니다.

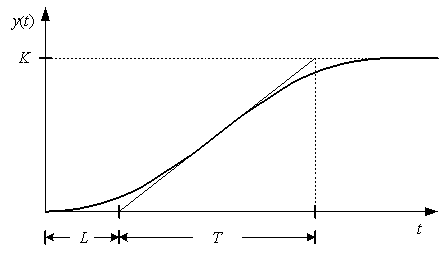
제 1방법: 과도응답법

플랜트의 단위계단응답이 다음과 같이 S자형으로 일정한 값에 수렴할 경우 사용할 수 있는 방법입니다.

제어기	$K_p$	$T_i$	$T_d$
P	$\frac{T}{L}$
PI	$0.9\frac{T}{L}$
PID	$1.2\frac RL$	$2L$	$0.5L$

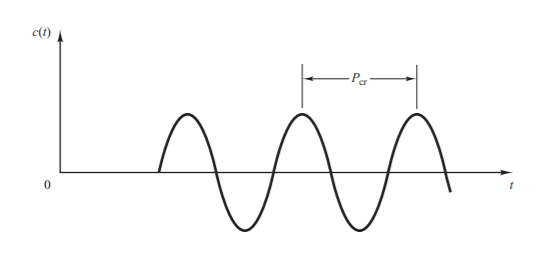
제 2방법: 한계감도법

제 1방법을 적용할 수 없는 경우, $P$제어 시스템을 구성한 후, $K_p$ gain을 증가시켜 임계상태(단진동하는 상태)를 만들고 이때의 gain($K_{cr}$)과 period($P_{cr}$)를 이용합니다.
과도응답법보다 우수한 성능을 보이지만, gain이 조금이라도 틀리면 발산할 위험이 있습니다.

제어기	$K_p$	$T_i$	$T_d$
P	$0.5K_{cr}$
PI	$0.45K_{cr}$	$\frac{P_{cr}}{1.2}$
PID	$0.6K_{cr}$	$0.5P_{cr}$	$0.125P_{cr}$

---

계전기 조정법

리밋사이클 진동을 유발하고 이로부터 dead time($\tau$)와 시정수 $T_p$를 구합니다.
한계감도법보다 안정한 영역에서 튜닝을 하기 때문에 좀 더 안전합니다.