
이번 강의에서는 Principal Component Analysis (PCA)에 대해 다룹니다. PCA는 데이터 차원 축소 기법으로, 데이터 분석과 시각화, 머신러닝 모델의 성능 향상에 매우 유용합니다. 특히, Part 1의 매트릭스 분해(Matrix Decomposition)와 Part 2의 볼록 최적화(Convex Optimization)와 연관지어 PCA의 수학적 원리를 설명합니다.
PCA의 동기
차원 축소의 필요성
고차원 데이터는 분석, 시각화, 모델링에 어려움을 줄 수 있습니다. 예를 들어, 2차원 데이터에서 두 번째 차원(X2)은 거의 0에 가깝고 의미가 없는 경우, 이를 무시하고 차원을 줄여 분석하는 것이 효율적입니다. PCA는 이러한 고차원 데이터를 저차원으로 축소하여 의미 있는 정보만을 남기고 분석하는 데 유용합니다.
예시
예를 들어, 집을 구매할 때 고려하는 다섯 가지 요소(집의 크기, 방의 개수, 화장실의 개수, 학교 근처 여부, 우범지역 여부)를 두 가지 요소(사이즈와 위치)로 축소하여 쉽게 결정할 수 있게 해줍니다.
PCA 알고리즘
- 센터링(Centering): 각 데이터에서 평균을 빼서 데이터의 중심을 원점으로 이동시킵니다.
- 스탠다드 데비에이션(Normalization): 각 차원의 분산이 1이 되도록 데이터를 정규화합니다.
- 데이터 공분산 행렬(Covariance Matrix): 공분산 행렬을 계산하고, 이 행렬의 고유값(Eigenvalue)과 고유벡터(Eigenvector)를 구합니다.
- 차원 축소(Target Dimension Reduction): 원하는 차원(M개)만큼 가장 큰 고유값에 해당하는 고유벡터를 선택하여 데이터를 축소합니다.
- 프로젝션(Projection): 선택된 고유벡터 공간으로 데이터를 투영하여 저차원 데이터를 얻습니다.
데이터 공분산 행렬
데이터 공분산 행렬 ( S )는 데이터 매트릭스 X 를 이용하여 다음과 같이 정의됩니다:

S = \frac{1}{n} X X^T
이 행렬은 항상 대칭(symmetric)이고 양의 정부호(positive definite)입니다. PCA는 이 공분산 행렬의 고유값과 고유벡터를 이용하여 차원을 축소합니다.
PCA의 수학적 원리
Variance Maximization
PCA의 목표는 데이터를 저차원 공간으로 투영했을 때 분산(variance)을 최대화하는 방향을 찾는 것입니다. 이를 위해 공분산 행렬의 고유값과 고유벡터를 사용합니다. 가장 큰 고유값에 해당하는 고유벡터가 가장 중요한 주성분(principal component) 방향이 됩니다.
증명 과정
- 기본 개념 정리: X는 원본 데이터, B는 투영 행렬, Z는 저차원 공간의 데이터입니다. Z의 분산을 최대화하는 방향을 찾는 것이 목표입니다.
- Optimization: 주어진 공분산 행렬 S에서 가장 큰 고유값과 이에 대응하는 고유벡터를 찾습니다.
- 수학적 증명: Lagrangian 함수와 KKT 조건을 이용하여 가장 큰 고유값과 고유벡터를 찾고, 이를 통해 최적의 투영 방향을 구합니다.
Low-Rank Approximation
PCA는 로우랭크 매트릭스 근사(low-rank matrix approximation)와 밀접한 관련이 있습니다. 에카르트-영 정리에 따르면, PCA는 주어진 데이터 매트릭스를 저차원 공간에서 가장 잘 근사하는 방법을 제공합니다.
효율적인 PCA 계산
데이터 차원이 데이터 개수보다 큰 경우, 공분산 행렬의 고유값 분해 대신 SVD(Singular Value Decomposition)를 사용하여 효율적으로 PCA를 계산할 수 있습니다. SVD는 다음과 같이 표현됩니다:
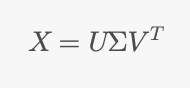
X = U \Sigma V^T
여기서 U와 V는 각각 좌우 고유벡터, \Sigma는 고유값 행렬입니다. 이를 이용하여 공분산 행렬의 고유값과 고유벡터를 효율적으로 구할 수 있습니다.
결론
PCA는 고차원 데이터를 저차원으로 축소하여 중요한 정보를 유지하면서 분석을 용이하게 합니다. 이를 통해 데이터의 시각화, 분석, 머신러닝 모델의 성능을 향상시킬 수 있습니다. 이번 강의에서는 PCA의 기본 개념, 알고리즘, 수학적 원리 및 효율적인 계산 방법을 다루었습니다.
다음 강의에서는 PCA의 응용과 더 발전된 차원 축소 기법에 대해 다룰 예정입니다.
이 요약본은 LG Aimers Academy의 교육 내용을 바탕으로 작성되었습니다.
