
이번 강의에서는 Convex Optimization(볼록 최적화)에 대해 다룹니다. Convex Optimization은 머신러닝 모델 학습에서 매우 중요한 주제로, 모델의 최적 파라미터를 찾는 과정과 밀접한 관련이 있습니다. 이 강의에서는 Convex Optimization의 기본 개념, KKT 조건, 라그랑주 함수 등을 설명하며, 이를 이해하는 데 필요한 핵심 내용을 다룹니다.
최적화 문제의 개요
머신러닝 모델을 학습할 때, 우리는 보통 특정 목적 함수를 최소화하는 최적화 문제를 해결하게 됩니다. 이러한 최적화 문제는 크게 두 가지로 나눌 수 있습니다:
- Unconstrained Optimization (무제약 최적화): 제약 조건이 없는 최적화 문제
- Constrained Optimization (제약 최적화): 특정 제약 조건을 만족하면서 최적화하는 문제
Convex Optimization은 제약 조건이 있는 최적화 문제의 한 유형으로, 목적 함수와 제약 조건이 모두 볼록 함수인 경우를 말합니다.
Gradient Descent
Gradient Descent는 최적화 문제를 해결하기 위한 기본적인 방법 중 하나입니다. 이 방법은 목적 함수의 기울기를 따라 내려가며 최소값을 찾는 방식입니다. 기본 알고리즘은 다음과 같습니다:
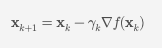
[ \mathbf{x}_{k+1} = \mathbf{x}_k - \gamma_k \nabla f(\mathbf{x}_k) ]
여기서 (\gamma_k)는 학습률(스텝 사이즈)이고, (\nabla f(\mathbf{x}_k))는 함수 (f)의 기울기입니다. Gradient Descent는 스텝 사이즈를 잘 조절하면 함수의 로컬 옵티마로 수렴하게 됩니다.
Stochastic Gradient Descent (SGD)
SGD는 데이터의 전체 배치 대신 무작위로 선택된 작은 배치로 Gradient Descent를 수행하는 방법입니다. 이는 계산 비용을 줄이고, 큰 데이터셋에서 효율적으로 동작합니다. Mini-batch Gradient Descent는 이와 유사한 방식으로, 작은 배치를 사용하여 업데이트를 수행합니다.
Momentum Gradient Descent
Momentum Gradient Descent는 이전 업데이트 방향을 고려하여 업데이트를 가속화하는 방법입니다. 기본 아이디어는 이전 단계의 기울기 방향을 현재 단계에서도 일정 부분 반영하는 것입니다. 이를 통해 수렴 속도를 높일 수 있습니다.
Constrained Optimization
제약 조건이 있는 최적화 문제를 해결하기 위해 라그랑주 함수를 사용합니다. 라그랑주 함수는 다음과 같이 정의됩니다:
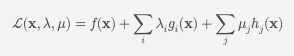
[ \mathcal{L}(\mathbf{x}, \lambda, \mu) = f(\mathbf{x}) + \sum{i} \lambda_i g_i(\mathbf{x}) + \sum{j} \mu_j h_j(\mathbf{x}) ]
여기서 (\lambda_i)와 (\mu_j)는 라그랑주 승수이며, 각각의 제약 조건 (g_i)와 (h_j)에 해당합니다. 이 함수는 원래의 최적화 문제를 변형하여 제약 조건을 포함한 형태로 만듭니다.
KKT 조건
KKT 조건은 제약 최적화 문제의 최적성을 확인하는 데 사용됩니다. 이 조건을 만족하면 해당 해가 최적 해임을 보장합니다. KKT 조건은 다음과 같습니다:

- Primal feasibility: (g_i(\mathbf{x}) \leq 0), (h_j(\mathbf{x}) = 0)
- Dual feasibility: (\lambda_i \geq 0)
- Stationarity: (\nabla f(\mathbf{x}) + \sum{i} \lambda_i \nabla g_i(\mathbf{x}) + \sum{j} \mu_j \nabla h_j(\mathbf{x}) = 0)
- Complementary slackness: (\lambda_i g_i(\mathbf{x}) = 0)
KKT 조건은 모든 제약 최적화 문제에 대해 필요 조건이며, Convex Optimization 문제에서는 충분 조건이기도 합니다.
Convex Optimization
Convex Set and Convex Function
Convex Optimization 문제는 볼록 집합(convex set)과 볼록 함수(convex function)에서 정의됩니다.
- Convex Set: 집합 내의 두 점을 잇는 선분이 항상 집합 내에 포함되는 경우
- Convex Function: 함수의 두 점을 잇는 선분의 함수값이 항상 함수의 그래프 위에 있는 경우
Convex Optimization Problem
볼록 최적화 문제는 다음과 같이 정의됩니다:

[ \min_{\mathbf{x}} f(\mathbf{x}) \quad \text{subject to} \quad \mathbf{x} \in \mathcal{C} ]
여기서 (f(\mathbf{x}))는 볼록 함수이고, (\mathcal{C})는 볼록 집합입니다.
Strong Duality
Strong Duality는 Convex Optimization 문제에서 프라이멀 문제와 듀얼 문제의 최적값이 같음을 의미합니다. 이를 통해 듀얼 문제를 풀어 프라이멀 문제의 최적값을 쉽게 찾을 수 있습니다.
결론
이번 강의에서는 Convex Optimization의 기본 개념과 이를 해결하기 위한 다양한 방법에 대해 정리하였습니다. Gradient Descent, Stochastic Gradient Descent, Momentum Gradient Descent 등 다양한 최적화 기법을 다루었고, 제약 조건이 있는 최적화 문제를 해결하기 위한 라그랑주 함수와 KKT 조건을 설명했습니다. Convex Optimization은 머신러닝 모델 학습에서 중요한 역할을 하며, 이를 이해하는 것이 좋은 모델을 만드는 데 큰 도움이 됩니다.
다음 강의에서는 Convex Optimization의 응용과 더 발전된 최적화 기법에 대해 다룰 예정입니다.
이 요약본은 LG Aimers Academy의 교육 내용을 바탕으로 작성되었습니다.
