[ML] 딥러닝의 깊이 있는 이해를 위한 머신러닝 1-2 (K-MOOC)

머신러닝의 수학적 기초

데이터

• 데이터를 $n \cdot \vec{x}$ 로 표현하며 아래 그림과 같습니다.
  

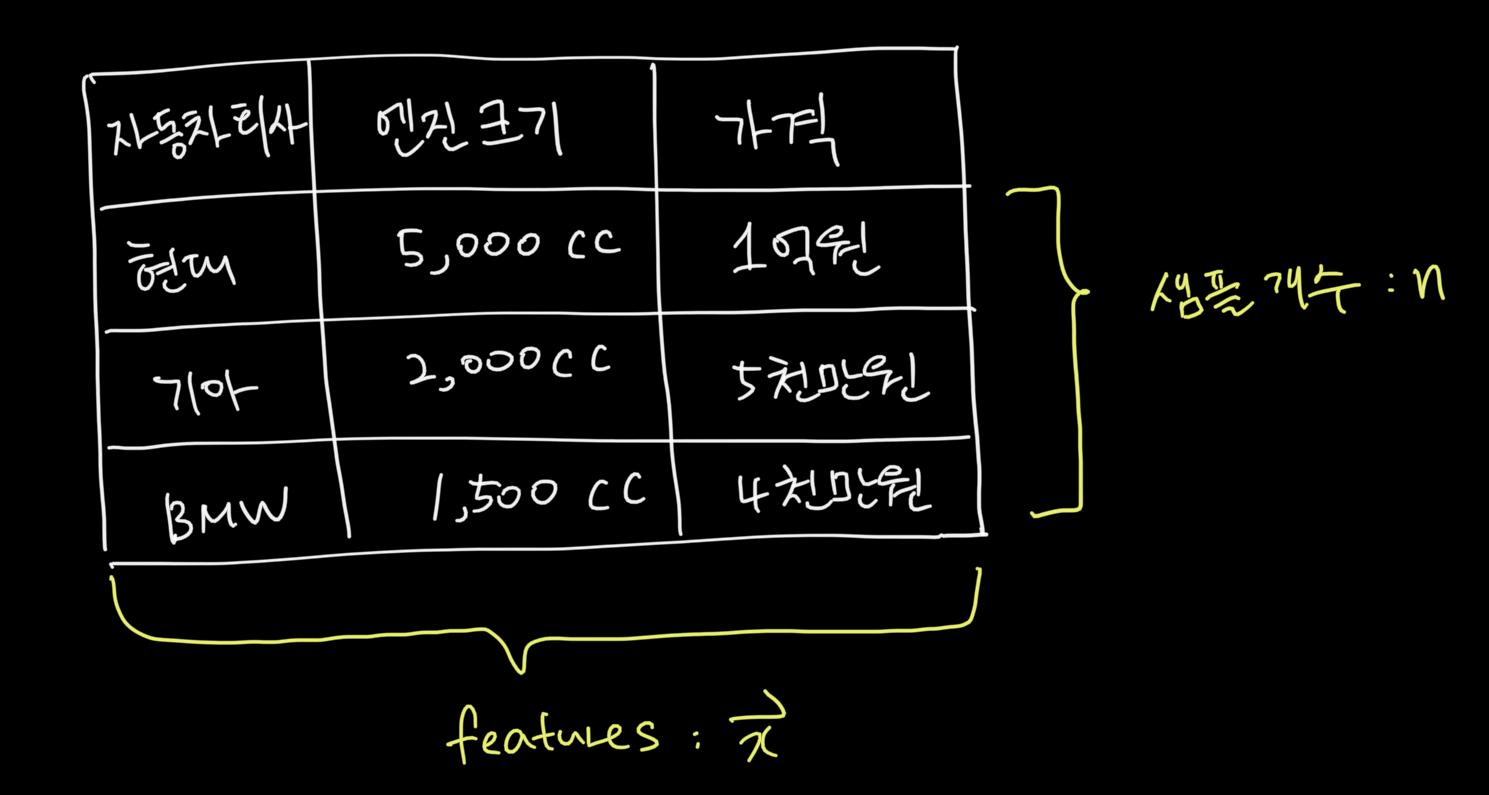
• label은 사용하고자 하는 사람이나 목적에 따라 다양합니다.

• label의 값은 데이터의 종류에 따라 다양합니다.

머신러닝의 기본 분류

Generative Model

해당 강의로는 Generative Model에 대한 이해가 부족하여 유튜브에서 허민석님의 설명을 참고하여 작성을 보완하였습니다.

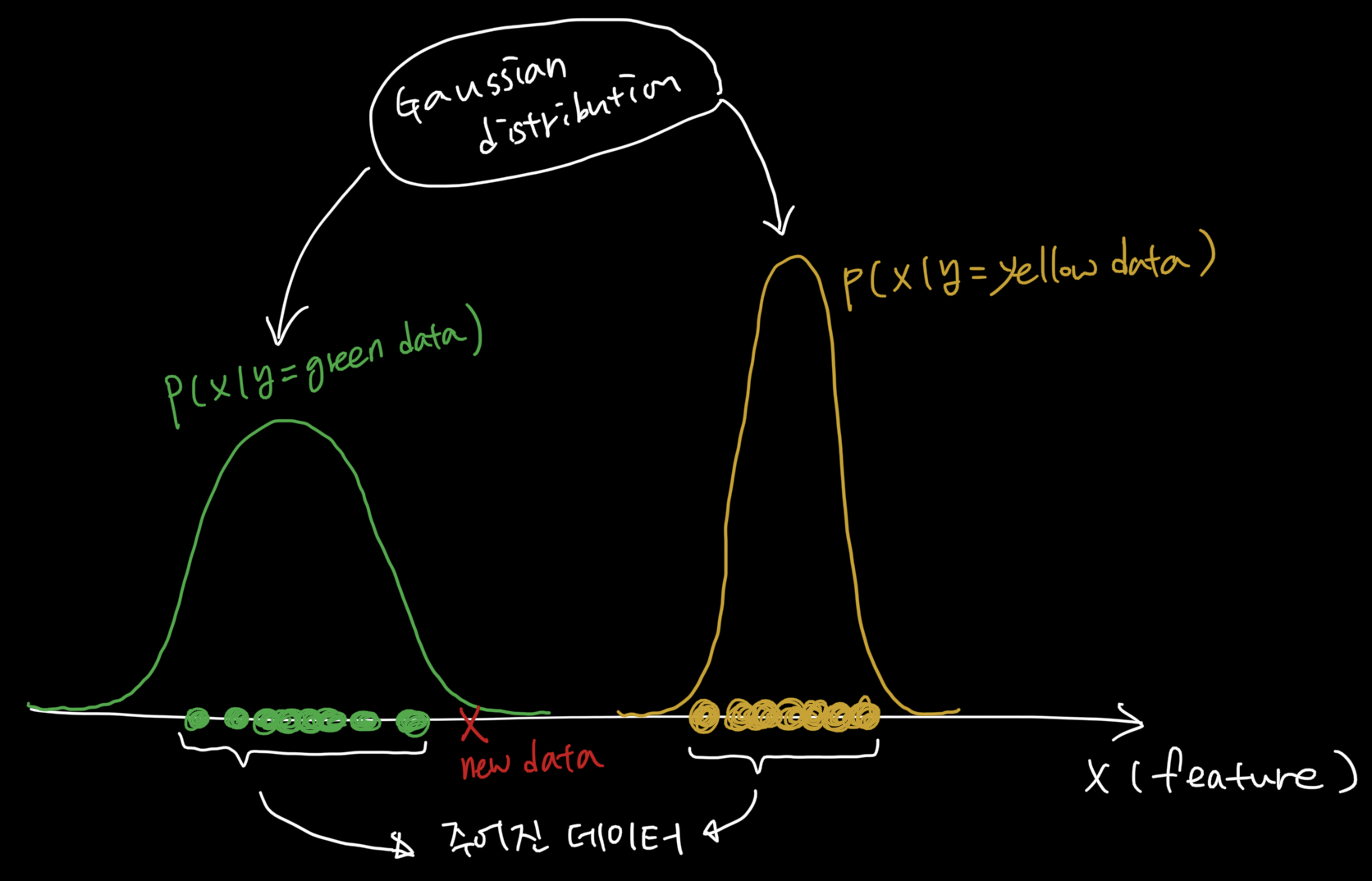
• 그림 설명 (해당 그림은 허민석님의 유튜브를 참고하여 작성했습니다.)

  • 현재 가지고 있는 데이터(초록색, 노란색 데이터)의 분포를 계산합니다. (위에서는 Gaussian Distribution을 사용했습니다.)

  • 새로운 데이터(new data)는 어느 분포에 속할까요?

  • 우리가 기존에 계산한 데이터의 확률 분포($p(x|y=green )$ and $p(x|y=yellow)$)를 이용하여 새로운 데이터가 어디에 속하는지 정합니다.

• 문제점 (단점)

  • 기존에 사용된 샘플들과의 거리 값을 기준으로 분류하므로 새로운 feature가 입력되면 결과값이 나오지 않습니다.

• 관점의 전환 (장점)

  • 새로운 샘플이 모르는 샘플이라는 결론을 내릴 때 장점이 됩니다.

• Generative Model의 분류

  • Parametric Model: 어떤 거리 값을 기반으로 값을 도출

  • Non-parametric Model: 거의 모든 샘플들을 활용하는 모델

Discriminative Model

Discriminative Model 은 학습에 존재하는 데이터들을 활용하여 decision boundary를 도출합니다.

• 단점

  • 새로운 샘플을 평가할 때 처음보는 샘플인지 알 수 없습니다.

• 장점

  • 완전히 다른 샘플이 들어오더라도 결론을 제시할 수 있습니다.

• Discriminative Model 중 선 하나 긋는 모델

  • Least Square

    • 모든 샘플들 간의 거리를 기반으로 가운데 선을 찾는 과정

    • 장점: 샘플들 간의 거리를 최소화 할 수 있는 선을 찾습니다.

    • 단점: 애초에 잘못된 샘플을 활용한 경우 도출한 결과(decision boundary)가 틀릴 수 있습니다.

  • Support Vector Machine

    • 가장 가까이 있는 샘플 2개를 집어서 그 두 개의 가운데를 가로지르는 decision boundary를 도출합니다.

Linear Model (선형 모델)

$y = f(\vec{w} \cdot \vec{x})=f(w_1x_1+w_2x_2+\dots+w_nx_n)$
($y$: label, $\vec{w}$: weights(구하고자 하는 값), $\vec{x}$: fetures)

• Linear regressor

  • 점수를 추정할 때 사용

  • Category 문제는 적용 불가능

• Linear Classifier

  • Category 문제에 적용 가능

Regularization & Nonlinearity

머신러닝의 효율성을 높이기 위해 활용합니다.

Regularization

• $\vec{w}$ 값 자체에 적용하게 되는 값

• 데이터에는 아무런 영향을 주지 않습니다.

• $\vec{w}$ 값에 대해 제한을 거는 존재가 Regularization

• 선형 모델이 노이즈에 대해 강인함을 갖도록합니다.

• L1-norm regularization & L2-norm regularization

  • 특정 feature의 크기가 너무 커지지 않도록 제어하는 역할을 수행합니다.

Nonlinearity

• 선 하나로 분류할 수 없는 상황

• Nonlinearity 문제를 Linear한 문제로 변형할 수 있습니다.