[ML] 딥러닝의 깊이 있는 이해를 위한 머신러닝 5-2 (K-MOOC)

Linear Regression Model

• $\vec{x} \cdot \vec{w} = y$

• 실제로 여러 학습 데이터에서 $\vec{w}$ 하나로는 라벨 예측 불가

Least Square

• 예측값과 실제값의 차이를 최소화 하는 선형 모델을 찾는 것

• $f(w) = \sum_{i=1}^{n}(wx_i-y_i)^2 \rarr$ Least Square Objective

• 위 그림기준으로 $f(w_{red}) < f(w_{green})$ 이다.

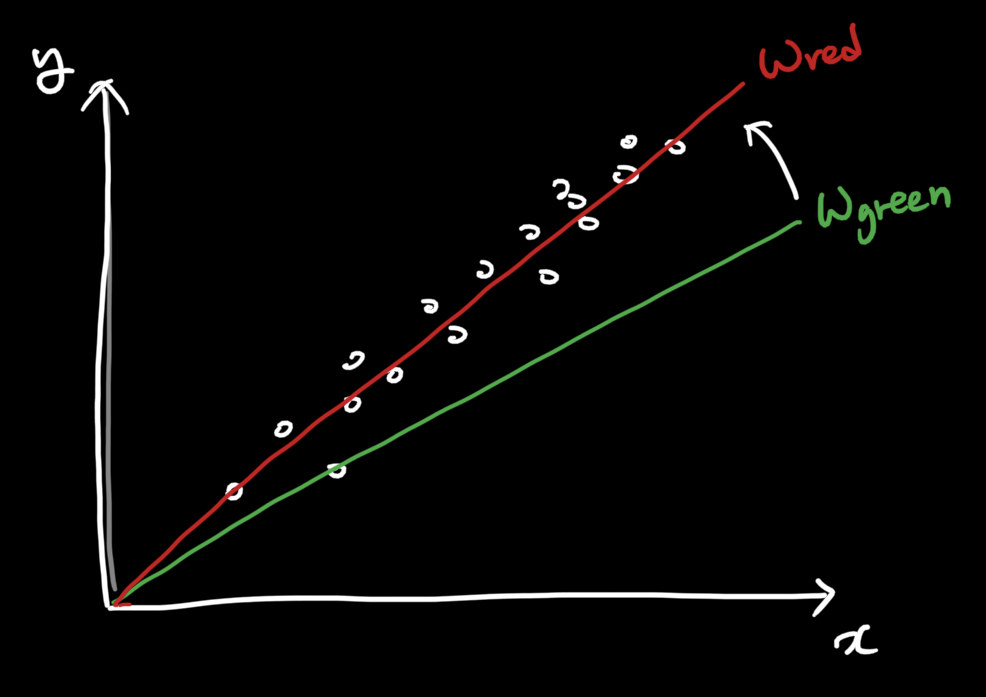
• $f(w) = \frac{1}{2} \sum_{i=1}^{n}(wx_i-y_i)^2$

• $f(w)$의 최소값을 찾는 문제이다. $w$에 관한 양의 이차 방정식 이므로 $f'(w)=0$ 인 $w$ 값을 찾으면 된다.

  • $f'(w) = \sum_{i=1}^{n}x_i(wx_i-y_i) = 0$

  • $\rarr w = \frac{\sum_{i=1}^nx_iy_i}{\sum_{i=1}^nx_i^2}$

N-dimension

• $f(\vec{w})=\frac{1}{2}\sum_{i=1}^{n}(\vec{w}^T \cdot \vec{x} - y_i)^2$

• $w$가 features 개수($d$)만큼 있으므로 총 $d$번 미분해야합니다.

• 미분 결과

  • $f(w_1, w_2, ..., w_d)=\frac{1}{2}(\sum_{j=1}^{d}w_jx_{ij})^2-(\sum_{j=1}^{d}w_jx_{ij})y_i+\frac{1}{2}y_i^2$

  • $\frac{\partial}{\partial w_k}f(w_1, w_2, ..., w_d) = (\sum_{j=1}^{d}w_jx_{ij})x_{ik} - y_ix_{ik} = (\vec{w}^T \vec{x} - y_i)x_{ik}$

• 벡터에서의 미분 동작 방법

  • $f(\vec{w}) = \vec{w}^T \vec{A} \vec{w} \rarr \nabla f(\vec{w}) = 2\vec{A} \vec{w}$ (단, $\vec{A}$ 가 symmetric 이어야합니다.)

• 벡터 형태의 Least Square

  • $f(\vec{w}) = \frac{1}{2}||\vec{x} \vec{w} - \vec{y}||^2 = \frac{1}{2}\vec{w}^T \vec{x}^T \vec{x} \vec{w} - \vec{w}^T \vec{x}^T \vec{y} + \frac{1}{2} \vec{y}^T \vec{y}$

  • $\nabla f(\vec{w}) = \vec{x}^T \vec{x} \vec{w} - \vec{x}^T \vec{y} = 0$

  • 위 식을 성립하는 $\vec{w}$가 $f(\vec{w})$ 최소일 때의 $\vec{w}$ 값입니다.

  • $\vec{w} = (\vec{x}^T \vec{x})^{-1}\vec{x}^T \vec{y}$

Least Square의 남아있는 문제점

Bias variable

원점을 지나지 않는 모델을 구해야 할 수 있습니다. 따라서 Bias를 고려해야합니다.

기존에 존재하던 데이터에 가상의 feature를 추가합니다.

• $\vec{x}= \begin{bmatrix} -0.1 \\ 0.3 \\ 0.2 \end{bmatrix} \rarr \vec{z}= \begin{bmatrix} 1 & -0.1 \\ 1 & 0.3 \\ 1 & 0.2 \end{bmatrix}$

이외의 문제들

• 정답이 한 개만 존재하는 경우가 많지 않음

• 역행렬을 계산할 수 없는 경우도 많음

• Outlier에 상당히 취약하게 동작함

• 데이터가 너무 클 경우 -> 벡터곱 혹은 역행렬 계산이 어렵습니다.

• x가 작을 때는 선형이었다가, x가 충분히 커지면 y가 더 이상 증가하지 않는 경우가 있을 수 있습니다.