[ML] 딥러닝의 깊이 있는 이해를 위한 머신러닝 6-2 (K-MOOC)

Linear Classification 문제 풀이 방법

Degenerate Solution을 쉽게 제거하는 방법

Hinge Loss

• $max(0, 1-y_i \vec{w}^T \vec{x_i})$

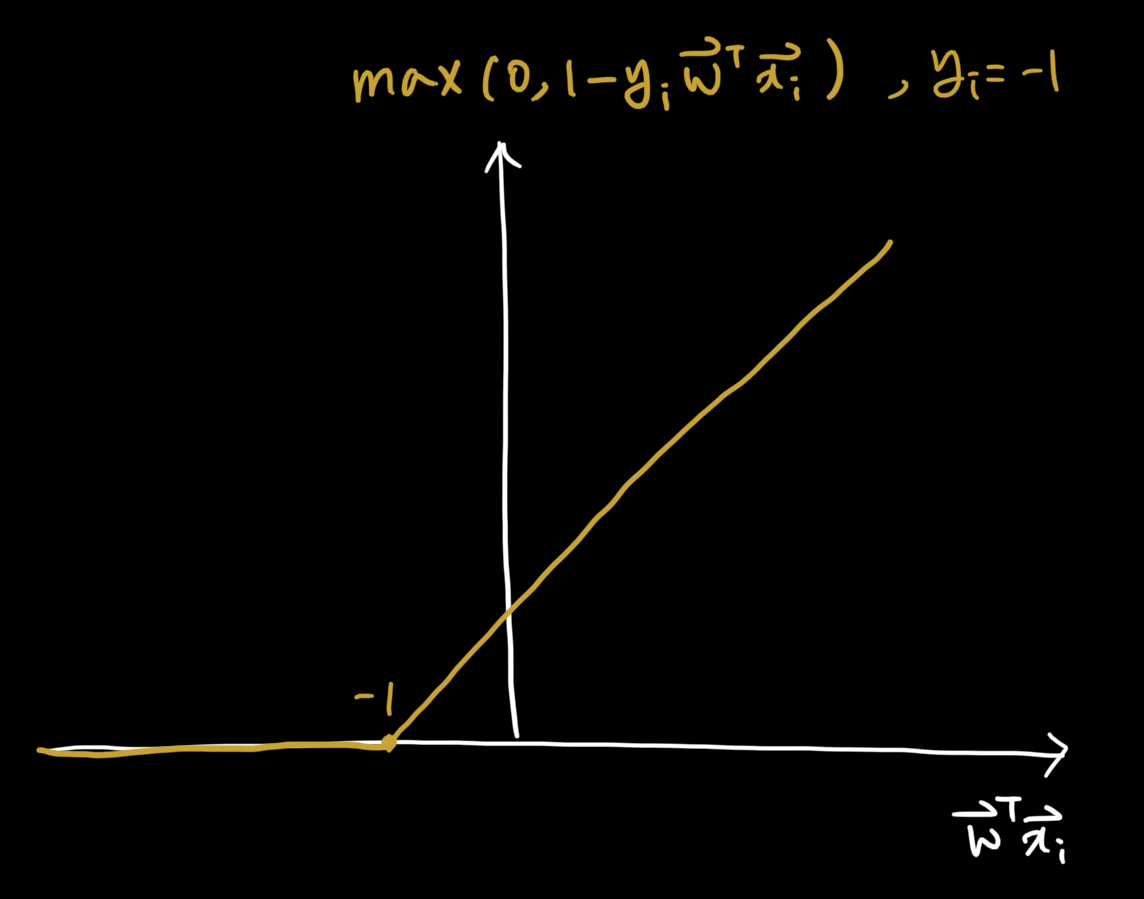
• 마진값(위 그림의 경우 마진값은 1입니다.)을 추가함으로 degenerate solution을 제거할 수 있습니다.

  • $\vec{w}$ 가 0 값을 가지면 loss function은 1 값을 가지므로 최소가 되지 못합니다. (loss를 최소로 줄여야 합니다.)

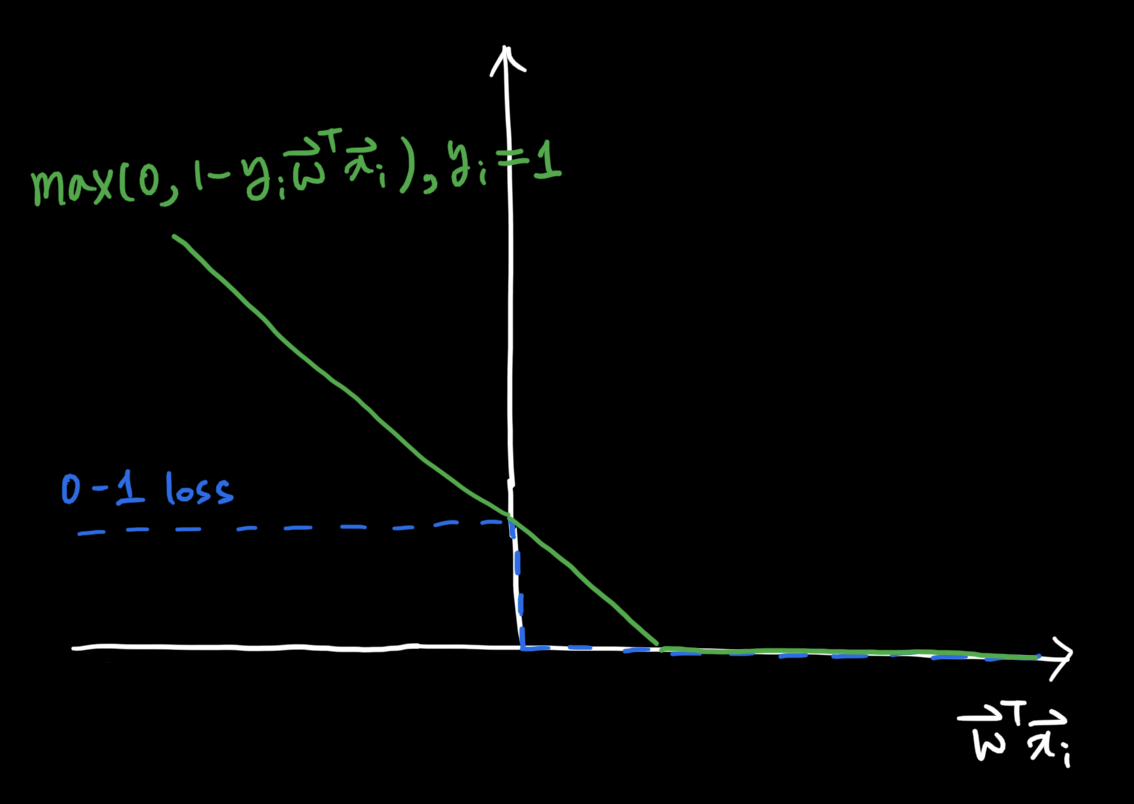
• 아래 그림은 0-1 loss function과 hinge loss function을 동시에 나타냅니다.

• hinge loss는 0-1 loss 보다 항상 크거나 같습니다.

• 정확하게 0-1 loss와 hinge loss가 일치하는 지점이 존재합니다.

• 그 외에는 모두 hinge loss가 0-1 loss보다 큰 영역을 가지게 됩니다.

• 힌지 로스는 Support Vector Machine(SVM)에서 정말 많이 사용됩니다.

• SVM

  • 힌지 로스에 w라는 L2 regularization term을 추가로 활용합니다. (regularizer는 추후에 자세히 다룬다고 합니다.)

• 힌지 로스는 Linear Classification 모델에서 좋은 성능을 내기 때문에 아직도 널리 사용됩니다.

Logistic Loss

$f(w) = \sum_{i=1}^{n} log(1 + exp(-y_i \vec{w}^T \vec{x_i}))$

• Max 함수를 Log-Sum-Exponential로 추정하여 변환합니다.

• 항상 미분이 가능하여 최소값을 구하기 쉽습니다.

• $y_i$와 $\vec{w}^T \vec{x}$의 부호가 다르고 곱한 값이 커지면 커질수록 loss도 어마무지하게 커질 것입니다. (수식에 대입해서 생각해보세요!)

• $max(0,-y_i \vec{w}^T \vec{x_i}) \approx log(exp(0) + exp(-y_i \vec{w}^T \vec{x_i}))$

• logistic loss가 문제점을 잘 해결하고 있을까요?

  • 미분 가능한가? -> O

  • degenerate solution이 없는가? -> O

• logistic loss VS hinge loss

  • hinge loss: $y_i$가 1일 때 $\vec{w}^T \vec{x_i}$가 1 이상이면 미분값이 0을 가집니다. -> 즉 $\vec{w}^T \vec{x_i}$가 1이상인 값에서는 최적화가 불가능 합니다.

  • logistic loss: 모든 영역에 대해서 미분 가능합니다.

Logistic Regression과 SVM의 장점

• 학습 또는 테스트의 속도가 빠릅니다.

• 너무 많은 데이터가 주어졌을 경우에는 데이터 중 일부만 고려하는 stochastic 방법 활용 가능

  • stochastic 방식의 대표적인게 deep learning입니다.

• $\vec{w}$를 쉽게 얻고, 이를 분석하기 좋습니다.

  • $w_i$의 크기가 크다면 해당되는 feature가 많이 고려되고 있음을 의미합니다.

  • linear classification 모델 학습 후 중요한 피쳐가 무엇인지 역으로 분석 가능합니다.

Probabilities로 구현할 수 있을까요? (위에서 다룬 것은 Predictions)

• $\vec{w}^T \vec{x_i}$ 값이 0과 1사이 값을 가지도록 만들면 확률값으로 활용할 수 있습니다.

  • 이를 기반으로 확률적 구분기를 만들 수 있습니다.

  • 하지만 Linear Regression 결과값은 어떤 범위 안에 가두기 어렵습니다.

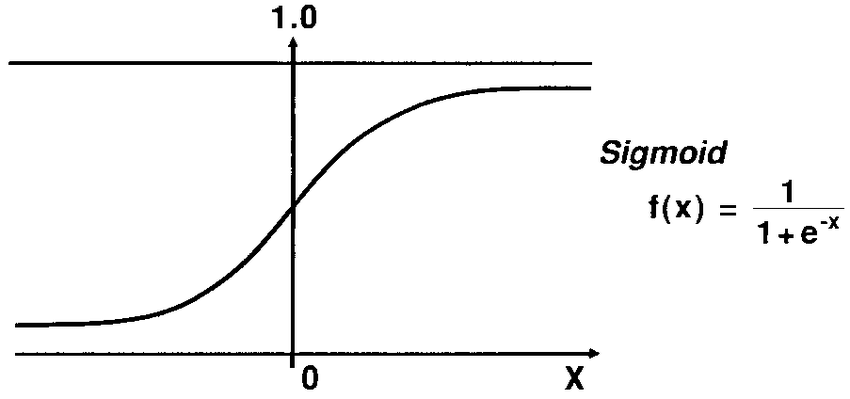
  • 바로 위 문장을 해결하기 위해 sigmoid function을 활용합니다.

  • Sigmoid function

    • $h(z_i)=\frac{1}{1+exp(-z_i)}$

    •