[ML] 딥러닝의 깊이 있는 이해를 위한 머신러닝 7-1 (K-MOOC)

학습 내용

• 데이터에 노이즈가 있으면 어떤 결과가 나올까?

• 노이즈에 강인한 학습 방법은 무엇이 있을까?

• RANSAC 알고리즘이란 어떤 것일까?

Least Squares with Outliers

• Least Squares는 아웃라이어에 취약하다는 특징을 보여줍니다. (아래 그림 참고)

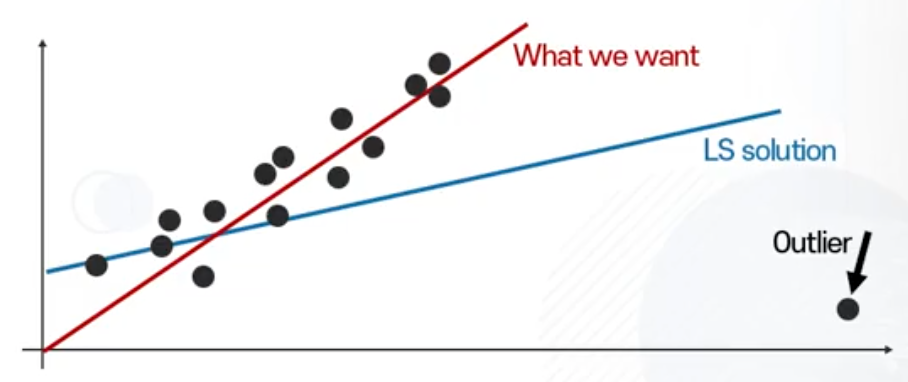
• Least Square에서 노이즈에 취약하게 반응하는 이유

  • 미분을 통해서 결과값을 얻는 방법론은 접근 불가능

  • 에러가 커질수록 Cost가 기하급수적으로 커집니다.

  • 상대적으로 에러가 큰 값들을 위주로 줄이려고 합니다.

    • 큰 에러에서 로스 값이 훨씬 크기 때문입니다.

  • 대표적인 해결방법: L1-Norm

    • 에러가 커지더라도 줄여야 되는 로스 값은 똑같은 수식이 주어진다면???

    • 절대값을 활용합니다.

      • $f(\vec{w}) = \sum_{i=1}^{n} | \vec{w}^T \vec{x_i} - y_i |$

    • 하지만 미분이 불가능합니다... (절대값은 뾰족하니까)

    • 절대값 함수를 추정하여 미분 가능한 함수로 변환해야 합니다.

• Robust Regression with L1-Norm

  • Huber Loss: Absolute 에러와 Least Square의 장단점을 합친 것입니다.

    • 엡실론 값보다 작으면 Least Square 에러 (Least Square -> 모든 영역에서 미분 가능)

    • 엡실론 값보다 크면 Absolute 에러 (Absolute 에러 -> 아웃라이어에 강인함)

    • $f(\vec{w}) = \sum_{i=1}^{n} h(\vec{w}^T \vec{x_i} - y_i)$

    • $h(r_i) = \begin{cases} \frac{1}{2}r_i^2 & \text{,for $|r_i| \leq \epsilon$}\\ \epsilon (|r_i| - \frac{1}{2} \epsilon) & \text{,otherwise} \end{cases}$

• Infinite Norm Regression

  • 노이즈가 있는 데이터에 관심을 가지는 리그레션 모델인 경우 활용해야 하는 에러는?

  • 최대값을 최소화하는 방향으로 로스를 설계하면 됩니다.

    • $f(\vec{w}) = ||\vec{w}^T \vec{x_i} - y_i||_{\infin}$

    • where $||r||_{\infin} = \underset{i}{max}(|r_i|)$

    • 로스 최대값을 가지는 샘플의 로스를 최소화하는 방향으로 리니어 모델을 얻는다면 노이즈에 관심을 가지는 새로운 형태의 리그레션 모델을 얻을 수 있습니다.

    • 참고: $\underset{i}{max}(|z_i|) \approx log(\sum_{i} exp(z_i))$

RANSAC

• 노이즈가 꽤 많은 비중으로 존재하여 아웃라이어의 정보들을 무시해야 하는 경우 활용됩니다.

• 1-norm 리그레션의 경우 아웃라이어가 로스에 영향을 미치기는 합니다.

• 아웃라이어 값들을 아예 배제할 수 있을까? -> RANSAC

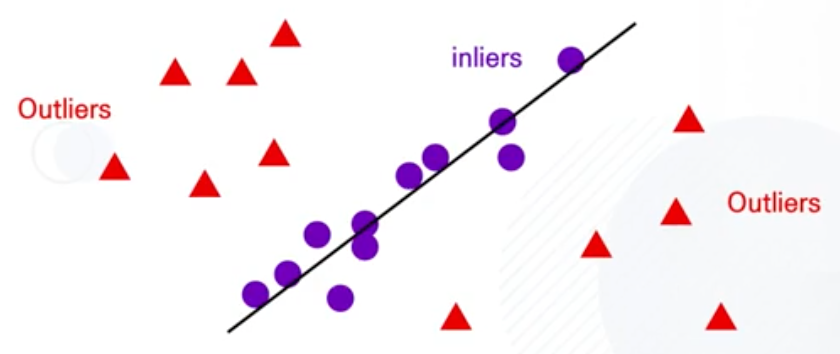
• RANSAC 작동과정

  1. 처음 주어진 학습 데이터 중 일부분만 선택

  2. 선택된 샘플들 만으로 리니어 리그레션 모델을 계산

  3. 계산된 Linear Regression 모델로 인라이어/아웃라이어 구분

  4. 위 과정을 반복

  5. 가장 많은 인라이어를 갖는 Linear Regression 모델을 최종 선택

     • (가정에서 "샘플들 중 인라이어가 대다수 일 것이다." 라고 했습니다.)

• RANSAC의 장점

  • 아웃라이어를 무시하고 인라이어만 고려할 수 있습니다.

  • 컴퓨터 비전, 음성 인식, 실제 머신러닝 알고리즘들에서 다양하게 활용되고 있습니다.