Entropy, Cross Entropy, KL-Divergence

  이 글은 cs231n 3강을 복습하다가 모르는 부분들을 찾아보고 정리한 내용이다. 공부를 하다보면 많이 듣게되는 Entorpy/ Cross Entropy/ KL Divergence를 다룰 예정이다. 대충은 뭔지 알지만 설명하라고 하면 못할 것이기 떄문에, 한 번쯤 제대로 정리할 필요는 있다고 생각했다.

1. Entropy

  정보 이론에서의 Entropy는 정보를 최적으로 encoding 하기 위해 필요한 bit 수, 혹은 정보량의 기댓값이다. 말로만 설명하면 무슨 말인지 헷갈리니 예시를 들어 살펴보자. 주사위 1개를 bit로 표현한다고 하자. 주사위는 6까지 있기 때문에 6개의 서로 다른 표현 방식이 필요하다. bit는 0 혹은 1로 나타내기 때문에, 우리는 3 bit가 필요하다. 2의 세제곱=8 이기 때문에 6개를 담을 수 있다. 이렇게 정보를 나타내기 위해 필요한 bit수를 구하는 공식을 쓰면,

  위 사진과 같은 공식을 얻을 수 있다. 본격적으로 entropy를 살펴보기 전에 정보량부터 알아야 한다.

1) 정보량

  정보량은 정보 이론의 기본 단위이며, 놀람의 정도라고 생각하면 된다. 식이 설계된 컨셉은 이렇다. 발생확률이 큰 것은 bit의 개수를 적게 해서 표현하고, 발생확률이 작은 것은 bit의 개수를 늘려서 표현하는 것이다. 이렇게 하면 모든 정보를 비슷한 bit 개수로 표현하는 것보다 이득을 볼 수 있다고 한다. 공식은 아래와 같다.

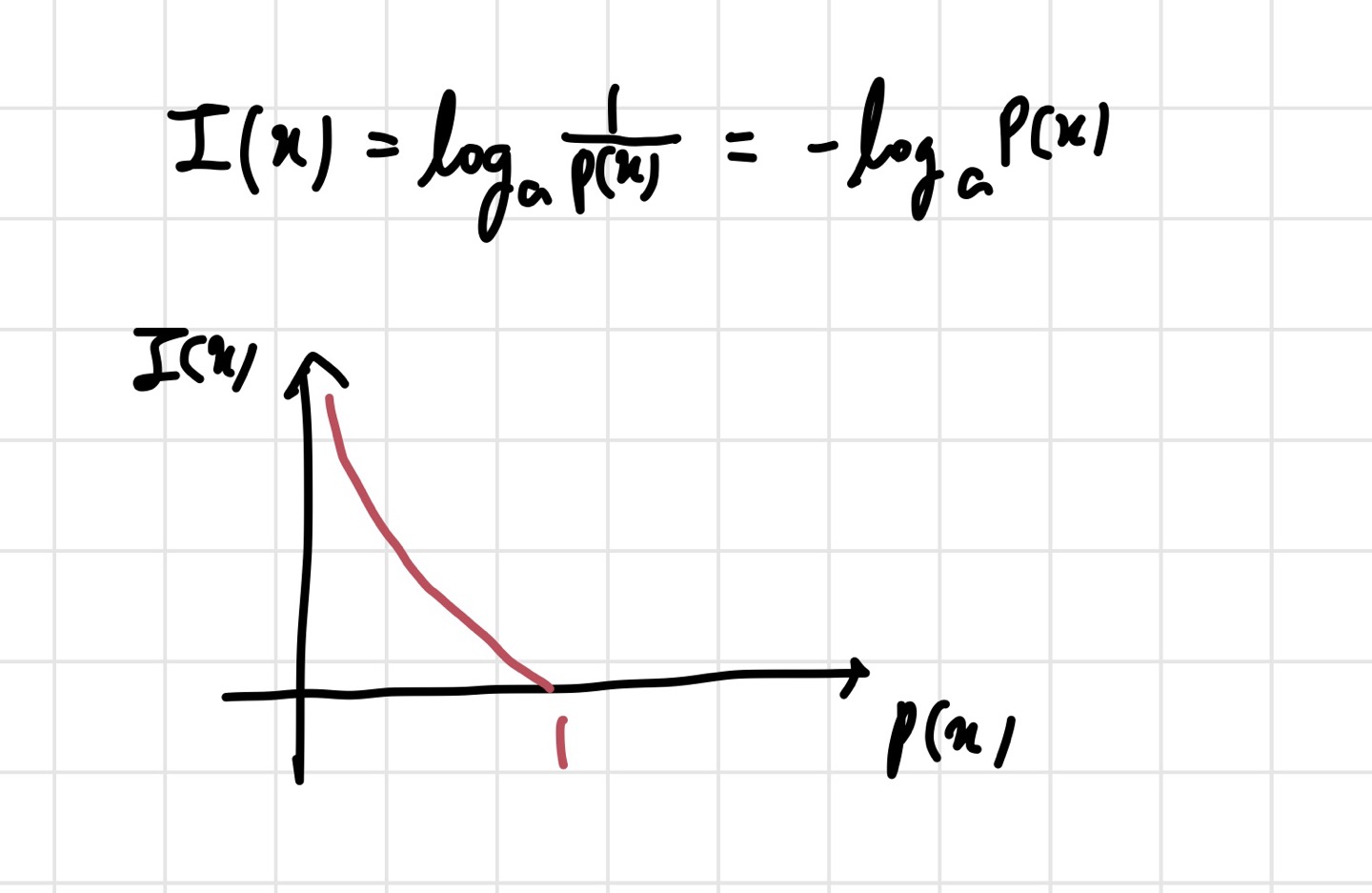
  보통 bit를 구해야 하기 때문에 a값은 2를 많이 쓴다. 여기서 $x$는 어떤 사건을 의미하고, $p(x)$는 사건 $x$가 일어날 확률을 의미한다. $log$ 안에 $p(x)$가 아니라 $1\over p(x)$ 이 들어간 이유는 위 사진의 그래프를 통해 이해할 수 있다. 기본적인 컨셉은 발생확률이 큰 것은 적은 bit수로 표현하는 것이었다. $1\over p(x)$를 사용해 이게 가능해진 것이다. 그래프를 보면 $p(x)$가 커질수록 정보량은 줄어든다. 우리가 원하는 바를 이룬 것이다. 다시 한 번 정리하자면, 확률이 적은 사건(잘 일어나지 않는 사건)이 일어났을 때 많이 놀란다는 것(정보량이 많다는 뜻)이다. 이를 바탕으로 entropy를 살펴보자.

2) Entropy

  Entropy의 공식은 아래 사진과 같다.

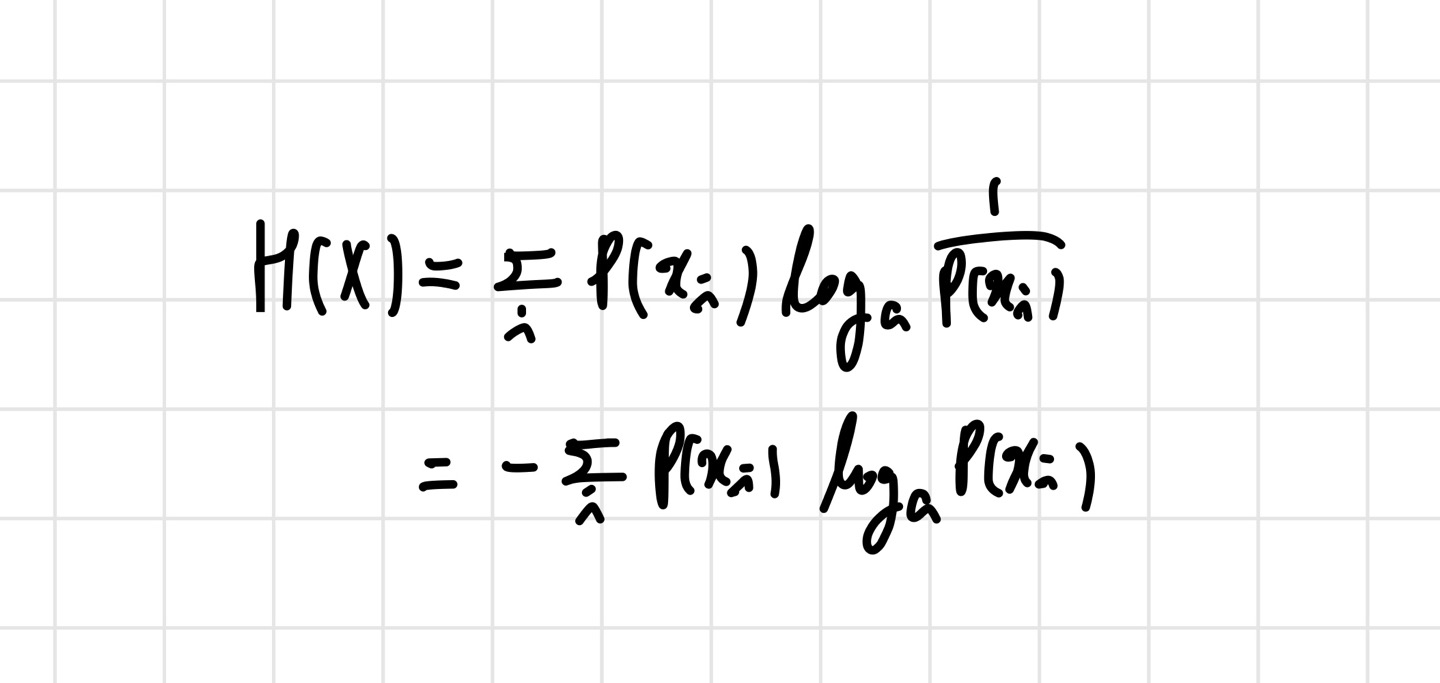
여기서도 보통 a=2를 많이 사용한다. 엔트로피는 $H(X)$로 표현하며, $X$는 확률 랜덤 변수를 의미한다. 정보량의 평균이라고 정의했기 때문에 위와 같은 식이 나온 것이다. 이것도 예시를 통해 알아보자. 윷놀이의 엔트로피를 구해보겠다. 여기서 나올 수 있는 경우의 수는 {도, 개, 걸, 윷, 모} 이다. 각각의 확률을 구해 식에 대입하면 된다.

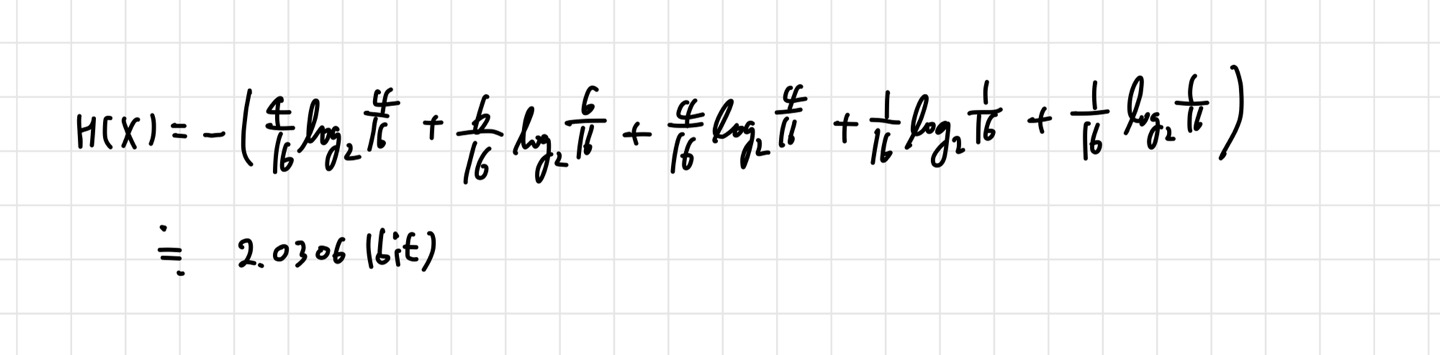
  이렇게 엔트로피를 구할 수 있는 것이다. 이제 Cross Entropy를 살펴보자.

2. Cross Entropy

  지금까지는 하나의 확률분포 $P(x)$에 대해서만 살펴봤다면, 이제는 확률 분포 $Q(x)$도 등장한다. $P(x)$는 이상적인 확률 분포, $Q(x)$는 우리가 모델링해서 얻은 확률분포이다. Cross Entropy는 $P(x)$와 $Q(x)$를 비교했을 때, 즉 이상적인 값(정답 값)과 예측값이 달라서 생기는 정보량인 것이다.

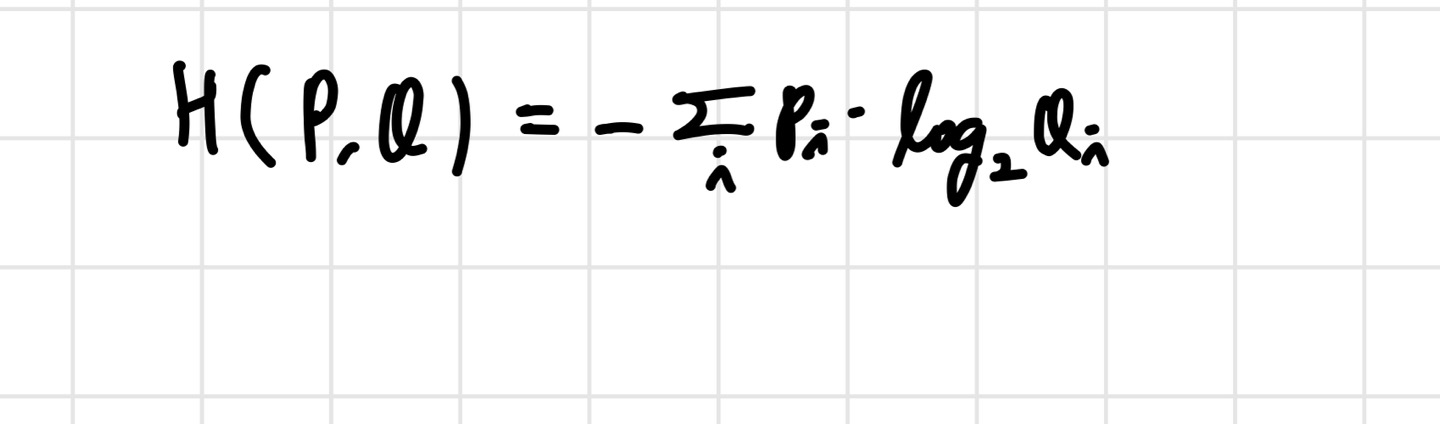
  엔트로피와 비슷한 형식의 공식이지만, $Q_i$만 들어갔다고 생각하면 된다. 이걸 loss function으로 이용하면 머신러닝이나 딥러닝에 적용시킬 수도 있다. cross entropy 값이 0이 되는 쪽으로 모델을 학습시키면 우리의 예측값이 정답값에 가까워질 것이기 때문이다. 그렇다고 모든 경우에 좋은 성능을 내는 것은 아니다. classification 문제에서 좋은 성능을 내는 경향이 있긴 하다.

3. KL Divergence

  KL Divergence는 두 분포가 얼마나 비슷한가에 대한 답을 주는 개념이다. 어려운 말로 하면 이상적 분포 $P$에 대해 그 분포를 근사하는 다른 분포 $Q$(우리가 모델을 통해 얻은 분포)를 샘플링 한다면 얻을 수 있는 정보량의 차이라고 표현할 수 있다. 그런데 나한테 더 와닿았던 것은 '두 분포가 얼마나 비슷한가' 라는 표현이다. KL Divergence 식은 cross entropy로부터 유도할 수 있다.

  어느 정도 정의와 비슷하게 식이 나오는 것을 알 수 있다. 중요한 KL DIvergence의 특성으로는,

i) KL(P||Q) >0
ii)KL(P||Q)!=KL(Q||P) (두 식이 같지 않다는 뜻이다.)

이렇게 두 가지 정도가 있다.
일단 이 정도로 정리하고, 나중에 더 보충할 개념이 있다면 추가하려고 한다.

3. 참고

이번 글은 아래 블로그를 참고해서 작성했다.
https://angeloyeo.github.io/2020/10/27/KL_divergence.html

https://angeloyeo.github.io/2020/10/26/information_entropy.html