Jacobian Matrix

  이번에는 cs231n 4강을 복습하다가 모르는 내용이 나와서 정리를 해보려고 한다. Jacobian matrix는 backpropagation에서 많이 사용되는 내용이다. 각 변수에 대한 partial derivative를 알려주기 때문에 유용하게 사용할 수 있다. 그런데 Jacobian matrix가 나온 이유를 알기 위해선 Linear transformation부터 알아야 한다.

1. Linear Transformation

  선형대수에서 가장 중요한 주제 중 하나로 꼽히는 내용이다. 행렬을 어떤 관점으로 볼 지에 대한 intuition을 주기도 한다. 먼저 transformation은 function을 좀 멋지게 쓴 말이다. 굳이 다른 표현을 쓰는 이유는 느낌이 달라서이다. transformation을 하면 벡터를 움직여서 다른 output을 주기 때문이라고 한다. 뭐 그렇게 중요한 얘기는 아니다. 알아야 할 것은 어떤 벡터를 받으면 다른 벡터를 뱉는 함수라는 것이다. Linear라는 단어는 transformation 이후에도 grid line들이 평행하고 evenly spaced인 상태여야 한다는 것을 뜻한다.
 일단 기본적인 컨셉은 이런데, 언제나와 같이 수학적으로 이 내용을 표현할 방법을 알아야 한다. 어떤 vector space에 있는 모든 벡터들을 transformation 했을 때 어떻게 바뀔지를 표현해야 한다는 뜻이다. 답은 간단하다. basis vector들을 이용하면 된다. vector space의 모든 vector들은 basis vector들의 linear combination으로 표현될 수 있기 때문에, basis vector들이 어떻게 바뀌는지만 표현해주면 transform된 vector space의 모든 벡터들을 표현할 수 있을 것이다. 예시를 들어서 이해 해보자.

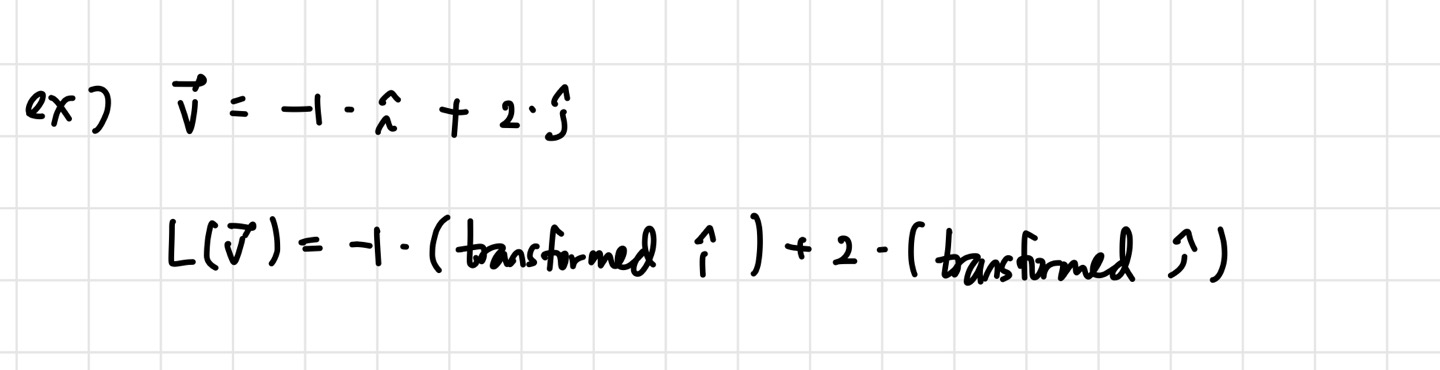
  벡터 v가 있다고 해보자. 만약 vector space의 basis가 2개라면 basis vector $i,j$에 대한 선형 결합으로 표현할 수 있을 것이다. 이 vector를 transform 시킨 벡터 $L(v)$도 바뀐 $i,j$만 알면 선형결합으로 나타낼 수 있다는 말이다.

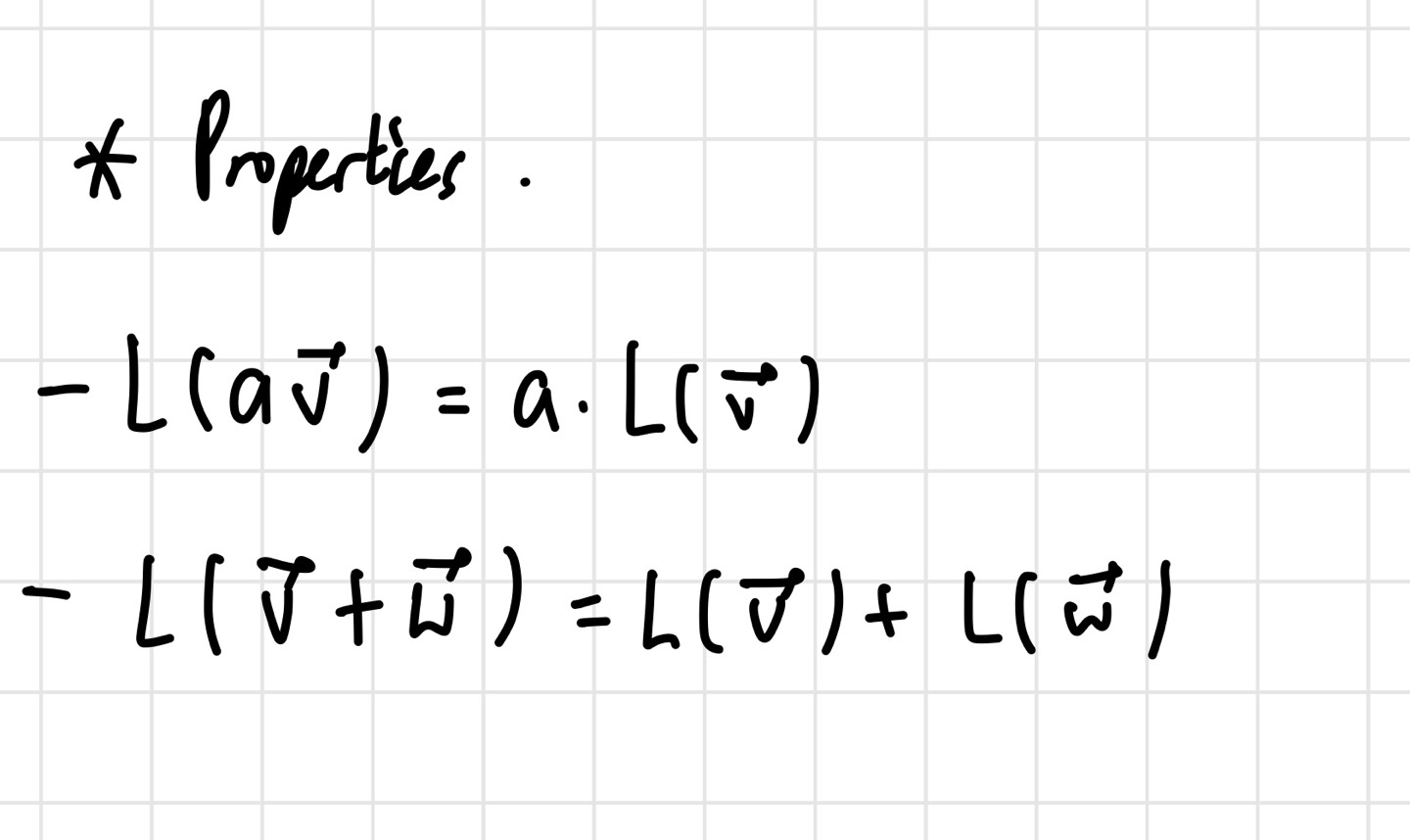
  기본적으로 Linear transformation이 가지는 property들이다. 위의 예시도 이 property들을 따르는 것을 알 수 있다. 이제 우리가 할 일은 basis vector들이 어디로 가는지만 알아내는 것이다. 아래 사진은 각각의 basis vector들이 (a,b), (c,d)로 이동했다고 가정하고, 이를 2x2 matrix로 만든 것이다.

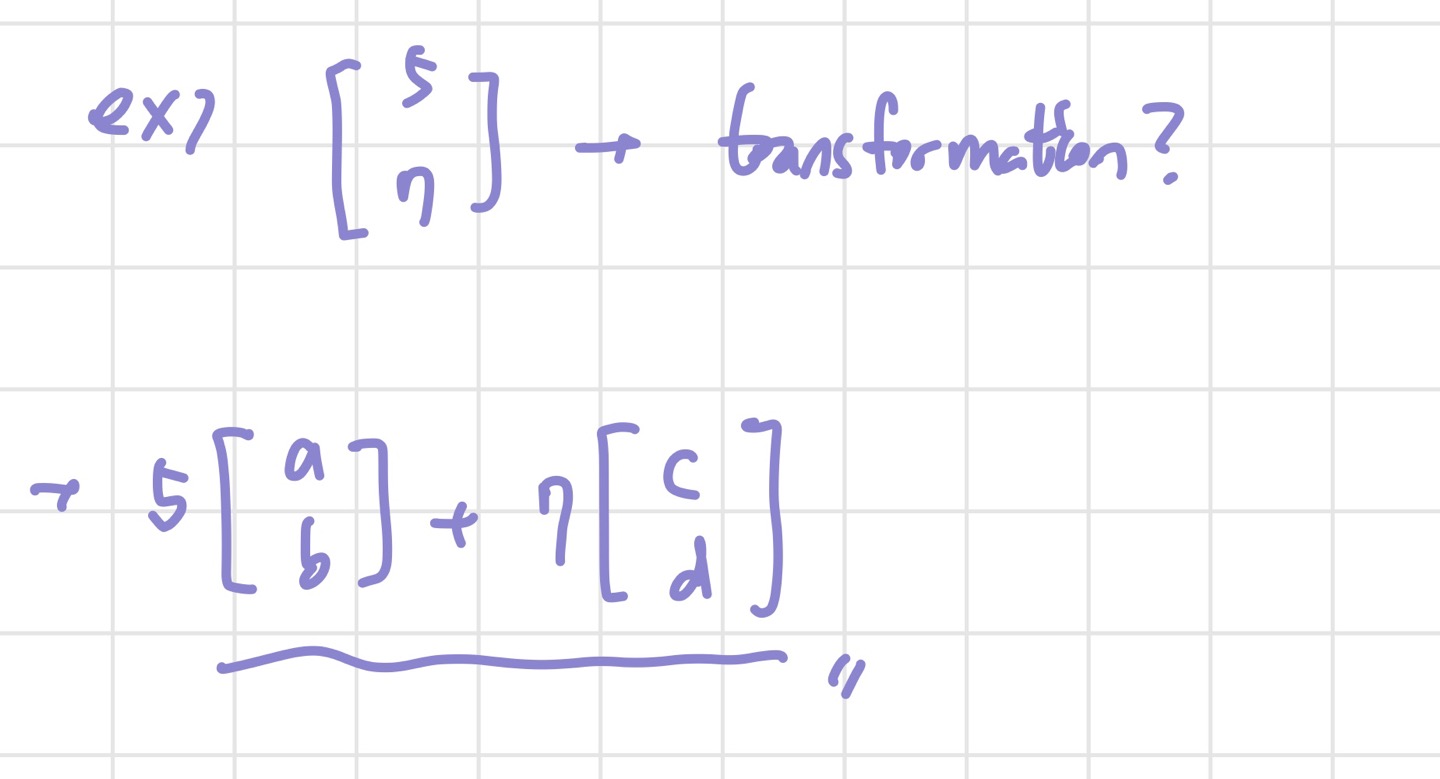
  이를 바탕으로 (5,7)이 transform 후에 어떤 벡터가 될지 표현한 것이다. transform된 basis vector들의 linear combination으로 나타낼 수 있다.
 지금까지 Linear transformation이 무엇인지 대략적으로 살펴보았다. 그러나 우리의 목적은 Jacobian matrix를 이해하는 것이다. Linear Transformation과 Jacobian matrix는 어떤 관계가 있을까?

2. Jacobian Matrix

  Jacobian matrix는 기본적으로 각 변수들의 partial derivative를 적어놓은 행렬이다. nonlinear 한 function의 tranformation을 하자니 너무 복잡하니까, nonlinear function이 linear하게 보일 때까지 확대해서 linear transformation을 하는 것처럼 생각하자는 것이다. 이런 아이디어로 만들어진 것이기 때문에, 당연히 미소구간을 살펴보는 것이다. 미소구간 하면 생각나는 것이 미분이고, 여러 변수들이 있기 때문에 편미분을 이용해 linear function을 표현하는 것이다. 이것도 예시를 통해 알아보자.

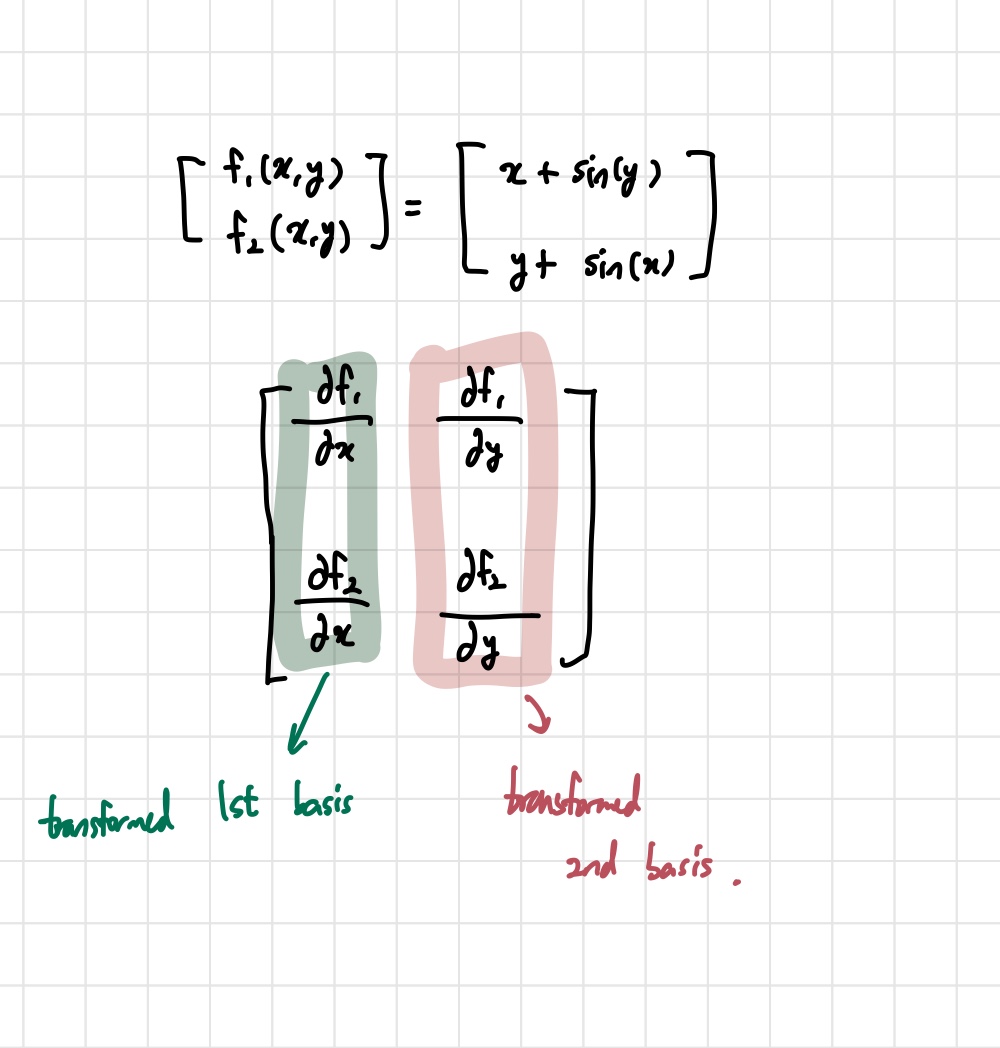
  위와 같이 2개의 변수로 이루어진 벡터가 있다고 해보자. 이들의 Jacobian matrix는 위에 편미분으로 이루어진 행렬이다. Linear transformation에서 봤듯이, 각 열은 basis가 어디로 transform 되었는지에 대한 정보를 알려준다. 이를 계산해본다면 아래 사진처럼 나올 것이다.

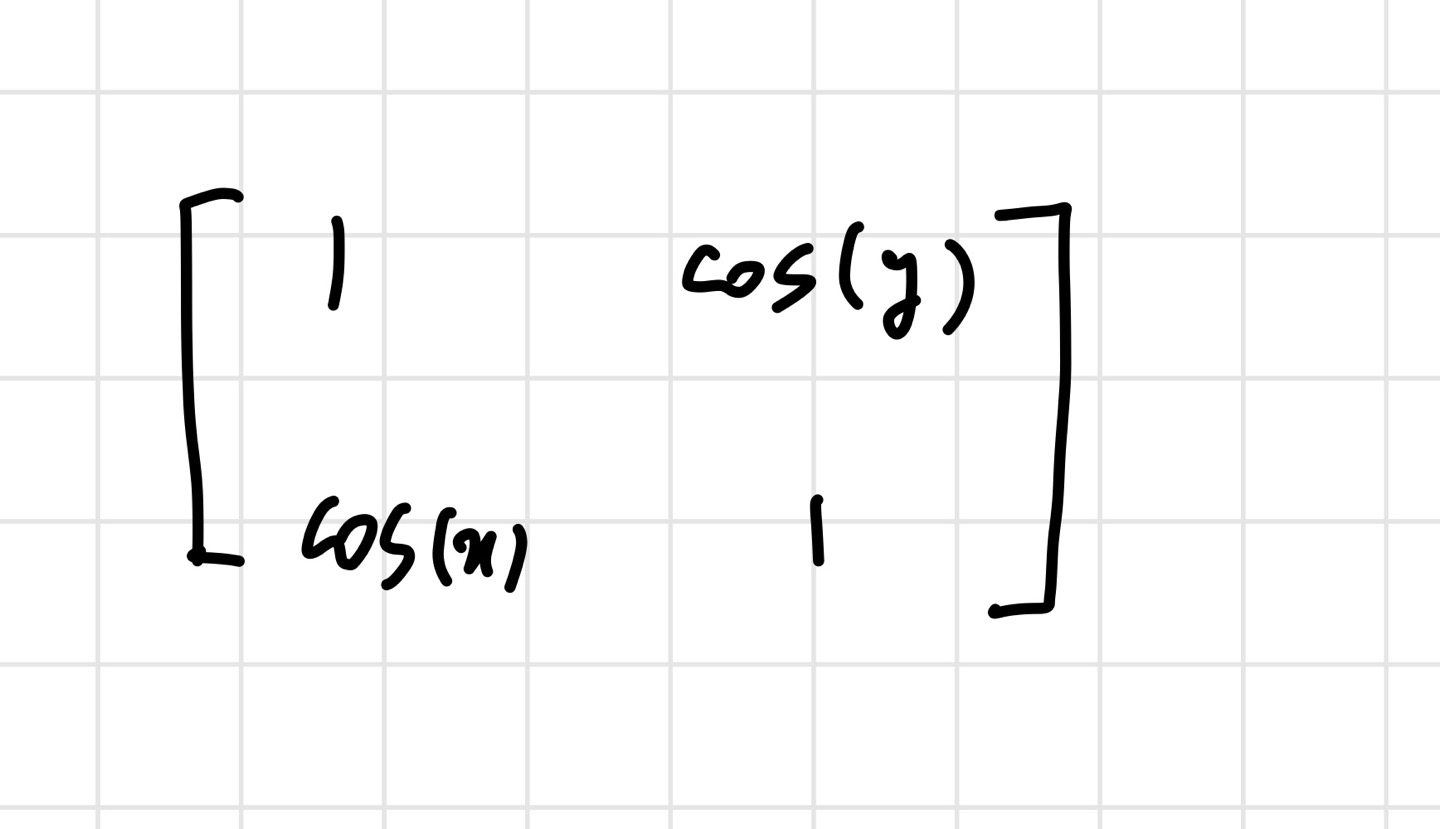
이 행렬이 뜻하는 바를 해석해보자. 첫 번째 basis는 transform 결과 (1,cos(x))가 되었다. 이것을 이용하면 transform된 다른 벡터들도 다 표현 가능할 것이다.

3. 참고 자료

  이번 글은 Khan academy의 강의를 많이 참고해 적었다.
https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivatives/jacobian/v/the-jacobian-determinant