1. 2강 복습
간단히 2강에서 다룬 내용을 복습하고 넘어가자. 주요한 주제들은 KNN, Linear classifier 가 있었다. 그 중에서 KNN은 영상처리에는 적합하지 않았고, Linear classifier는 Neural Network를 이루는 것이라고 하니, 잘 알아둘 필요가 있다는 것을 배웠다. 그런데 Linear Classifier에서 가장 좋은 W(가중치)를 찾는 것이 문제였고, 이것에 대한 해결책을 3강에서 다룬다.
2. Loss Function(손실함수)
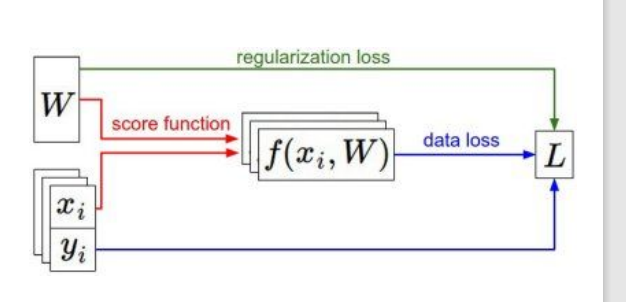
Loss Function은 기계학습에서도 다루는 내용이다. 그렇지만 그것보단 조금 더 깊게 들어간다. Loss function은 현재 우리의 classifier가 얼마나 좋은지에 대한 지표를 알려준다.
 위 사진의 data set 부터 살펴보자. i는 현재 몇번째 데이터인지를 나타낸다.i의 범위가 1부터 N이므로, 이 데이터 셋은 데이터 개수가 N개인 것이다. 또, x_i는 input data, 즉 영상처리에서는 영상에 해당한다. 그리고 y_i는 정수값 라벨이다. 이전에 살펴본 CIFAR-10에 경우, 클래스가 10개이므로 y_i의 범위는 0~9로 할당해 각 클래스를 표현하는 것이다. 그리고, 아래의 식은 각 데이터를 손실함수에 넣어 L_i를 구하고, 그것들의 합을 평균으로 나누어 최종 Loss를 얻는 식이다. Loss function은 우리가 정하기 나름이라, 뒤에 나올 Multiclass SVM Loss와 Softmax function을 통해 자세히 알아보자.
위 사진의 data set 부터 살펴보자. i는 현재 몇번째 데이터인지를 나타낸다.i의 범위가 1부터 N이므로, 이 데이터 셋은 데이터 개수가 N개인 것이다. 또, x_i는 input data, 즉 영상처리에서는 영상에 해당한다. 그리고 y_i는 정수값 라벨이다. 이전에 살펴본 CIFAR-10에 경우, 클래스가 10개이므로 y_i의 범위는 0~9로 할당해 각 클래스를 표현하는 것이다. 그리고, 아래의 식은 각 데이터를 손실함수에 넣어 L_i를 구하고, 그것들의 합을 평균으로 나누어 최종 Loss를 얻는 식이다. Loss function은 우리가 정하기 나름이라, 뒤에 나올 Multiclass SVM Loss와 Softmax function을 통해 자세히 알아보자.
3. Multiclass SVM Loss
이것도 기계학습 과목에 나오는 내용을 확장한 것이다. 기계학습에서도 SVM을 배운다. '그럼 지금 하는 것과 다른 것이 무엇인가?' 라는 질문이 나올 수 있다. 그때는 주로 binary class, 즉 클래스가 2개인 데이터를 다루는 반면, 지금은 클래스가 2개 이상인 것이 가장 큰 차이점이다. 말이 어려워 보이지만 사실 크게 다를 것은 없다.

일단 Multiclass SVM loss의 식은 이렇게 되는데, 어려워 보여도 차근차근 살펴보면 이해가 된다. 먼저 각 변수들이 무엇을 의미하는지부터 보자.
-
: correct class score (해당 데이터의 맞는 클래스의 점수이다.)
-
: incorrect class score(맞는 클래스 빼고 나머지 클래스들의 점수이다.)
여기서 s는 linear classifier에서 나온 score vector를 의미한다.
이제 식을 살펴보자. 로 나올 수 있는 값은 0 아니면 이다. 우리가 추구해야 하는 건 손실이 최대한 안 나야 하는 것이기 때문에, Loss function을 최소화 하는 것이 목표이다. 그렇기 때문에 저 두 값 중에 0이 많이 나오면 나올 수록 좋은 것이다. 그럼 각각 어떤 경우에 저 두 값이 나오는지 살펴보자. 먼저, 0이 나오는 경우는 인 경우다. 식을 해석해보면 정답 클래스의 점수가 오답 클래스의 점수+1 보다 크면 손실이 0인 것이다. 여기서 1은 safety margin이다. 정답 클래스의 점수가 오답 클래스의 점수보다 안정적으로 클 수 있도록 해주는 파라미터인 것이다. safety margin의 값은 경우에 따라 바뀔 수 있다. 그리고, 반대로 (정답 클래스의 점수)<(오답 클래스의 점수+1) 이면, 손실을 계산한다. 이것이 Multiclass SVM Loss에서 Loss 를 계산하는 방법이다.

위의 사진에서 그래프의 x축: , y축: loss를 의미한다.
Multiclass SVM loss는 Hinge Loss라고도 한다. 그래프를 그려보면 힌지같이 생겨서 그런 것 같다. 이렇게 각각의 data에 대한 loss L_i를 구한 다음 평균을 내면 그것이 최종 L값이 된다.
Multiclass SVM을 사용할 때 중요한 디버깅 테크닉도 알아볼 필요가 있다. 코딩을 할 때 first iteratrion에서는 아직 아무것도 모델이 학습하지 않았기 때문에 s값들이 다 0에 가까울 것이다. 이때의 Loss는 (class 개수-1)이 된다. 만약 반복문이 한 번 돌고 나서 나오지 않는다면, 내 코드에 뭔가 문제가 있는 것이다.
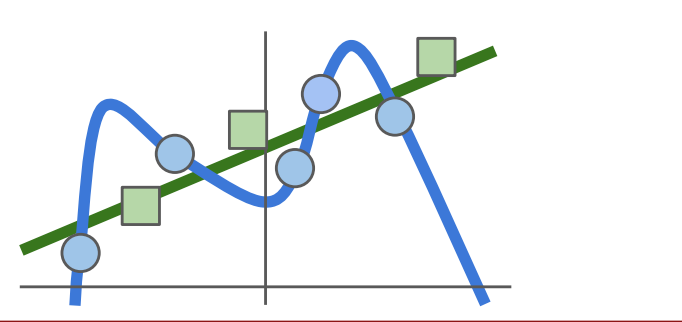
이렇게 해서 L=0으로 만드는 W를 찾아냈다고 치자. 내가 찾아낸 W가 유일한(unique) W일까? 2*W도 답이 될 수 있을 것이다. 그렇기 때문에 우리는 어떤 W를 골라야 할지에 대한 혼란이 생긴다. 이러한 혼란은 우리가 train data에 초점을 맞추고 W를 고르려고 하고 있기 때문에 생긴다. 모든 모델의 목적은 새로 들어오는 test data를 잘 분류하는 것이다. 그렇기 때문에 test data에서 성능이 잘 나오는 W를 고르면 되는 것이다. 그런데, train data를 통해 훈련시킨 모델이 test data에는 너무 복잡한 경우가 많이 생긴다. 이런 경우에 우리는 regularization을 이용해 모델을 좀 더 간단히 만들 필요가 있다.
4. Regularization

Regularization은 Loss function 뒤에 붙여서 사용한다. 물론 이것도 종류가 여러 가지 있으며, 문제 상황에 따라 L1,L2, dropout, max norm regularization 등 다양한 regularization term 중 적합한 것을 골라서 사용하면 된다. 여기서 람다는 regularization의 강도를 의미한다. 강도가 높으면 모델을 더 간단히 만드는 것이다. 위 언급한 방법 중에 L1,L2 규제화만 살펴보자.
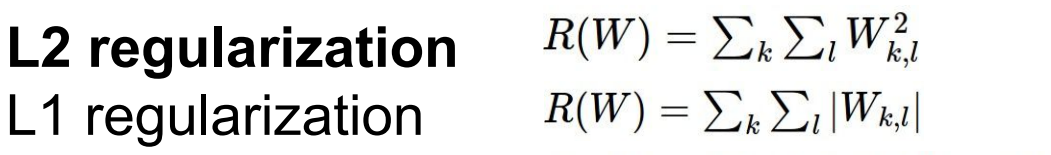
식은 위의 사진과 같이 나오고, 각각 weight vector의 원소들을 제곱하냐, 그냥 절댓값 해서 더하냐 차이다. L1, L2 norm의 개념에서 착안해서 이름도 L1,L2 reg. 인 것이다.

L2 규제화의 경우, x의 각 feature에 noise가 있거나, feature가 서로 연관되어 있어 고르기 어려운 경우 적용한다. w2를 보면, 모든 feature가 균등히 적용되는 것을 볼 수 있다.
L1 규제화의 경우, 특정 가중치를 삭제해 모델의 복잡도를 낮추는 효과가 있다. 그래서 w1을 보면, 학습 가중치가 하나의 feature에 집중되게 된다. 더 자세한 설명은 아래 링크에 정리해 놓았다.
https://velog.io/@danlee0113/L1-L2-Regularization
5. Softmax Classifier(Multinomial Logistic Regression)
이제 또 다른 loss function인 softmax function에 대해 알아보자. softmax의 기본적인 컨셉은 score vector s를 가지고 확률 분포를 만든다는 것이다. 이름이 softmax classifier라서 softmax만 가지고 loss를 계산하나? 라고 생각할 수 있지만, 사실 데이터를 softmax function에 태워서 확률 분포를 예측하고, cross entropy loss를 사용한다. cross entropy 공식에서, P는 우리가 가지고 있는 data의 ground truth label들이고, one hot encoding을 한 벡터들로 이루어져 있다. 그리고 Q가 우리가 softmax function을 통해 얻은 데이터의 확률분포가 되는 것이다. cross entropy를 통해 이 두 분포의 차이를 계산하고, 이 값을 최대한 낮추는 것이 우리의 목표인 것이다.
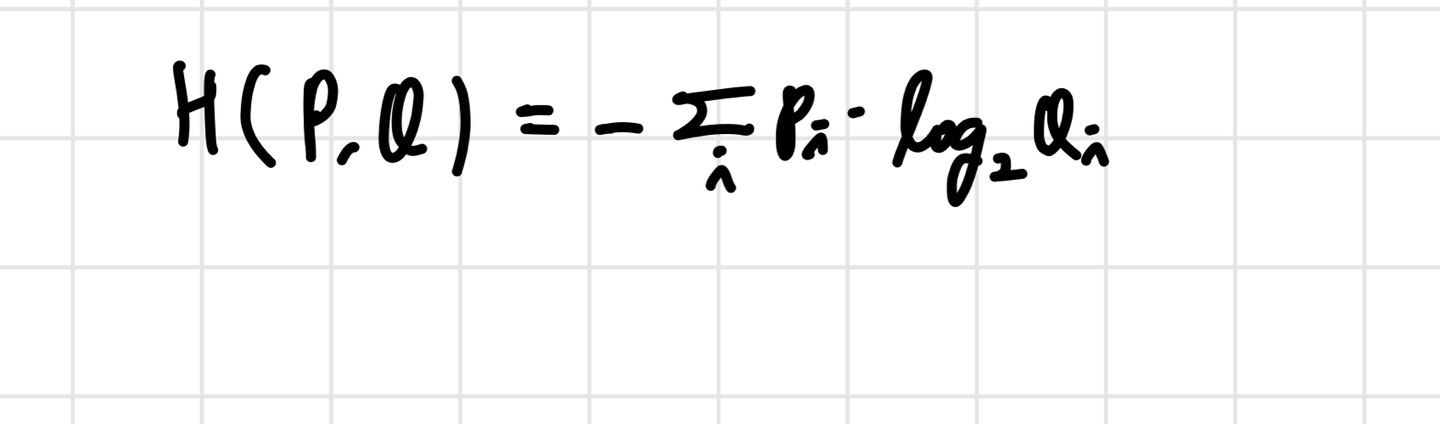
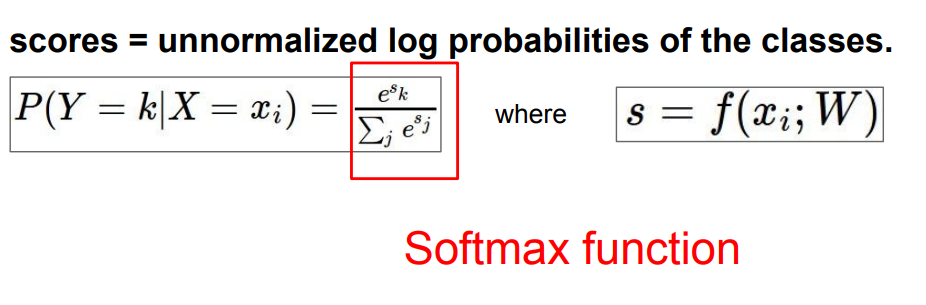
위 식을 보면, s를 일단 exponentiate시킨 후, exponentiate 시킨 값을 모두 더해 각각 class가 거기서 차지하는 비율을 따진다. 말이 어렵지만 그냥 클래식한 확률의 정의랑 똑같다. 결국 따지고 보면 (A가 일어날 경우의 수)/(모든 경우의 수)와 같은 형태라는 것이다. 이 식에 최대 우도법을 적용해 손실함수를 만든다.

최종적으로 정리하면 손실함수는 위와 같이 나온다. 갑자기 (-)가 붙은 이유는 간단하다. 손실함수는 최소화하기 때문에, 최대우도법에 마이너스 부호를 붙인 것 뿐이다.

여기서도 위의 SVM과 같이 디버깅 테크닉을 생각해볼 수 있다. 마찬가지로 first iteration이 끝났을 때를 생각해보자. 처음에는 s가 모두 0에 가까울 것이므로, 반복문을 한 번 돌고 나서의 loss=logC이어야 한다. (C: number of classes) 만약 logC가 나오지 않는다면, 내 코드는 잘못된 것이다.
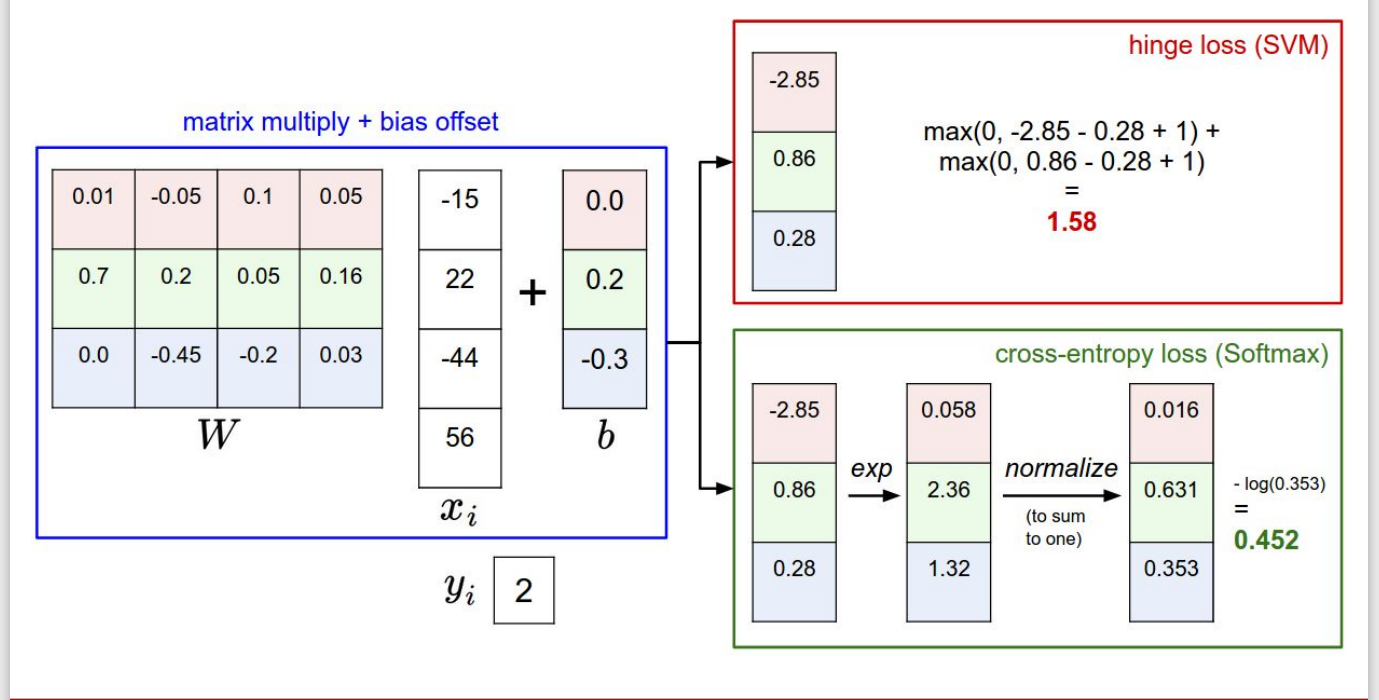
6. Softmax VS SVM
이제 두 가지 손실함수의 차이가 무엇인지 알아보자. SVM의 경우, 정답 클래스의 점수가 오답 클래스의 점수+1보다 크고 나면, 그 이후는 신경쓰지 않는다. SVM에서는 그저 safety margin보다 정답 클래스 점수가 크기만 하면 되는 것이다. 반면 Softmax는 확률 값을 다루기 때문에, 점수가 높을 수록 좋다. 그리고 각 클래스 별로 확률을 얻기 때문에 softmax classifier가 얼마나 결과에 대해 확신하는지에 대한 confidence를 알 수 있다. 그러나 실제로 두 손실함수를 사용할 때는 성능차이가 드라마틱하게 나진 않는다고 한다. 이 두 식이 어떻게 다르고, 어떻게 작동하는지만 알아두자.
7. Optimization
앞에서 손실함수도 배우고, 그 두 개의 식을 비교하기도 해봤다. 그럼에도 아직 우리는 손실함수를 최소화하는 W를 찾는 방법은 배우지 못했다. 그것을 해결해주는 파트가 Optimization(최적화)이다.
먼저 우리가 배경지식 없이 생각했을 때 어떤 방법으로 W를 찾을 수 있을지 생각해보자. 그냥 무턱대고 random search를 해서 노가다를 통해 가장 적합한 W를 찾는 방법도 있을 수 있다. 근데 그렇게 할거면 차라리 안하는게 낫다. 그래서 이 강의에서 알려주는 방법이 'follow the slope' 라는 방법이다. 경사를 따라가라는 뜻이다. 바꿔말하면 초기 W 벡터에서, 미분을 이용해 최적의 W를 찾는 법을 이야기하는 것이다.

위 사진은 1차원에서의 미분을 나타내는 식이다. 그러나 우리는 이 개념을 다차원을 가진 W 벡터에 적용해야 한다. 다차원에서는 이를 gradient라고 한다. gradient는 벡터의 각 차원의 편미분값들을 모아놓은 벡터이다. 만약특정 차원에서의 기울기를 알고 싶다면, gradient 벡터와 그 차원을 나타내는 unit vector를 dot product를 해주면 된다. 어쨌든 이 방법의 요점은 각 차원에서의 기울기를 봐서 가장 가파른 곳으로 이동하며 최적화를 진행한다는 점이다. 이를 계산하는 방법에는 두 가지가 있다.
1. Numerical gradient

이렇게, 첫번째 차원부터 0.0001이라는 작은 숫자를 더해 loss가 어떻게 바뀌는지 보고, 그때의 dW를 계산한다. 여기서 0.0001은 위의 1차원 미분에서의 h와 같다. 이 자체도 하이퍼 파라미터다. 그런데 이렇게 모든 차원을 계산하는 것은 시간과 비용이 너무 많이 든다. 따라서 우리는 두 번째 방법을 더 선호하고, 많이 사용한다.
2. Analytic gradient
두 번째 방법은 미분을 이용해 계산해 나가는 방법이다. 첫 번째 방법보다 훨씬 빠르고 정확하다. 그러나 알아야할 것은 첫 번째 방법은 검산할 때 사용한다는 것이다. 이를 gradient check이라고 하는데, analytic gradient를 구해서 이를 검산할 때 numerical gradient를 사용한다는 것이다.
3. Gradient Descent

이것이 앞에서 말한 slope가 낮아지는 방향으로 파라미터들을 업데이트 시키는 방법이다. 그러나 데이터의 양이 많아진다면 이렇게 모든 데이터에 대해 할 수 없을 것이다. 그래서 나온 방법이 SGD이다.
4. Stochastic Gradient Descent(SGD)
이 방법은 데이터가 너무 많으니 반복문을 돌 때마다 mini batch를 뽑아서 이를 이 mini batch를 기준으로 파라미터를 업데이트하는 것이다. 이렇게 하면 시간과 비용이 많이 절약될 수 있다.
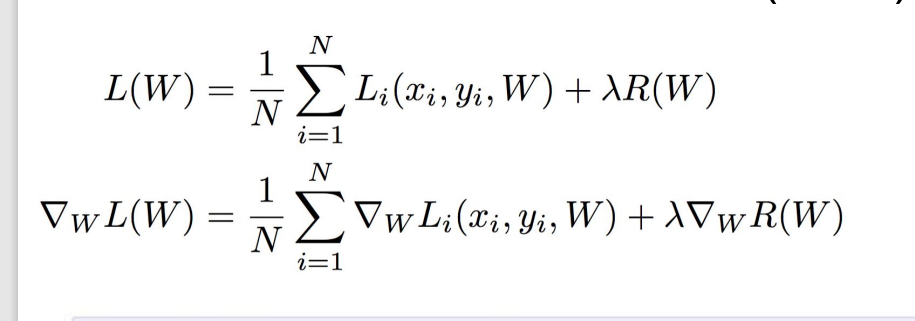
8.결론
아직 코딩을 해보지 못해 실제 코딩을 할때 지금까지 배운 원리들이 어떻게 적용되는지는 모르겠다. Assignmetnt1을 이제 슬슬 건드려볼 때가 온 것 같다. 다음 강의부터는 본격적으로 Neural network에 들어가게 된다.
