1. 3강 복습
지난 번 강의에서는 Softmax function과 SVM을 배웠고, Regularization을 배웠다. 그리고 테스트 데이터를 가장 잘 설명하기 위한 gradient를 찾기 위한 방법으로 gradient descent를 배웠다. 데이터의 크기가 너무 크다면 Strochastic gradient descent를 이용해 mini batch를 뽑아 최적화를 진행하기도 했다. 그렇다면 이제 실제로 어떻게 analytic gradient를 계산하고, 업데이트 하는지 살펴보자.
2. Computational Graph
gradient를 업데이트하는 과정 중에 가장 첫 번째로 해야 하는 과정이다. 쉽게 말하면, f=Wx라는 식뿐만 아니라, 임의의 복잡한 식이 들어오더라도 gradient를 쉽게 계산할 수 있게 해주는 방법이다. 모든 식에 적용할 수 있다는 것이 이 방법의 가장 큰 장점이다. 디지털 시스템에서 gate들을 표현했던 것과 비슷한 것도 같다. 뒤에서 하겠지만, computational graph로 식을 표현한 뒤, back propagation이라는 것을 사용해 새로운 gradient를 찾아내는 것이다.
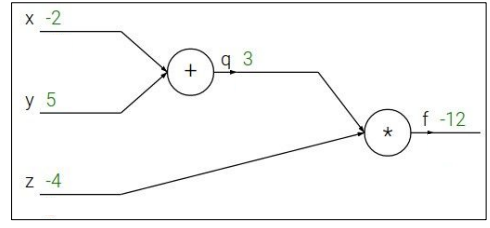
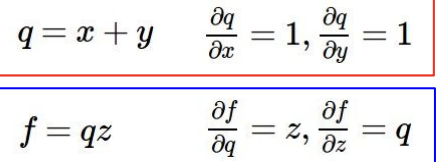
위의 첫 번째 사진이 f에 대한 computational graph이다. 초록색 숫자들은 그냥 예시를 위해 써놓은 이다. (정확히는 값을 정하고, 그들을 이용해 값을 계산한 것이다.) 여기서 등장하는 개념이 편미분인데, 간단히 생각하면 여러 변수를 가진 식 중에 내가 관심 있는 하나의 변수에 대한 미분값에만 집중해서 보는 것이다. 그 변수 이외에는 다 상수 취급하면 된다. 여기서 사용되는 또 다른 개념은 chain rule이다. 편미분 값을 여러개 이용해 원하는 편미분 값을 찾아내는 것이다. 이제 local gradient와 global gradient의 개념만 배우면, gradient 업데이트를 하기 위한 준비는 끝난다.
- local gradient: 주어진 값들로 미리 구할 수 있는 gradient를 의미한다. forward pass를 할 때 구해진다.
- global gradient: backward pass때 구하는 것으로, 새로운 gradient를 업데이트할 수 있게 해준다.
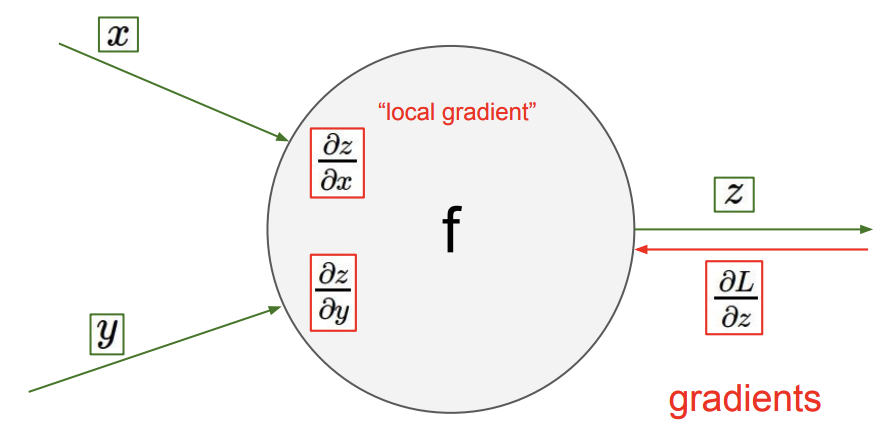
local gradient를 구할 때는 미리 주어진 값과 그들의 관계식을 이용한다.
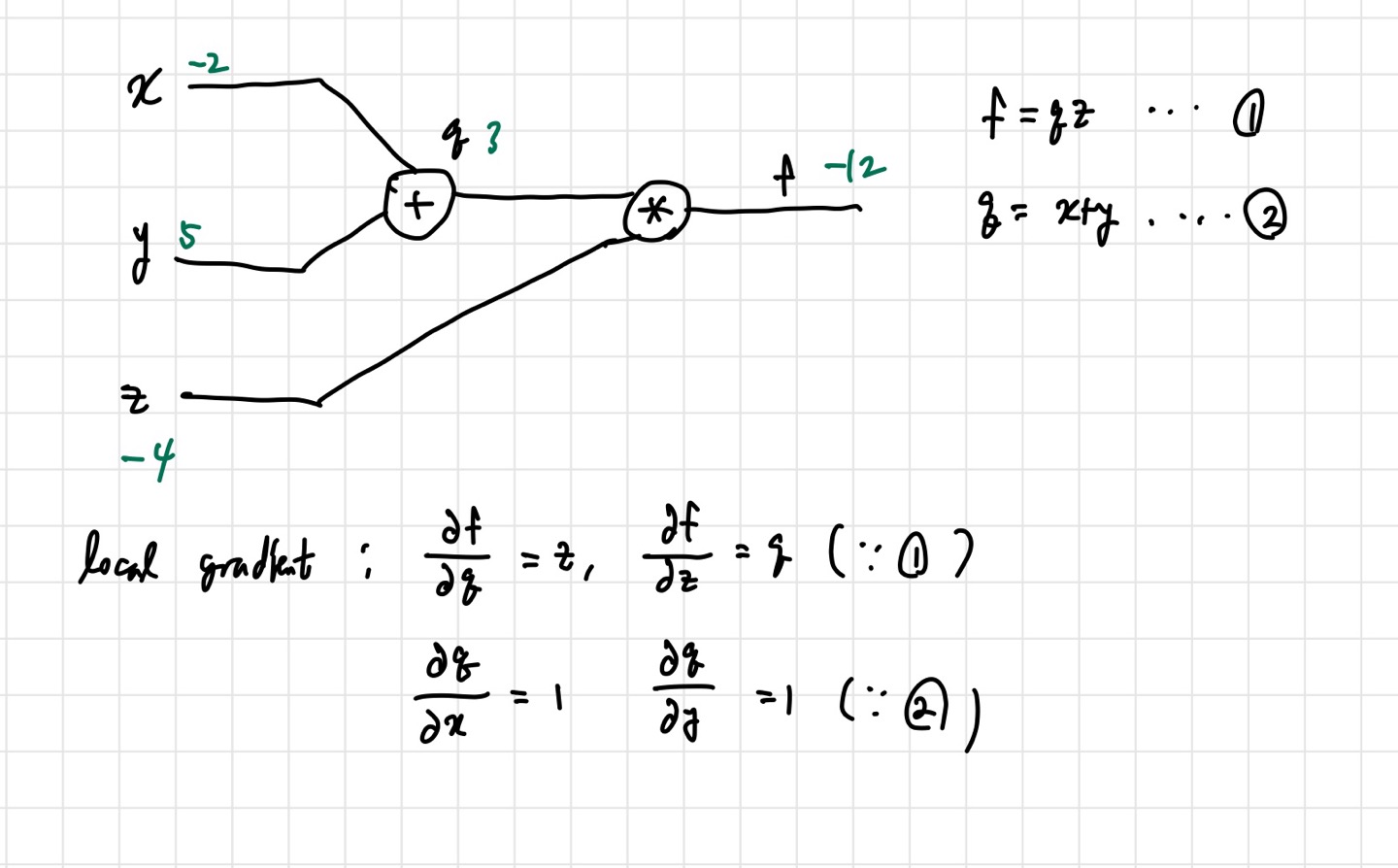
위의 필기가 우리가 얻을 수 있는 local gradient들을 계산한 것이다. 이제 global gradient를 이용해 뒤에서부터 gradient들을 최적화해 나가는 것이다.
3. Backpropagation
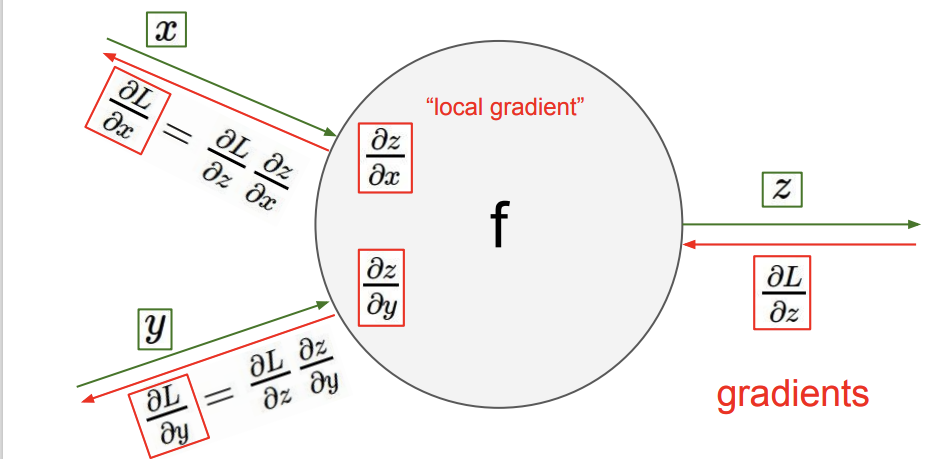
뒤에서 global gradient 가 들어오면, 이를 통해 의 gradient를 업데이트한다. 이 과정을 back propagation이라고 한다. 이걸 계산하는 나름의 공식을 써보자면 updated gradient= local gradient * global gradient 가 된다. 이제 공식도 알았으니, 예시에 적용해보자.
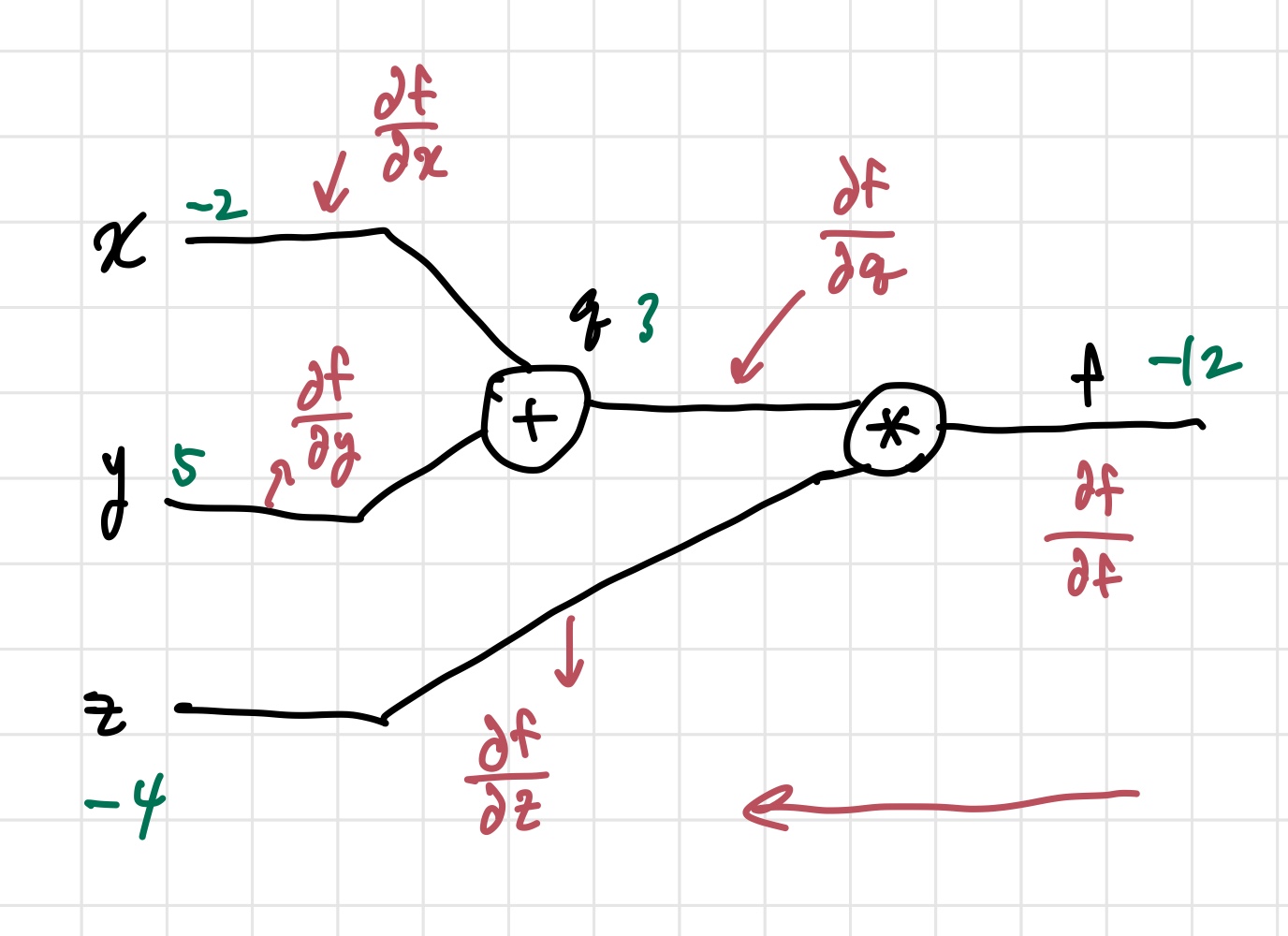
빨간색으로 써놓은 것이 각 선이 나타내는 gradient 값이다. 우리가 알고 싶은건 각각의 input 가 최종 output인 에 얼마나 큰 영향을 미치는지이다. 식으로 보면, , , 이다. 위 필기로 보면, backpropagation을 끝까지 하고 나면 저 값들을 알 수 있다. 앞에서 말했던 chain rule이 여기서 사용된다. 빼고는 바로 구하지 못한다. 그렇기 때문에 두 개의 편미분 값으로 분리해서 chain rule을 적용해 구하는 것이다.
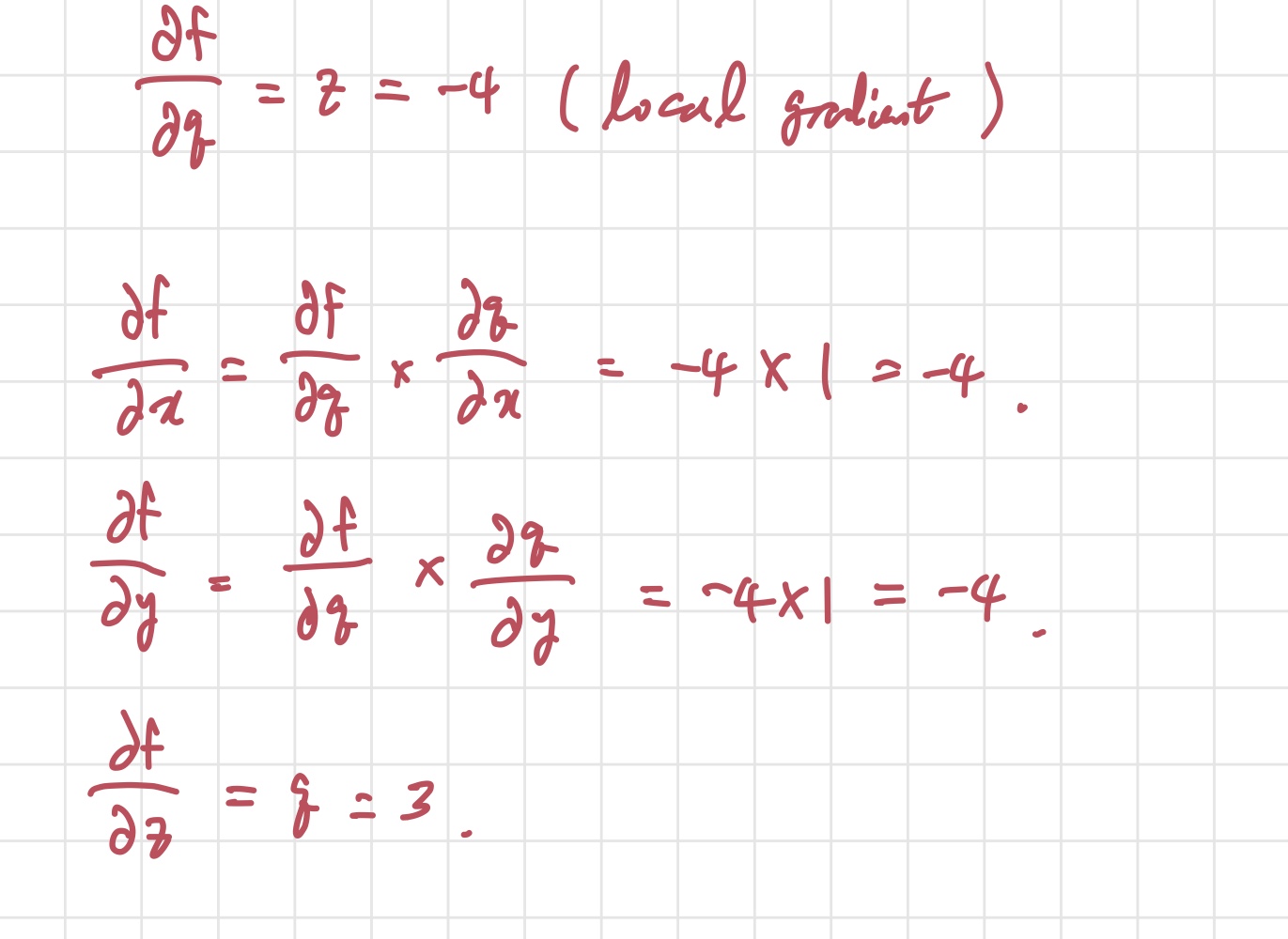
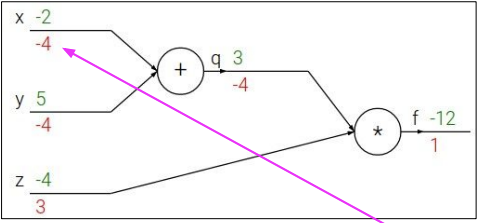
이렇게 우리가 알고 있는 값들을 통해 gradient 업데이트를 진행한다. 그런데, 실제 우리가 직면하는 문제들은 방금 본 것처럼 예쁘게 주어지지 않는다. 그렇기 때문에, 더 복잡한 식이 주어졌을 때의 예시를 보자.
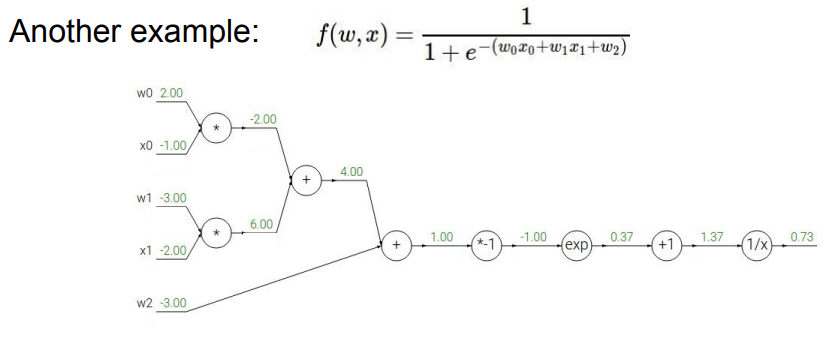
이렇게 식이 주어지고, computational graph를 그린다. 그리고 앞에서와 같이, 맨 뒤에서부터 back propagation을 적용해보자. 식이 길어서 노드 하나씩 끊어서 볼 것인데, 각 노드에 적혀있는 식을 라고 취급하자.
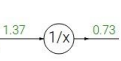
일단, 로 놓고 문제를 살펴본다. 위에서와 마찬가지로, 맨 뒤의 값은 1로 설정하고 시작한다.

저렇게 놓고 위에서 한 것과 동일하게 진행하면, 업데이트된 -0.53이라는 gradient가 나온다. 이 gradient는 다음 노드의 global gradient로 사용된다.

다음 노드도 마찬가지로 진행하면 된다. 주의해야할 것은, +1만 써있다고 로 놓으면 안된다는 것이다. 들어오는 input x에 1을 더하는 것이기 때문에 로 놓아야 한다. 이후 다른 노드들에서도 똑같은 작업을 해주면 된다.
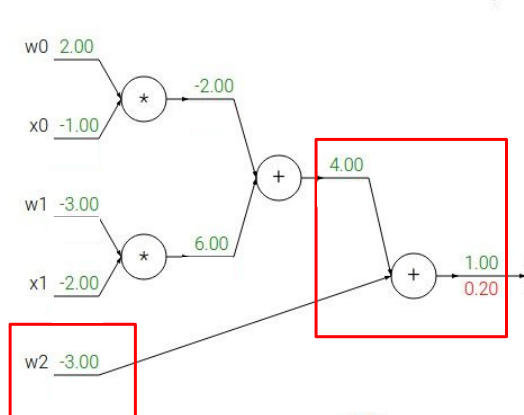
그런데 이 과정을 계속하다 보면 addition node를 만나게 된다. 딱히 어려울 것은 없다. 원래 하던대로 하면 되는데, addition gate의 경우 local gradient의 값이 항상 1이다. 왜 그런지는 직접 해보면 알 수 있다. 아래 사진은 내가 임의로 그린 computational graph이다.
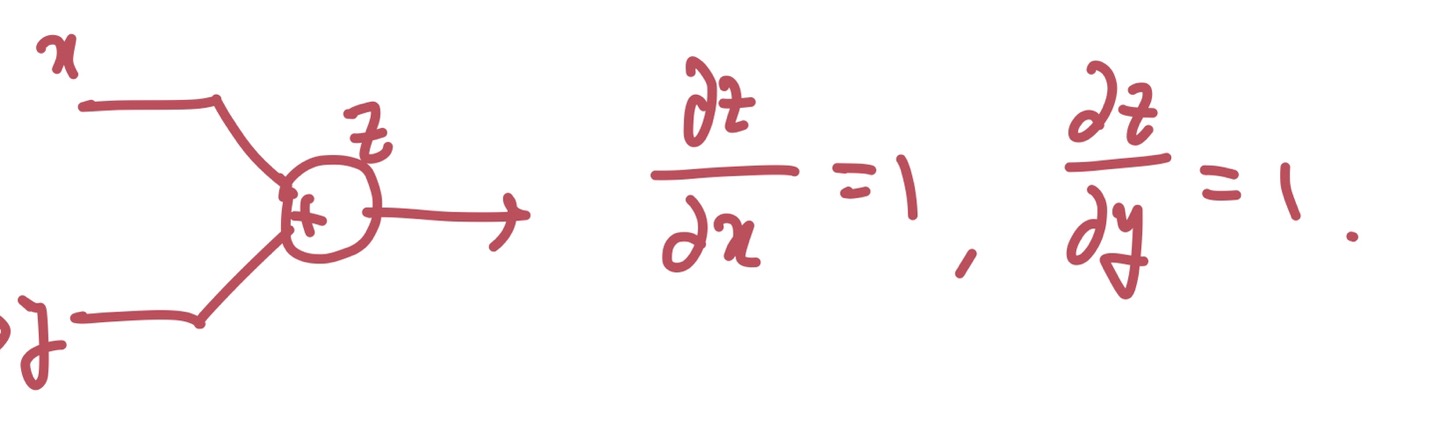
그림을 좀 못 그리긴 했지만, 어떤 문자로 z를 편미분하던 간에 local gradient는 1이 나온다. 이렇게 써놓고 보면 당연한 얘기다.
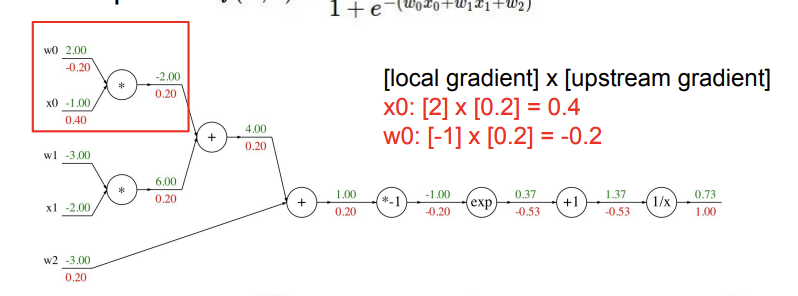
multiplication node를 만났을 때는 어떨까? 위의 사진을 보면, w0는 x0 input을 local gradient로, x0는 w0 input 값을 local gradient로 갖게 된다. 이것도 내가 addition gate에서 한 것처럼 간단한 computational graph를 그리고 직접 편미분을 해보면 알 수 있다.
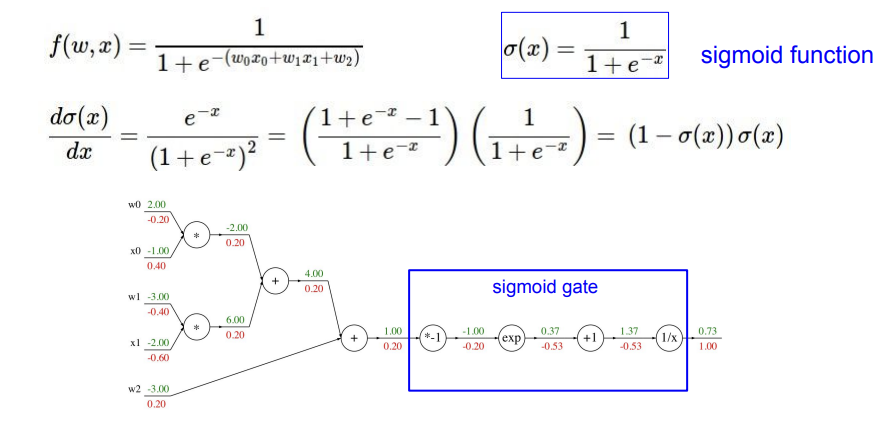
어쨌든 이런 과정들을 반복하다 보면 updated gradient가 구해지게 된다. 그런데 여기서 중요한 지점들이 몇가지 있다. 지금은 computational graph를 모든 연산을 하나의 노드에 배정해 그렸지만, 꼭 그렇게 해야하는 것만은 아니다. local gradient를 구할 수만 있는 식이라면, 여러 노드들을 합쳐서 하나의 노드로 만들어도 된다, 우리가 많이 사용하는 sigmoid function의 형태를 띄고 있으니, sigmoid function으로 하나의 노드를 만들어보자.
4개의 노드를 하나의 sigmoid gate로 합쳐도 문제가 없다. sigmoid function을 이용해 gradient를 구해도 똑같이 나오는 것을 알 수 있다.
또 하나 눈여겨 봐야 할 것은 gate별로 고유한 특성을 가진다는 것이다.
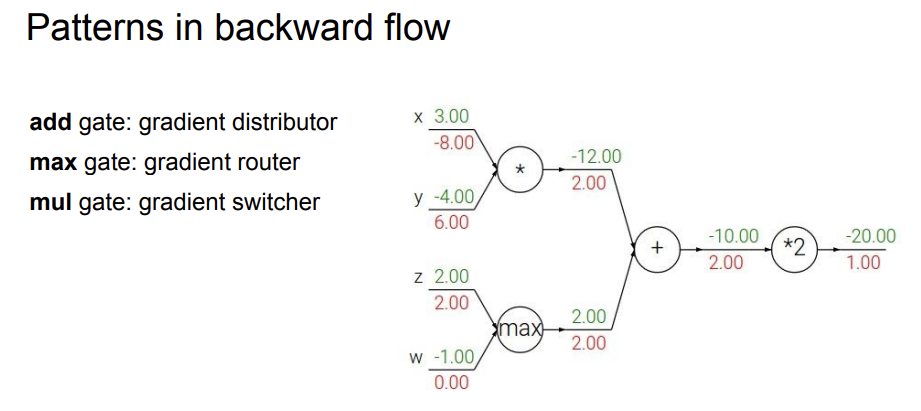
- add gate: gradient를 나눠주는 효과가 있다. 두 개의 branch에 global gradient가 그대로 들어간다.
- max gate: gradient router라고 하며, 두 개의 branch 중 하나의 branch에 값을 주고, 나머지에는 0을 할당한다. (max 값만 의미가 있기 때문에, 나머지는 0을 할당하는 것이다.)
추가로 설명하자면, max gate는 backprop시 가장 큰 input을 갖던 branch에게 gradient distribution을 진행하며, 이게 가능한 이유는 그 branch에만 1의 gradient를 주고, 나머지 branch들에게는 0을 주기 때문이다. - mul gate: gradient switcher라고 하며, 하나의 branch의 gradient를 구할 때 다른 branch의 input을 이용해 구하게 된다. (앞의 식의 편미분값들을 보면 이해가 편하다)
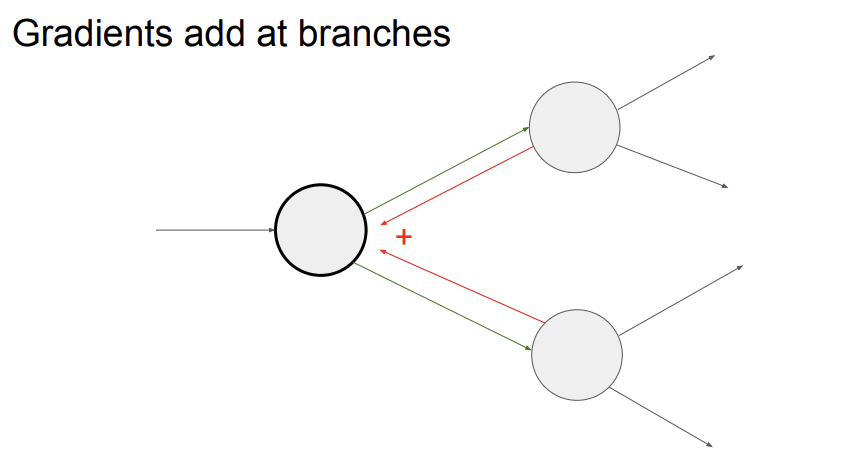
그리고 마지막으로, global gradient 여러 개가 하나의 노드로 들어온다면, 들어온 global gradient들을 다 더해서 생각하면 된다.
4. Gradients for vectorized code(Jacobian matrix)
위에서는 input들이 모두 하나의 변수였다. 그러나 딥러닝에서는 input들이 벡터로 들어오는 경우가 더 많다. 벡터가 input으로 들어오는 경우 Jacobian matrix라는 것을 알아야 한다. Jacobian matrix는 편미분 값들이 담긴 행렬이다.
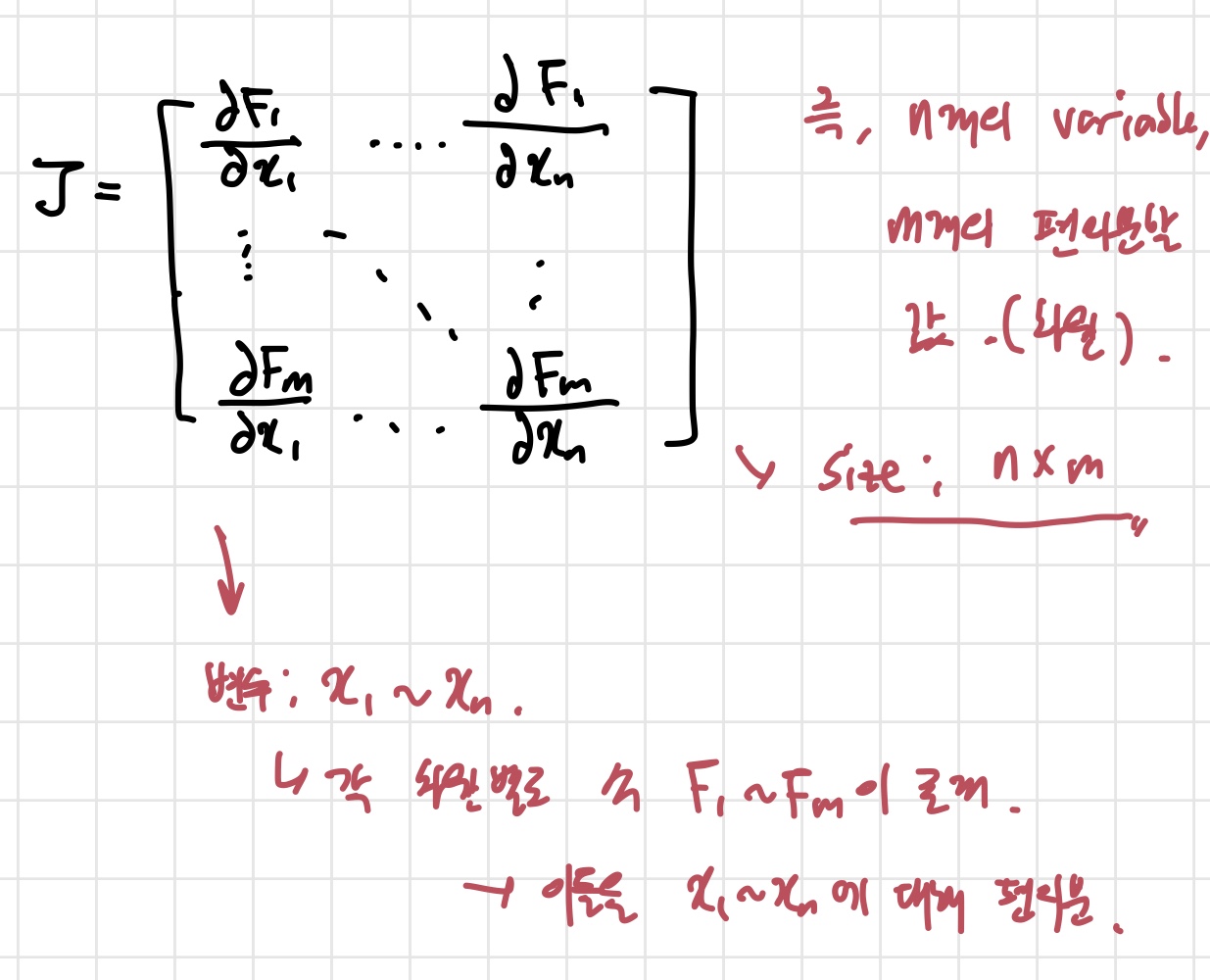
다변수 미적분학을 공부한게 아니라, 이해하는데 애를 먹었다. 간단히 정리하자면, 각 차원에 F라는 식들이 존재할텐데, 이 F는 n개의 변수를 갖는다. 따라서 F를 n개의 변수에 따라 편미분한 값들이 하나의 행에 쭉 나열되는 것이다. 그 다음 행에는 또 다른 input에 대한 편미분 값들이 있는 것이다.
이렇게 갑자기 Jacobian matrix를 한 이유는 벡터가 input인 경우 update gradient가 Jacobian matrix 형태를 띄기 때문이다.

나도 정확하게 감은 안 오지만 그냥 그렇구나,,, 하고 넘어간다. 예시를 하나 들어보면,
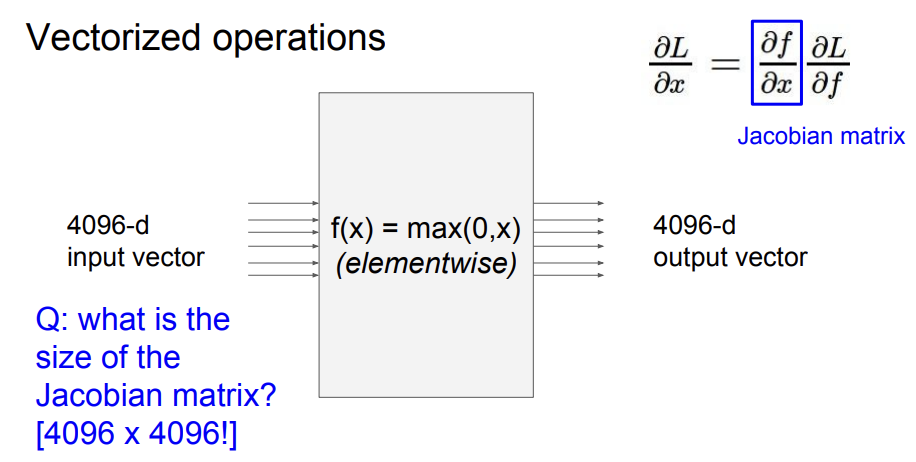
max 함수인 에 통과시킬 때, 가 Jacobian matrix가 된다. 이 경우, Jacobian matrix는 대각 행렬이 된다. 실제로 이걸 다 계산하긴 쉽지 않고, 그냥 gradient만 구해서 넣는다고 한다.
5. Vectorized example
내가 4강에서 이해하는데 가장 애먹은 부분이다. 행렬 크기 생각하고 식도 해석하다 보니 오래 걸렸다.

이전과 다른점은 역시 input이 모두 벡터, 행렬이라는 점이다. 전과 같이 숫자 계산하는 것이다. 아 그리고 계산되는 gradient들도 당연히 다 벡터로 나오는데, 그 크기는 input vector와 같아야 한다. 이제 backprop를 진행해보자. 는 이번에도 1로 놓고 시작한다.
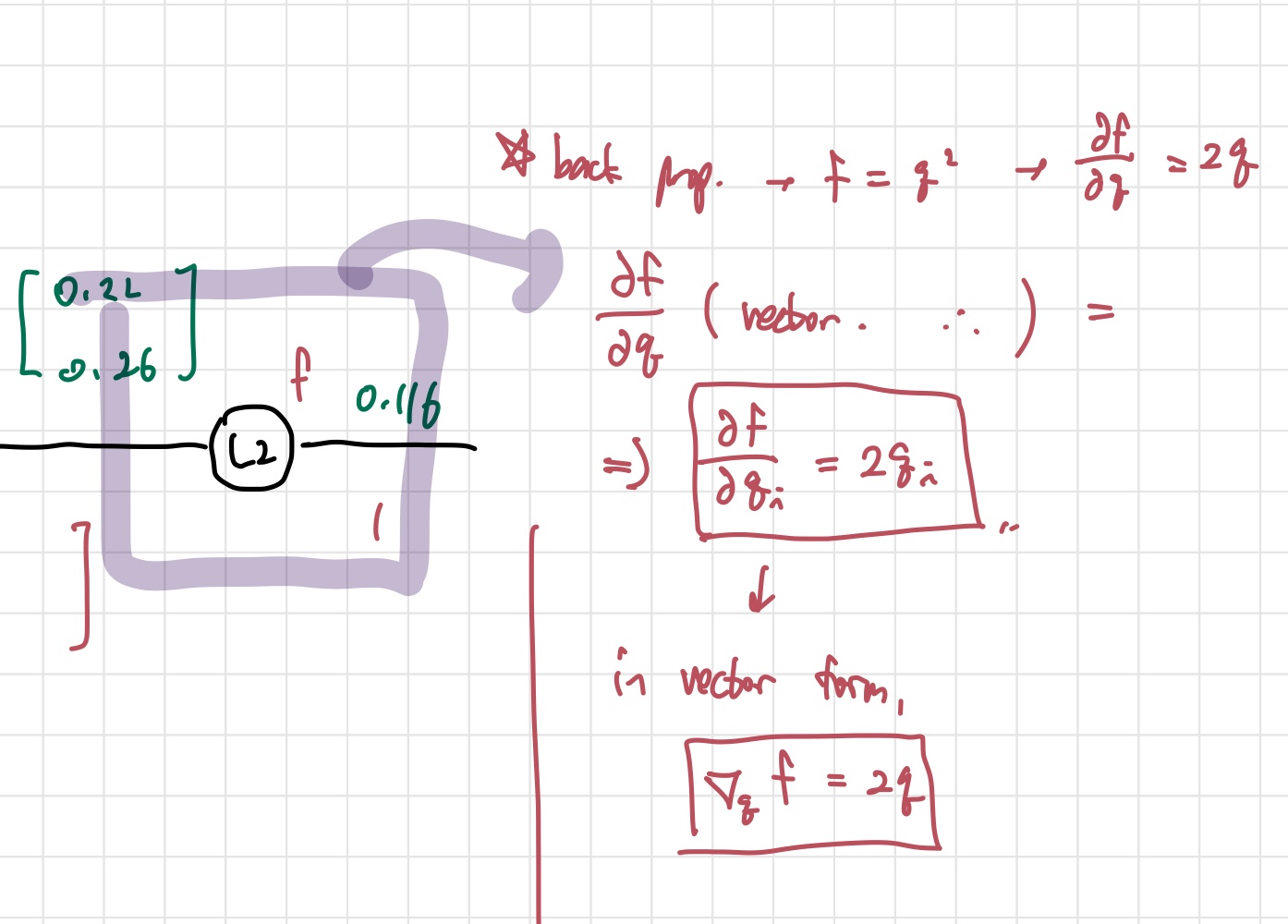
벡터에서 다른 점은, 벡터 안에 여러 개의 원소들이 있으니까, 그 요소들의 미분값을 따로 계산해줘야 한다는 것이다. 이 사진 위의 사진을 보면 는 L2를 사용하기 때문에 벡터의 원소들을 다 제곱해서 더한 형태를 띈다. 이때 벡터의 원소를 각각 분리해서 본다면, 라는 값을 얻게 된다. 는 벡터에서 우리가 어떤 원소를 사용하고 있는지 알려주기 위함이다. 위 과정을 마치면 의 gradient 값을 구할 수 있게 된다. (는 mul gate의 intermediate variable이다.)
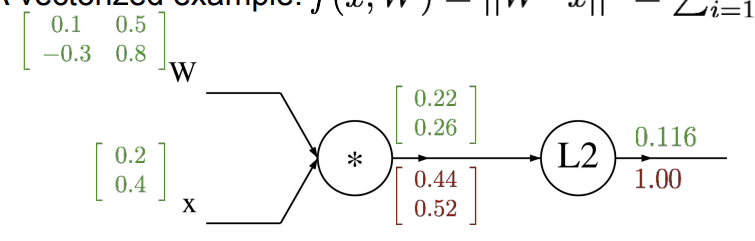
의 각 원소에 2배를 해준 것이 local gradient가 되기 때문에, 0.44, 0.52를 얻게 되는 것이다. 이제 W로 가보자.
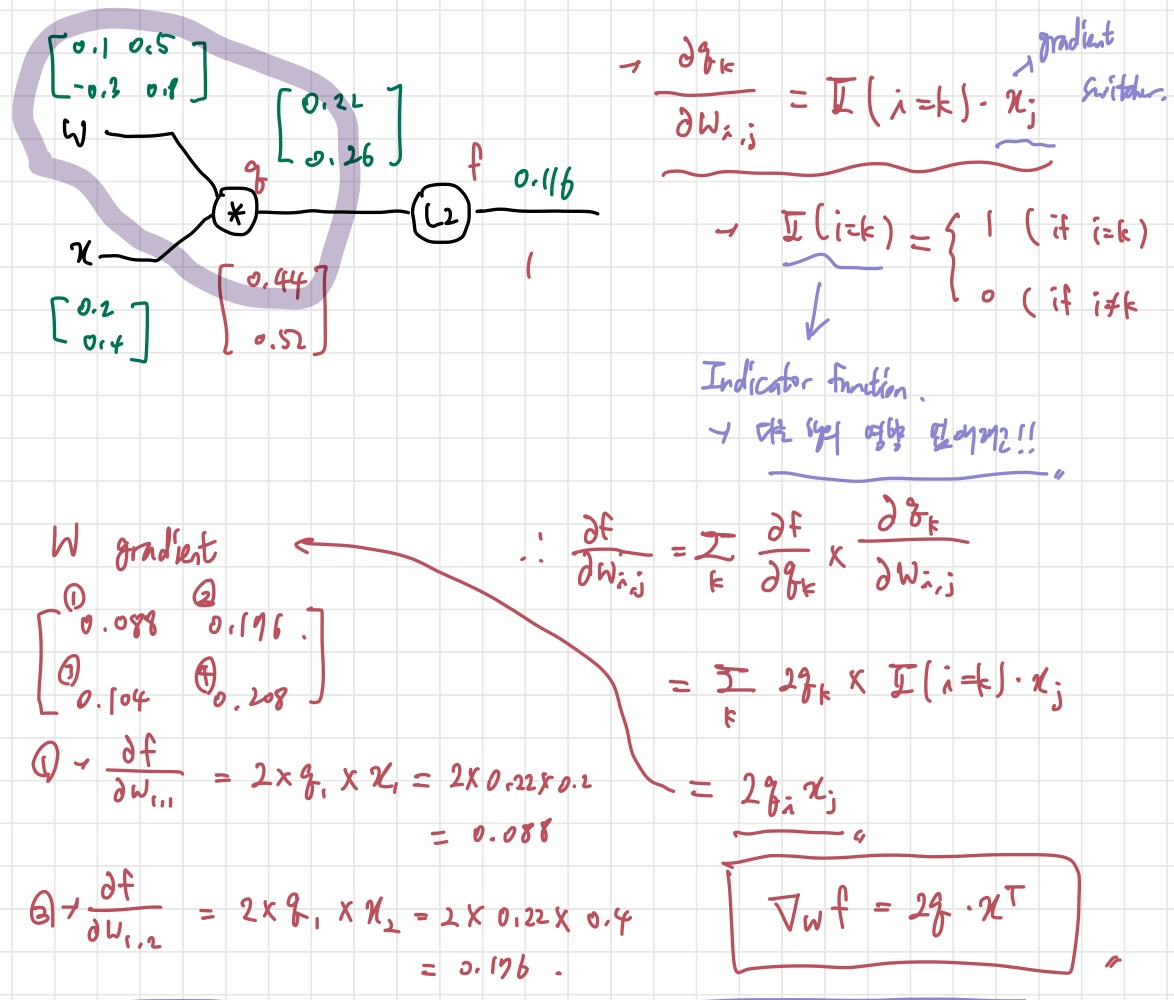
어려워 보이지만, 차근차근 이해하면 된다. 먼저, 를 구해보자. 앞서 mul gate는 gradient switcher의 역할을 한다고 배웠다. 그렇기 때문에 반대쪽 branch의 input인 가 답이 된다. 단, 여기서 와 의 벡터 크기가 같지 않기 때문에, 다른 행의 영향을 없애고 같은 행의 영향만 고려하고자 Indicator function을 붙인다. 여기서 끝이 아니고, 우리가 구해야 하는 것은 이기 때문에 chain rule을 이용해 계산해주면, 마지막의 가 나오게 된다. 이것이 최종 식인 것이다.
이제 마지막으로 를 구해보자.
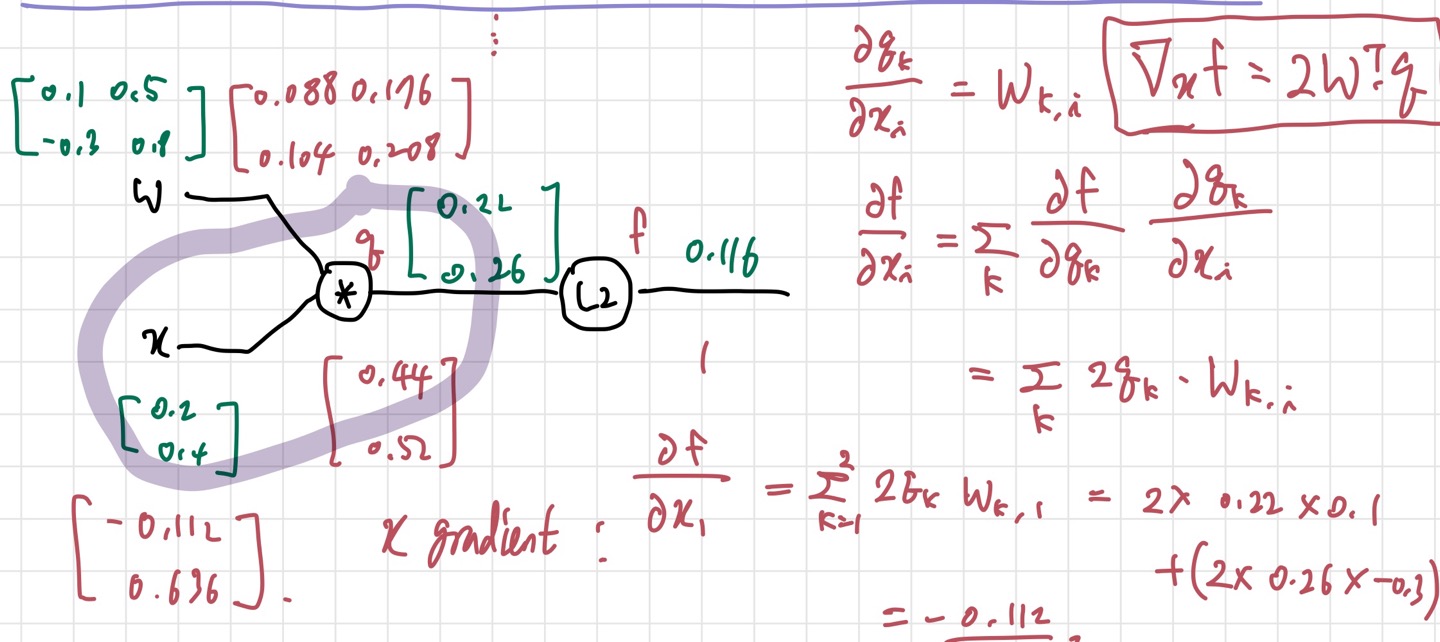
마찬가지로, 먼저 구하면, gradient swicher에 의해 가 나온다. 그리고 chain rule을 적용해 를 구하면 된다. 실제 코딩을 할 때는 forward pass 함수, backward pass 함수, 그리고 각각의 gate들을 함수로 만들어서 사용한다고 한다. 코딩은 해봐야 감이 좀 올 것 같고, 아직은 실감이 잘 나지 않는다.
6. Neural Network
드디어 Neural Network 까지 왔다. Neural Network 를 구성하는 기본 요소는 Linear Classifier이다. 단지 Neural Network는 이를 여러 겹 쌓아서 만든 것이다. 더 정확하게 사물들을 분류할 수 있게 해주는 효과가 있다. 그러나, 각 layer 사이에는 non linear function이 껴 있어야 한다. linear하다면 output 또한 linear function이 나오므로, 더 복잡한 것을 분류하기 위한 우리의 취지와는 전혀 맞지 않기 때문이다.
일단 2-layer neural network만 살펴보자.
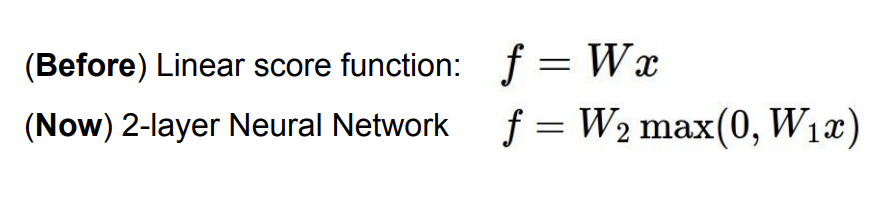
식은 이렇게 나타낼 수 있다. 굳이 구조도를 그려보자면 이렇게 된다.

이전에 배운 linear classifier는 h라는 요소가 없없다. 따라서 하나의 벡터가 각 class당 하나의 template만 만들 수 있었다. 만약 말을 분류해야 하는데 input image가 왼쪽을 보고 있는 말, 오른쪽을 보고 있는 말이 있다고 하자. 우리는 하나의 template만 정할 수 있으므로, training data로 모델을 훈련할 때 왼쪽과 오른쪽 말 중 하나만 골라 template으로 만들 수 있다. 이렇게 되면 말이 내 template과 다른 쪽을 보고 있다면 정확도가 현저히 떨어지게 된다.
그러나 지금 배우는 Neural network는 이 문제를 해결해 여러 개의 template을 가질 수 있게 해준다. 이제 가 무엇을 의미하는지 알아보자.
1. : 여러 template들이 겹쳐진 weight vector
2. : 를 에 넣어서 나온, 각 template을 얼마나 사용해야 하는지에 대한 score vector
3. : 에 맞춰 weighting을 해서 final score인 를 얻는다.
3-layer neural network 도 비슷한 형태를 가진다.
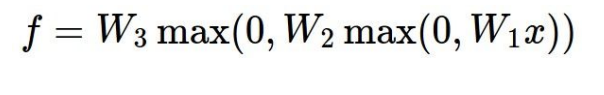
이런 식으로 계속 layer가 증가할수록 많이 겹쳐지는 형태이다.

Neural Network의 구조는 이렇게 된다. Fully Connected 구조라고 하며, 화살표로 보다시피 모든 구성 요소들이 서로 연결되어 있어 붙여진 이름같다.
본격적인 내용 들어오니까 어렵다..빨리 실습이라도 해봐야 이해가 될 것 같다.
