cs231n 5강

1. 4강 복습

  4강은 양이 꽤 많았다. 주요한 주제들만 짚고 넘어가자. 먼저 back propagation을 이용해 computational graph를 다루는 것에 대해 배웠다. 이는 임의의 식에 대해 일관된 방법으로 계산이 가능하다는 점에서 의미가 있었다. 그리고 back propagation을 통해 gradient를 계속 업데이트 할 수 있었다. 우리가 주로 접하는 input 값은 벡터이므로, 이러한 방식을 벡터에 적용해 Jacobian matrix가 등장하기도 했다. 그리고 나서 2-layer Neural Network에 대해 간단히 배웠는데, 이는 Linear classifier를 2개 겹쳐놓은 것이었다. 그러나 두개의 layer 사이에 nonlinear 식을 두어 output이 그냥 하나의 linear한 식이 나오지 않게 하였다. 이를 통해 전에는 클래스 별로 하나씩만 만들 수 있었던 템플릿을 여러개 만들 수 있게 되었다.

2.Convolutional Neural Network

  이번 강의에서 배울 가장 중요한 개념이 CNN이다. 아직 다 배우지 않아서 모르겠지만, 내가 배우는 분야에서 필수적인 개념이라고 한다. 줄여서 ConvNet이라고 하고, classification, retrieval(이미지 검색), detection, segmentation, pose recognition등 쓰이는 곳이 너무나 많다. 이전에 4강에서 배운 2-layer Neural Network는 Fully Connected Layer 이다.

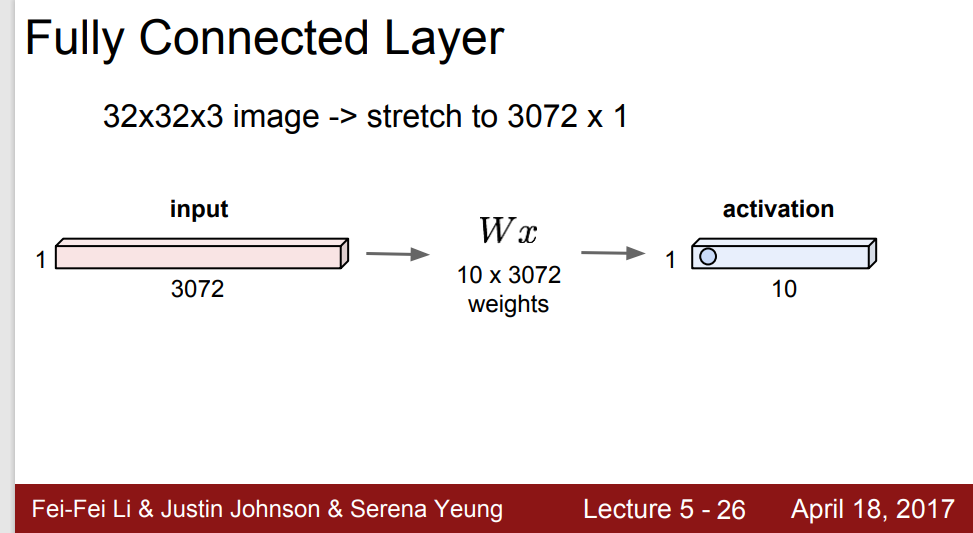
  일단 input을 쭉 늘어놓은 다음, weight 벡터를 곱하고, 이를 토대로 output이 오는 방식인 것이다. 그런데 지금 배울 ConvNet은 이렇게 쭉 늘려서 input을 만들지 않는다. Spacial structure를 건들지 않고 output을 얻는다는 뜻이다.

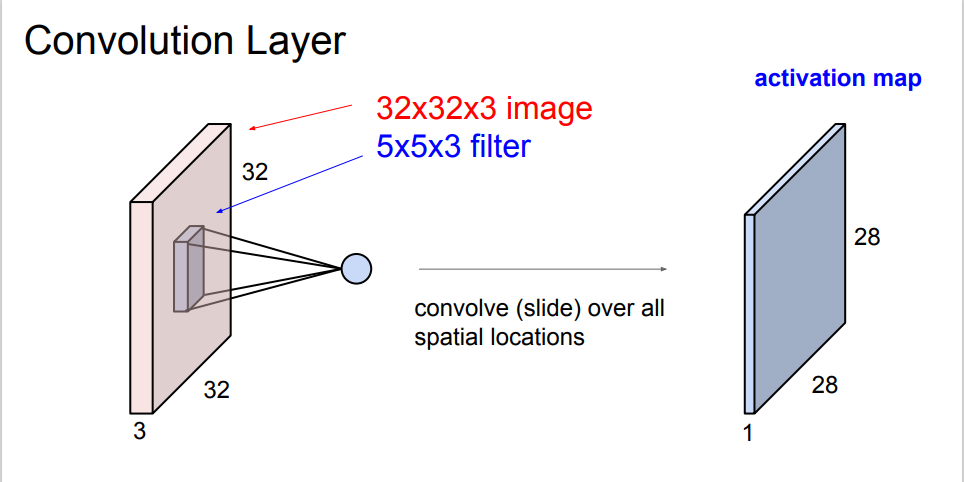
  이렇게 input의 형태를 유지하며 임의로 만든 filter가 공간을 다 돌아다닌다. 그렇게 함으로써 output이 나오는 것이다. 그런데 이때 주의해야 할 점은 filter의 depth와 input의 depth는 같아야 한다는 것이다. 또한, filter를 여러개 씌울 수 있는데, 이렇게 되면 filter를 씌우는 순서 또한 중요해진다. 이때 output의 depth는 씌운 filter의 개수와 같다. 위의 그림에서는 하나의 filter만 사용했으므로 output의 depth가 1이다. 만약 6개의 filter를 사용했다면, 아래의 그림처럼 나올 것이다.

output의 height와 width가 28인 이유는 filter가 가장자리의 픽셀까지는 닿지 못하기 때문이다.   지금까지 본건 Convolution Layer 한 개이다. 앞서 말한 ConvNet은 이 Convolutional Layer가 여러개 연속해서 쌓인 형태이다. 그리고 위의 사진에서 activation map 이라는 개념이 등장하는데, 이는 인공 신경망에서 비선형성을 대입하기 위해 만든 식이다. 하나의 filter는 하나의 activation map을 준다. 이를 통해 무엇을 활성화시키고, 무엇을 활성화시키지 않을지 결정하게 된다. 실제로 쓸 때는 Conv-> RELU->Conv->ReLU->pool이 반복되어 나타난다. (여기서 ReLU는 다른 식으로 바꿀 수 있다.) pool은 activation map의 크기를 downsampling 해주는 것인데, downsampling하는 속도가 너무 빨라도, 너무 느려도 좋지 않다고 한다. 이 과정을 그림으로 보면 이렇다.

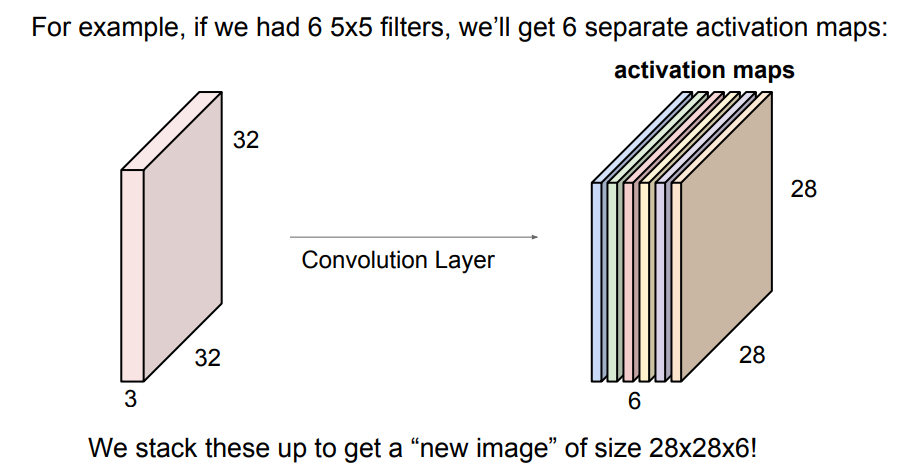
마지막으로, 넘어가기 전에 가장 중요한 2개를 정리하자.

1. filter 개수 = activation map의 개수이다.
2. filter depth = input depth 여야 한다.

3. Spacial Dimension

  이제 앞에서 말한 filter가 어떻게 input을 돌며 계산을 하는지 살펴보자.

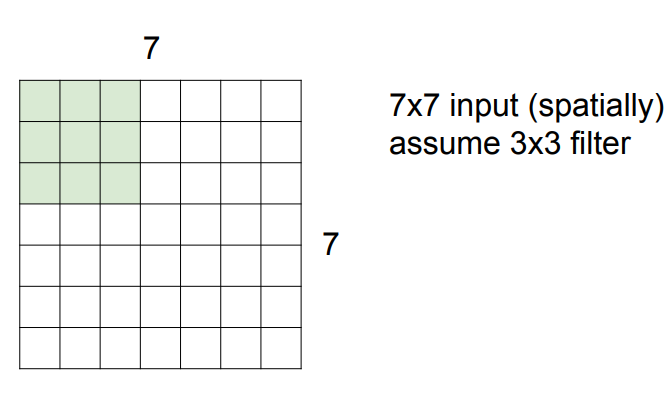
input이 $7*7$이라고 가정하고, $3*3$ filter가 돌고 있다고 가정하자. 필터 범위 내에 있는 9개의 값을 이용해 필터 기준 가운데 픽셀 값을 예측하는 것이다. 그렇기 때문에 가장자리 픽셀들은 돌지 못한다. 그 옆에 픽셀들이 존재하지 않기 때문이다. 필터는 왼쪽 위에서 시작해서 오른쪽 밑까지 차례대로 훑는다. 그러면 output은 $5*5$가 된다.
 방금은 필터가 뛰어넘은 픽셀들이 없다고 가정하고 output을 뽑았는데, 실제로는 픽셀들을 뛰어넘으며 output을 얻을 수도 있다.

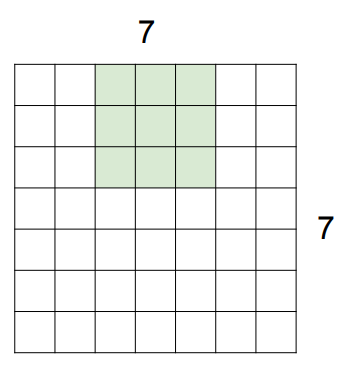
  위의 사진들과 같이, 하나의 픽셀을 뛰어넘고 가면, stride=2라고 표현한다. 즉, stride에 따라 뛰어넘는 픽셀 개수가 달라지는 것이다. 그렇다면 stride가 3이라면 어떨까? 이 경우는 필터가 딱 맞아떨어지게 돌 수 없으므로 쓰지 않는다.
 이렇게 해서 공식을 통해 output size를 일반화할 수 있는데, 그 공식은 아래와 같다.

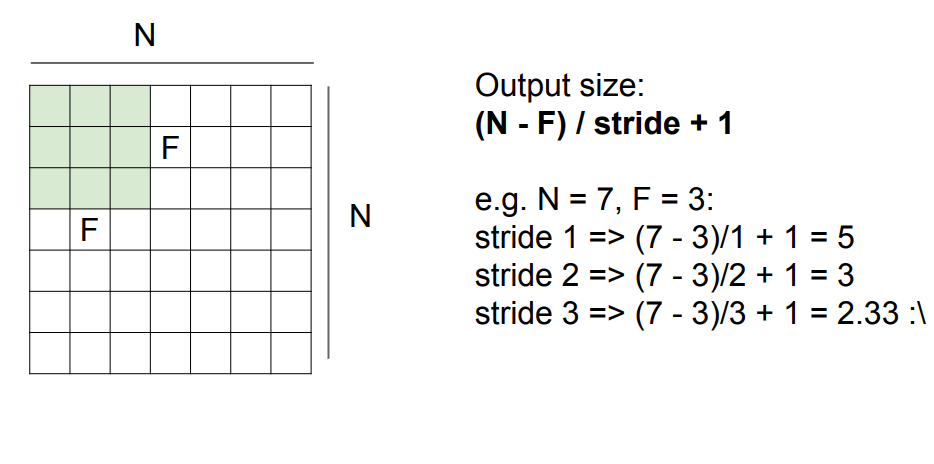
  그리고 실제로는 가장자리에 픽셀을 둘러 필터가 딱 맞게 돌 수 있도록 input을 변형시키기도 한다. 만약 $7*7$ input에 가장자리를 0로 padding하고 stride를 1로 설정했다면, input은 $9*9$가 될 것이다. 이것을 공식에 넣어보면, $O ={(9-3)\over 1} + 1=7$ 이므로 $7*7$이 output size가 된다. depth가 존재한다면, output=$7*7*$(사용한 필터 개수) 가 되는 것이다. 공식을 정확히 정리하고 넘어가자.

O= ${N+2*P-D*(K-1)-1\over S}+1$
N: Image size, P:padding, D:dilation, K:kernel size, S: stride를 뜻한다.

  그런데, 중요한 점은 layer를 하나 거칠때마다 output의 크기가 줄어든다는 것이다. 이때 너무 빨리 줄어드는 것은 좋지 않다. 예시를 살펴보며 확실히 이해하자.

  위와 같은 문제가 있다면, 공식에 의해 output은 ${(32+2*2-5)\over 1}+1=32$이다. 그런데 filter가 10개 였으므로 최종 답은 $32*32*10$이다. 이렇게 padding을 조절함에 따라 output volume의 사이즈를 보존할 수도 있는 것이다.
 이번엔 parameter에 관한 문제이다.

  위와 같은 문제가 있다고 하자. 이때는 filter만 신경쓰면 된다. 하나의 필터에서 $5*5*3+1=76$이 나오고, filter가 10개 있으므로 $76*10=760$개의 parameter가 나온다. 1을 더해주는 이유는 bias 때문이다. 보정효과를 주는 것 정도로 생각하면 될 것 같다. 일반적으로 코딩을 하며 사용할 때, 아래 사진과 같이 설정하고 사용한다.

K: 필터 개수, F: 필터 크기, S: stride, P: zero padding 개수

4. Pooling Layers

  앞에서도 Pooling에 대해 잠깐 언급했다. Pooling을 하는 목적은 우리가 다루기 편하게 하려는 데에 있다. 이때 depth는 건들지 않는다. 여러 가지 pooling 방법들이 있지만, 제일 대표적인 건 max pooling이다.

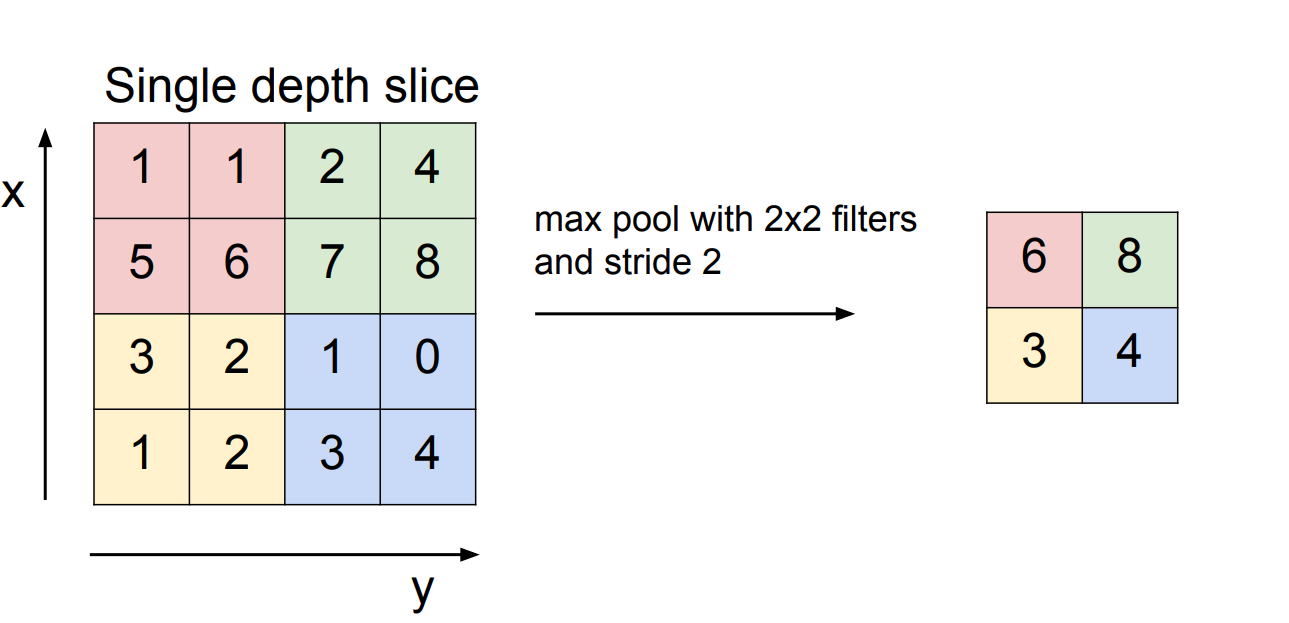
이렇게 필터를 정하고, 각 필터의 최댓값인 것만 뽑는 것이다. 물론 필터 사이즈와 stride는 바뀔 수 있다. 가장 많이 사용하는 조합은 $F=2, S=2$ 혹은 $F=3, S=2$ 이다. pooling을 할 때에는 stride를 필터간에 overloop이 없게 설정하는 것이라고 한다.