이 글은 과제를 하면서 내가 막혔던 부분을 다시 정리하면서 복습하려고 만들었다. 그렇기 때문에 모든 내용을 다루지는 않는다. 코드를 보면서 문제를 해결할 때 어떻게 생각해야 하는지에 대한 부분을 중심으로 다루겠다.
1. k Nearest Neighbors
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
# Do not use np.linalg.norm(). #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists[i,:]=np.sqrt(np.sum(np.square(X[i]-self.X_train),axis=1))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return distsone loop 함수에서 내가 막혔던 것은 놀랍게도 dists[i,:]를 dists[i:] 라고 썼기 때문이다. 아주 바보가 따로없다...둘은 완전히 다른 표현인데, 정답인 dists[i,:]는 i 번째 행에서 모든 열을 뜻하고, dists[i:]는 i행부터 끝행까지를 의미한다.의미를 정확히 생각하고 코드를 적어야 할 것 같다.
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy, #
# nor use np.linalg.norm(). #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
test_squared = np.sum(np.square(X),axis = 1).reshape(-1,1)
train_squared = np.sum(np.square(self.X_train), axis = 1)
test_train_mul = -2*np.dot(X,self.X_train.T)
dists = np.sqrt(test_squared+train_squared+test_train_mul)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists 다음은 fully vectorized version이다. 이 vectorized version이라는 표현도 어색했는데, 찾아보니 벡터의 연산을 동시에 처리하는 것을 얘기한다고 한다. for문보다 속도가 압도적으로 빠르기 때문에 이 방식을 사용하는 것을 추천한다.
어쨌든 여기서는 아예 접근 자체를 어떻게 할 지 생각하지 못했다. 결론적으로 힌트에서 말한 matrix multiplication과 broadcast sum 2개를 이용하라는 것은 L2 distance 공식을 전개해서 생각하라는 뜻이었다. 코드를 통해서 자세히 알아보자.

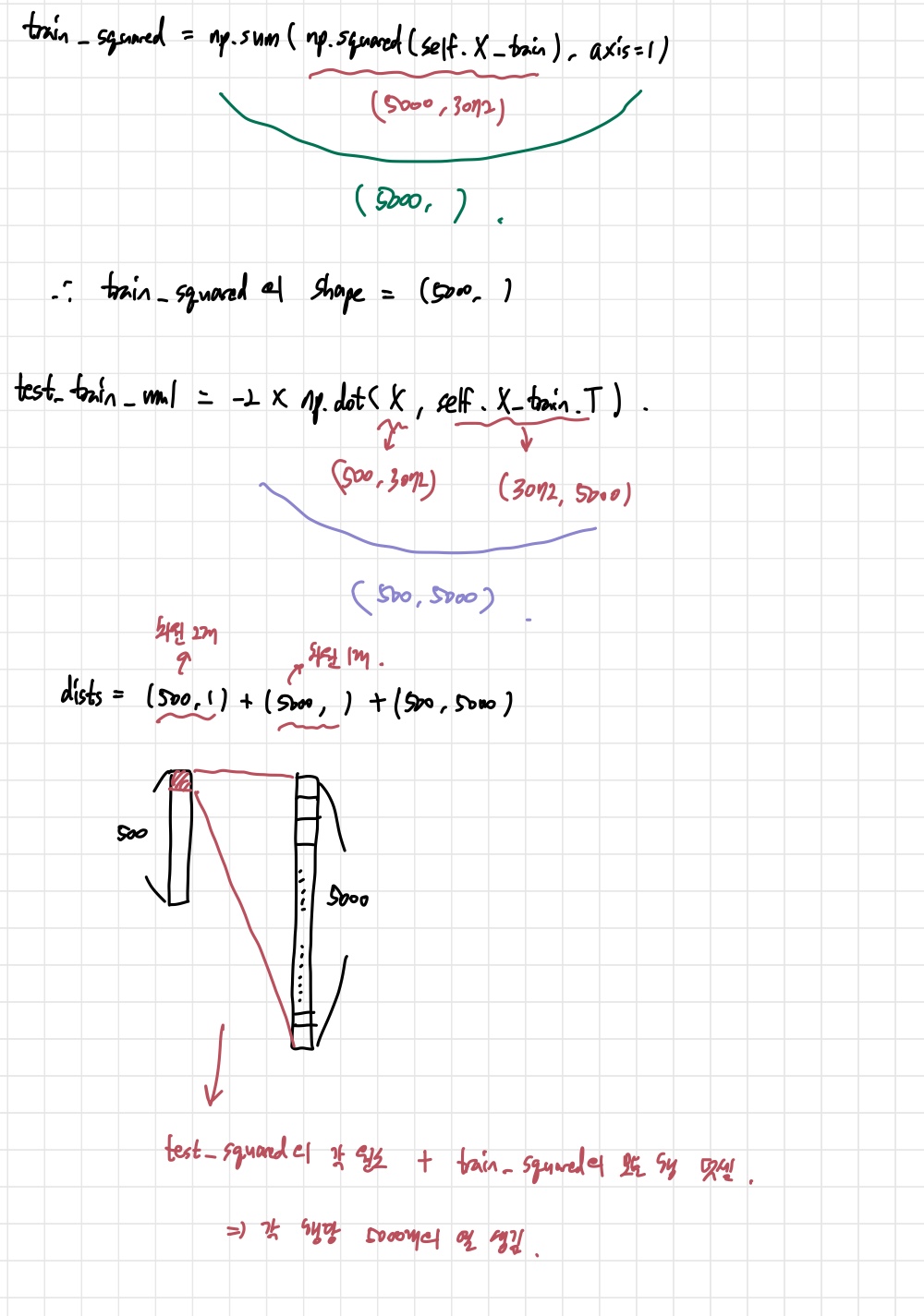
위의 사진은 각 과정에서 shape를 그린 것이다. 주목해야 할 것은 (r,1)과 (r,)의 차이이다. 전자는 2차원이고, 후자는 1개의 차원에 숫자들만 존재하는 것이다. 만약 두 개를 더한다면, 차원이 더 많은 (r,1)에 broadcasting 되는 것이다.
그리고 matrix multiplication에서 나는 np.dot을 사용했는데, np.matmul을 사용해도 된다. 그러나 계산하려는 행렬들이 3차원이 넘어가면 dot과 matmul의 계산 결과가 다르니 유의해서 사용해야 한다.
2. Cross validation
여기서는 다른 것보다 training set과 validation set 나누는 것이 가장 어려웠다. np.concatenate를 쓸 생각을 안 했던 것이 가장 큰 문제였다. 처음에는 음수 slicing으로 해결될 줄 알고 index 값들을 바꿔가면서 시도해보았다. 그러나 별로 소득이 없었고, 구글링을 했다. 이렇게 다 구글링할 거면 뭐하러 과제를 하냐 싶지만, 복습이라도 열심히 하려고 한다. 다음 과제부터는 새로운 함수들을 좀 찾아봐야겠다.
#*****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for k in k_choices:
k_to_accuracies[k]=[]
for j in range(num_folds):
trainXfolds=np.concatenate([x for num,x in enumerate(X_train_folds) if num!=j])
trainyfolds=np.concatenate([x for num,x in enumerate(y_train_folds) if num!=j])
valXfolds=X_train_folds[j]
valyfolds=y_train_folds[j]
classifier.train(trainXfolds,trainyfolds)
y_pred_fold=classifier.predict(valXfolds,k=k,num_loops=0)
acc=float(np.sum(y_pred_fold==valyfolds)/valXfolds.shape[0])
k_to_accuracies[k].append(acc)
#*****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****설명을 하자면, concatenate 안에 for문을 넣어서 해당 fold가 concatenate될지 말지 결정하는 방식으로 training set과 validation set을 나누었다. 솔직히 concatenate 안에 for문 넣을 수 있는지도 몰랐다. 코딩으로는 갈 길이 멀다...하여튼 그렇게 해서 문제는 해결됐다.
3. 기억해야 할 것들
마지막으로 외워서 쓸 일은 없을 것 같지만 과제에서 등장한 몇가지 함수들, 그리고 꼭 기억해야 하는 함수/문법만 몇 개 더 살펴보자.
1) np. bincount(a): 음이 아닌 수들이 배열 a에서 각각 몇 번 등장하는지 알려주는 배열을 반환한다. 최빈값 계산할 때 사용했다.
2) np.linarg.norm(a,n): 배열 a의 Ln norm을 계산해준다.
3) enumerate(a): 배열 a의 (index,element)를 반환 해준다.
4) np.flatnonzero(a or 조건문): 원소들 중에 0이 아닌 것들의 인덱스를 배열의 형태로 반환해준다.
5) range(start, end, step)
3)~5)는 자주 등장하니 외워두어야 할 것 같다.
