논문 리뷰(15) - Accelerating Image Super-Resolution Networks with Pixel-Level Classification

    이번 논문은 연세대학교 CIPLAB에서 ECCV 2024에 발표한 'Accelerating Image Super-Resolution Networks with Pixel-Level Classification'이라는 논문이다. 이 논문에서 다룬 모델의 이름은 PCSR(Pixel-level Classifier for Single Image Super-Resolution)이라고 불린다. 이전부터 관심이 있었던 Super Resolution에 관련된 내용인만큼 흥미롭게 읽었다.

1. 저자가 이루려고 한 것

1) 기존 연구의 트렌드

    저자가 짚어낸 기존 연구의 두 가지의 문제점에 대해 알아보자. 기존 SISR(Single Image Super-Resolution)은 patch-based method를 기반으로 한 방식들이 많았다. overlapping patch들로 이미지를 나눈 후, patch의 restoration difficulty에 따라 computing resource를 다르게 할당하였다. 연구가 진행되며 model의 capacity가 점점 커졌고, 이에 따라 computational cost도 자연스레 증가하여 현실에서 적용하기 어려운 상황이 되었다. 이것이 첫 번째 문제점이다. 이 문제를 해결하기 위해 lightweight, efficient 모델에 대한 논문들이 많이 나오게 되었다.
  두 번째는 large resolution image를 사용하면 image 크기가 작을 때에 비해 성능이 떨어진다는 것이다. large image는 계산 자원의 한계로 한 번에 처리하기가 어렵다. 따라서 overlapping patch로 나누고, 각 patch에 대해 따로따로 model을 적용하고 최종 output을 내야 한다.

2) PCSR이 해결하고자 한 문제

    위에서 언급한 대로 large image를 처리하기에는 한계가 있었다. 또, large image는 그 patch의 크기도 커지므로 하나의 patch 안에서도 각 pixel의 restoration difficulty가 다를 수 있다는 문제점도 있었다. 논문의 저자는 이를 해결하기 위해 pixel-level에서의 classification을 통해 SR process를 가속화시키는 아이디어를 제안한다. computational resource를 더욱 효율적으로 사용하여 pixel 단위에서 복원 난이도를 확인하고, 그에 맞는 upsampler에게 그 pixel을 할당하는 방식이다. 이렇게 pixel의 복원 난이도에 따라 upsampler를 다르게 하여 연산량을 줄이고자 도입한 것이 PCSR이다. 이제 PCSR에 대해 자세히 알아보자.

2. 주요 내용

1) Preliminary

    뒤에 등장할 수식능 이해하기 위해 논문에서 사용한 표현들을 정리하고 넘어갈 필요가 있다. 우리가 익히 알고 있는 SISR task의 목표는 LR image $I^{LR}$에서 HR image $I^{HR}$를 복원하는 식 $F$를 찾는 것이다. 이 관계는 아래 식으로 표현될 수 있다.

$I^{HR}= F(I^{LR};\theta)$

• $\theta$는 모델의 parameter

기존에 연구된 모델들은 대부분 Backbone(B) - Upsampler(U) 구조를 갖는다. backbone은 LR image에서 feature들을 뽑아내고, upsampler는 이를 이용해 HR를 복원하는 방식이다. 이는 아래 식으로 표현된다.

$Z= B(I^{LR};\theta_B), \ I^{HR}=U(Z;\theta_U)$

• $Z$는 추출된 feature,
• $\theta_B, \theta_U$는 각각 backbone과 upsampler의 parameter

보통 Upsampler는 CNN 기반의 모델들을 많이 사용한다. 그러나 계산량을 줄이기 위해 MLP(Multi-Layer Perceptron) 기반의 네트워크들을 사용할 수도 있다.

2) Network Architecture

    이제 PCSR의 네트워크 구조에 대해 알아보자. 기본적으로 backbone - classifier - upsampler 구조로 이루어져 있다.

i. Backbone

    Backbone은 LR image로부터 feature를 뽑아내는 역할을 하는 모델이다. PCSR에서의 backbone은 현존하는 어떤 SR network를 사용해도 무방하다고 한다. 모델의 capacity에 따라 FSRCNN, CARN, SRResNet 등을 사용할 수 있다. FSRCNN은 비교적 작은 모델, CARN은 중간 크기의 모델, SRResNet은 크기가 큰 모델이다. 이 밖에 다른 모델을 사용해도 된다.

ii. Classifier

    PCSR에서 사용하는 classifier는 비교적 lightweight한 모델이다. MLP 기반의 네트워크로, 각 pixel이 upsampler에 배정될 확률을 예측하는 것이 목적이다. 예를 들어 M개의 upsampler가 있다면, classifier는 특정 pixel의 복원 난이도를 기반으로 어떤 upsampler에 배정되면 좋을 지 예측하는 것이다. 가장 높은 확률 값을 갖는 upsampler에게 그 pixel을 배정한다.
    특정 pixel의 coordinate $x_q$가 주어졌을 때, classifier는 이 pixel을 가장 적합한 upsampler에게 배정하고, 이를 통해 성능을 최대한 유지하며 computational resource를 아껴서 사용할 수 있다.

• LR input image: $X \in \mathbb R^{h \times w \times 3}$
• $X$의 HR counterpart : $Y \in \mathbb R^{H \times W \times 3}$
• $\{y_i\}_{i=1,..HW}$ : HR space $Y$의 각 pixel의 coordinate(좌표)
• $\{Y(y_i)\}_{i=1...,HW}$ : 각 pixel의 RGB 값

위와 같이 input과 관련된 값들을 정의할 수 있다. 먼저 backbone에서 LR feature $Z \in \mathbb R^{h \times w \times D}$를 계산한다. 이때 upsampler의 개수(논문에서는 이를 class라고 표현한다.)를 M이라고 한다면, classifier C는 classification probability $p_i \in \mathbb R^M$를 계산한다. 이를 식으로 쓰면 아래와 같다.

$p_i = \sigma(C(Z,y_i;\theta_C))$

• $\sigma$ : softmax function

LR feature와 pixel의 coordinate를 입력으로 받아 MLP layer와 softmax를 거쳐 확률값을 얻는 것을 알 수 있다. upsampler별 확률이 나와야 하는 만큼 output의 차원이 $M$이라는 것이 중요하다.

iii. Upsampler

    Upsampler는 기본적으로 pixel-level processing에 적합한 LIIF를 사용한다. 먼저 HR space의 좌표인 $y_i$를 LR space의 좌표인 $\hat {y_i} \in \mathbb R^2$으로 mapping하도록 한다.

• $z_i^* \in \mathbb R^D$ : LR feature $Z$ 중 $\hat{y_i}$에 가장 가까운(Euclidean Distance 기준) feature.
• $v_i^* \in \mathbb R^2$ : $z_i^*$에 해당하는 좌표값

위와 같이 term들을 정의할 때, Upsampling process는 아래와 같이 쓸 수 있다.

$I^{SR}(y_i) = U(Z,y_i;\theta_U) = U([z_i^*, \hat{y_i}- v_i^*];\theta_U)$

• 이때, $I^{SR}(y_i) \in \mathbb R^3$ : $y_i$에서의 RGB value.
• [$\dots$] : concat 연산

위의 식에서 upsampler는 LR feature 중 $\hat{y_i}$에 제일 가까운 feature ($z_i^*$)와 query pixel의 LR space 좌표와 가장 가까운 feature의 거리를 나타내는 $\hat{y_i}- v_i^*$를 concat한다. 최종 output인 $I^{SR}$은 모든 pixel 좌표 $\{y_i\}_{i=1,..HW}$ 대해 RGB 값을 다 얻은 후 이 결과를 다 합쳐서 나오게 된다.
  이 부분이 PCSR의 핵심인 것 같다. 기존의 SR 모델들이 fixed size에 대한 upsampling만 할 수 있었다면, 이렇게 feature와 그 좌표를 같이 모델에 주기 때문에 앞서 언급한 continuous SR이 가능해지는 것이다.

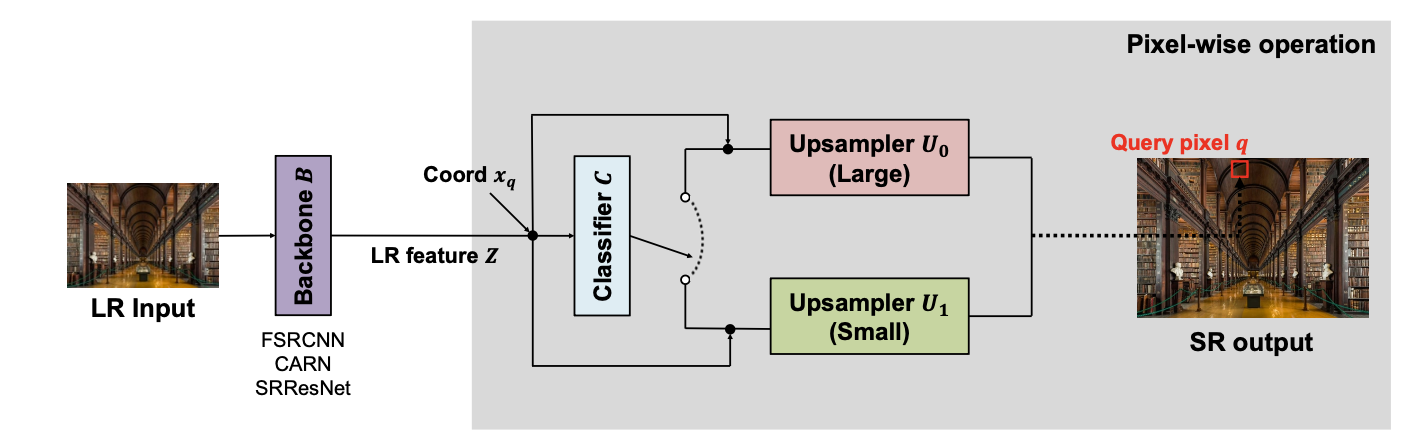
위의 사진은 PCSR의 구조도이다. 그림의 간단함을 위해 upsampler의 개수(=class) M=2로 설정한 예시를 보여주고 있다.

3) Training

    훈련 시에는 query pixel을 M개의 upsampler에게 feed-forward 연산을 하며, 각각의 output을 합쳐 backprop에 이용한다. 식은 아래와 같다.

$\hat {Y}(y_i) = \sum^{M-1}_{j=0} p_{i,j} \times U_j(Z,y_i;\theta_{U_j})$

• $\hat {Y}(y_i) \in \mathbb R^3$ : $y_i$에서의 RGB output
• $p_{i,j}$ : 해당 query pixel의 upsampler $U_j$에서의 확률

Loss function

    Loss function은 Reconstruction Loss와 Average Loss 두 가지를 같이 사용한다. Reconstruction Loss $L_{recon}$는 예측된 output RGB 값과 target RGB 값 간의 L1 loss이다. 그런데, target을 어떻게 설정했는지에 대해 살펴볼 필요가 있다.

$\text{target} = \text{(GT HR patch) - (bilinear upsampled LR patch)}$

일반적인 방법인 GT HR patch을 사용하지 않고 위와 같이 target 값을 설정하는 이유는 classifier가 high frequency 정보에 집중하기 위해서이다. 여기서 high frequency는 급격한 색/ 밝기 변화가 일어나는 부분(ex. edge, detail, sharpness)을, low frequency는 완만한 색 변화가 일어나는 부분(ex. smooth, blurry)을 의미한다. GT HR patch에서 LR upsampled patch를 빼면 결과적으로 high frequency에 해당하는 부분만 남고, 이를 target으로 둔다면 capacity가 작은 모델에서도 성능이 떨어지지 않는 효율적인 학습이 이루어질 수 있을 것이다. Reconstruction Loss의 식은 아래와 같다.

$L_{recon} = \sum^{HW}_{i=1}|(Y(y_i)-up X(y_i))-\hat{Y}(y_i)|$

• $up X(y_i)$ : 위치 $y_i$에서의 bilinear upsampled LR patch

    다음은 Average Loss $L_{avg}$이다. average loss에서는 M개의 upsampler들에 균등하게(uniform) pixel을 배분한다. 식은 아래와 같다.

$L_{avg} = \sum_{j=1}^M |\sum_{n=1}^N \sum_{i=1}^{HW} p_{n,i,j}- {NHW \over M}|$

• $p_{n,i,j}$ : n번째 HR image(N은 batch dimension임)의 i번째 pixel의 j번째 upsampler에 대한 probability.

여기서 각 확률 값은 각 upsampler에 할당되는 pixel의 개수를 나타내는 값으로 사용한다. 이 말이 헷갈릴 수 있지만, 특정 upsampler에 들어가야 하는 pixel이라면 그 upsampler에서 확률 값이 1에 가까울 것이기 때문에 확률이 pixel 개수를 나타내는 지표로 사용되어도 괜찮다. target 값은 $NHW \over M$로 설정했는데, 이는 uniform하게 나눈다면 각 upsampler가 할당받아야 할 pixel의 개수를 의미한다. 이렇게 Reconstruction Loss와 Average Loss에 대해 알아봤다. 최종 total loss는 아래와 같다.

$L=w_{recon} \times L_{recon} + w_{avg} \times L_{avg}$

두 개의 loss의 weighted sum인 것이다.

    훈련을 하려면 backbone, classifier, M개의 upsampler를 모두 학습시켜야 한다. 이들을 모두 동시에 훈련시키는 것은 불안정한 학습이 될 가능성이 높다. 따라서 저자들은 multi-stage training을 도입해서 사용한다. upsampler의 capacity가 큰 것부터 작은 순서대로 $U_0,..U_{M-1}$이라고 하면, 모델의 최고 성능은 backbone과 가장 큰 upsampler인 $U_0$에 의해 결정될 것이다. 따라서 먼저 $\{B, U_0\}$를 reconstruction loss만 사용해서 훈련시킨다. 그 이후 $j=1,..M-1$ 까지는 아래 과정들을 반복한다.

1. 이전에 훈련된 $\{B,U_0,...,U_{j-1}\}$을 freeze한다.
2. $U_j$를 backbone $B$에 붙인다. ( $j=1$일 때는 Classifier $C$도 함께 붙여준다.)
3. $\{U_j,C\}$를 total loss를 사용해 함께 학습시킨다.

4) Inference

    다음은 inference이다. 대부분의 과정은 Training과 동일하지만, query pixel이 classification 확률에 따라 특정 upsampler에 배정된다는 사실만 다르다. 이러한 query pixel의 배정은 FLOPs에 따라 결정된다. 먼저 각 upsampler들이 필요로 하는 FLOPs 수를 미리 계산해놓는다.

$\text{cost}(U_j) = \sigma (\text{flops}(B;(h_0,w_0)) + \text{flops}(U_j;(h_0,w_0)))$

• $\sigma$ : softmax function
• $(h_0,w_0)$ : fixed resolution을 의미.

이후의 좌표 $y_i$에서의 pixel의 upsampler 할당은 아래와 같은 식으로 이루어진다.

$argmax_j {p_{i,j} \over [cost(U_j)]^k}$

• k : hyperparameter
• $p_{i,j}$ : 좌표 $y_i$에서의 query pixel이 upsampler $U_j$에 배정될 확률

만약 $k$의 크기가 작다면 capacity가 큰 upsampler에 더 많은 pixel들이 할당될 것이고, 그 반대라면 capacity가 작은 upsampler에 더 많은 pixel이 할당될 것이다. 예를 들어 이해해보자.

$U_j$가 heavy upsampler이고, k 값이 크다고 해보자 .

• $cost(U_j)$는 클 것이다. 그러나 여기서 주의해야 하는 것이, $cost(U_j)$의 범위가 $[0,1]$이라는 것이다. (softmax output)
• k가 크므로, $[cost(U_j)]^k$는 작을 것이다.
• 따라서 ${p_{i,j} \over [cost(U_j)]^k}$ 는 클 것이다.

이와 반대로 light upsampler의 경우도 이와 같은 방법으로 이해하면 k의 크기에 따라 heavy/lightweight upsampler에 pixel이 더 많이 할당되는지에 대한 원리를 파악할 수 있다.

ADM (Adaptive Decision Making)

    ADM은 저자들이 사용자들에게 제공하는 추가적인 기능이다. pixel을 전체 이미지들을 보고 자동으로 알맞은 upsampler들에게 할당해주는 역할인데, 자세하게는 소개하지 않으려고 한다. restoration difficulty를 계산하고 clustering algorithm을 이용해 M개의 upsampler에 배정한다.

Pixel-wise Refinement

    PCSR을 통해 pixel들의 RGB값을 예측하다 보면 SR output이 부자연스럽게 보이는 문제점이 생긴다. 같은 patch 안에서도 이웃한 pixel이 서로 다른 capacity를 가진 upsampler에게 배정될 수 있다 보니 생기는 문제이다. 이를 해결하기 위한 것이 Pixel-wise Refinement이다. $U_0,..U_{(M+1)/2}$를 heavy upsampler, 나머지를 light upsampler라고 하면, pixel-wise refinement는 이웃한 pixel들이 서로 다른 타입(heavy/lightweight)의 upsampler에게 배정되어 output이 나왔을 경우에만 적용된다. (예를 들어 특정 pixel이 $[(M+ 1)/2] \leq j <M$, 즉 lightweight upsampler에 배정되었는데 그 옆의 pixel이 heavy한 upsampler인 $0 \leq j <[(M+ 1)/2]$에 배정된 경우를 말하는 것이다.) 이러한 경우에 그 pixel의 RGB 값을 이웃하는 pixel들의 평균으로 대체하는 것이다. (평균을 계산할 때 자기 자신도 포함한다.) Pixel-wise refinement 알고리즘은 추가적인 forward process를 사용하지 않고 효과적으로 부자연스러운 artifact들을 개선하는 효율적인 방법론이다.

5) Experiments

    마지막으로 실험들을 살펴보자. 기본적인 실험 세팅은 ClassSR와 ARM과 동일하게 맞추고 진행했다고 한다.

Training

• Dataset : DIV2K (index 0~800 cropped into 1.59M 32x32 LR subimages)
• Data augmentation : Flipping, random rotation
• Backbone : FSRCNN, CARN, SRResNet
• batch size=16, lr= 0.001(FSRCNN), 0.0002(CARN, SRResNet), Cosine Annealing scheduling
• Adam optimizer
• original model & PCSR 둘 다 2000K iterations, PCSR의 단계적인 training은 500K.
• PCSR : backbone에서 original model들과 PSNR, FLOPs를 맞추기 위해 hidden dimension fine-tuning, upsampler의 MLP size 조정

Evaluation

• Dataset : Test2K,Test4K, Test8K (downsampled from DIV8K), Urban100 (larger images)
• Evaluation Metrics : PSNR(RGB space), FLOPs (measured in full image)

Results

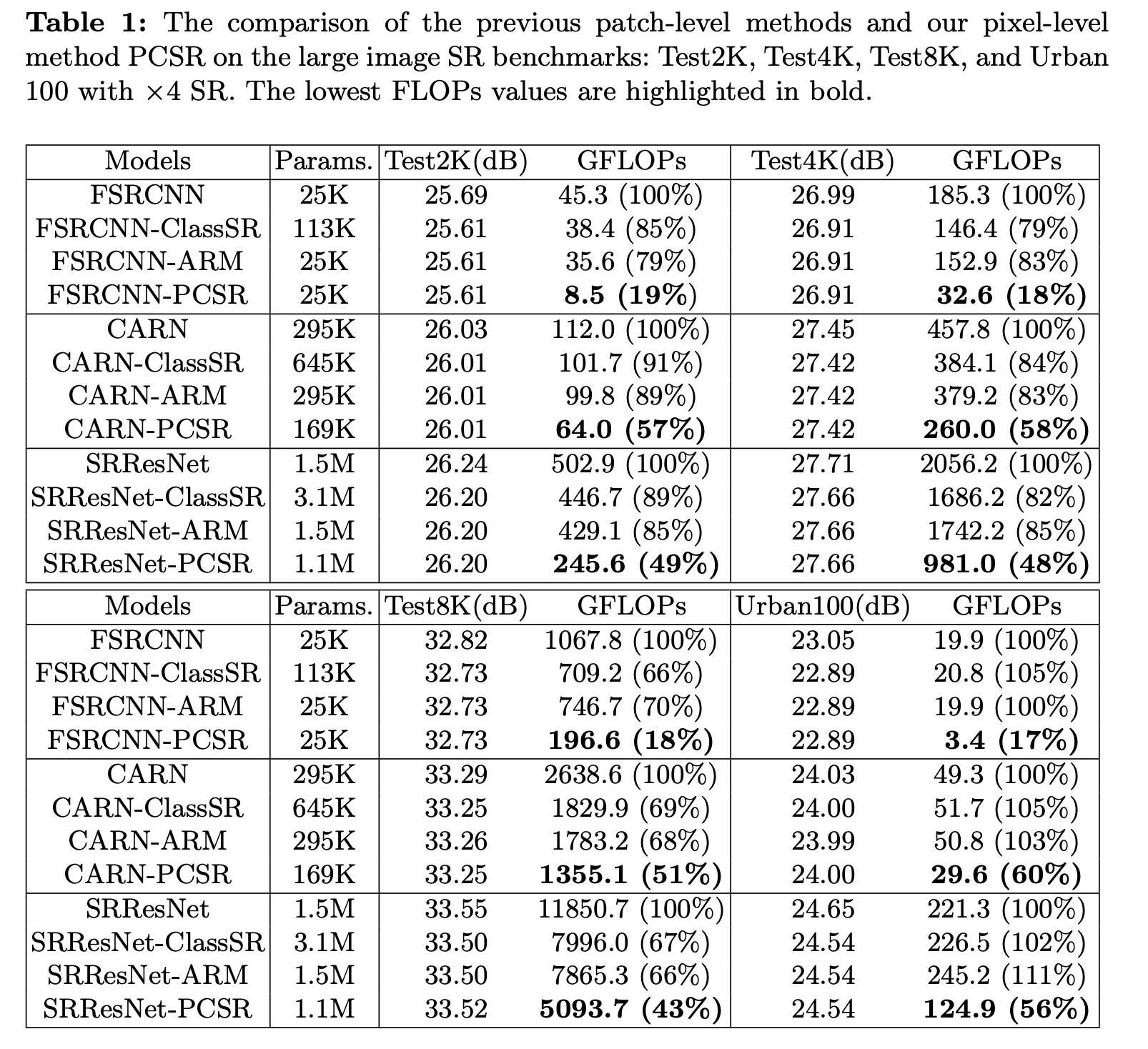
위의 표를 보면, PCSR은 PSNR을 original 모델들과 비슷한 수준으로 유지하며 FLOPs 수를 확연하게 줄인 것을 볼 수 있다.

육안으로 보기에도 기존의 방법들이 잘 복원하지 못했던 얇은 선과 같은 디테일들을 PCSR은 잘 살려서 복원한다.

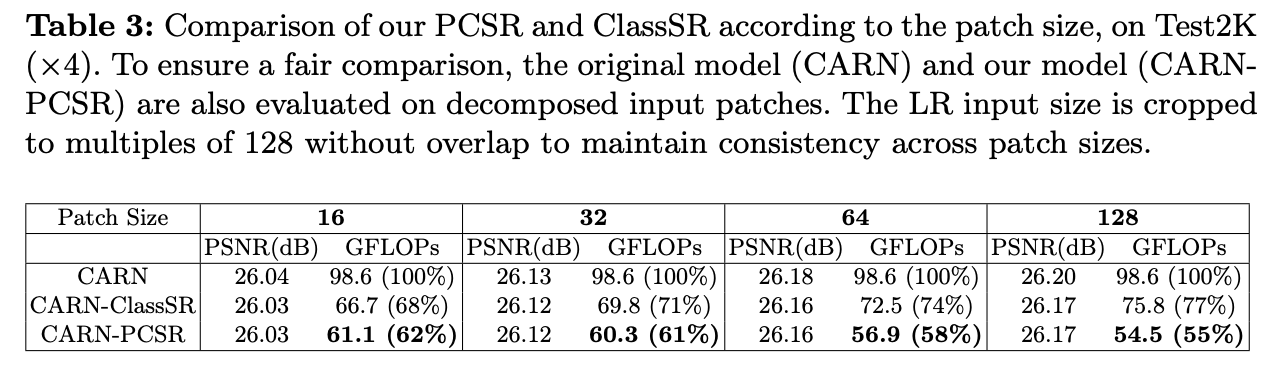
또한, patch size가 커질수록 기존의 방법론들보다 FLOPs 수가 더 큰 비율로 감소하는 것 또한 확인할 수 있다.

3. 논문 내용의 실용성

    이 논문은 large scale image SR 측면에서 최소한의 성능 감소로 효율성을 높였다는 것에 의의가 있다. 기존의 SR model들의 덩치가 커지면서 실제 서비스나 현실에서 그 모델들을 이용하기는 쉽지 않았으나, computational resource를 효율적으로 사용할 수 있는 방법론을 제시했다. 모델에 따라 다르지만 FLOPs 수를 대부분 50%에 가까운 비율로 줄였다는 것도 주목할 만하다. classifier는 backbone에서 나온 LR feature를 사용하기 때문에 모델 FLOPs lower bound가 backbone의 크기에 의해 정해진다는 것이 한계이다. 이는 영역이 거의 바뀌지 않는 flat region에서의 계산 자원 낭비로 이루어질 수 있을 것이다. 이를 해결한다면 조금 더 좋은 성능과 효율성을 갖춘 모델이 만들어질 것이라고 생각한다.

4. 더 찾아볼 내용

    논문을 읽으며 등장한 SR 논문들이 꽤 많다. 이들을 차례차례 읽어볼 필요가 있을 것 같다.

• LIIF
• SwinIR (논문에 등장하진 않았지만 읽어보려고 한다.)
• ClassSR
• CARN