논문 리뷰(2)- Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

    이번에 살펴볼 논문은 2015년에 제안된 'Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift' 라는 논문이다. 인공지능을 공부하다보면 자주 마주치게 되는 주제이다. 나는 cs231n 과제 2에서 batch normalization을 구현하기 위해 논문을 참고했다. 앞으로 어떻게 논문을 정리할지 고민하다가, 논문 내용을 그대로 서술하는 것보다는 Andrew Ng 교수님이 추천하신 방법대로 정리해보려고 한다.

1. 저자가 이루려고 한 것

    저자가 batch normalization을 통해 이루고자 했던 것은 네트워크 훈련 시의 activation value의 distribution을 stable하게 만들어 Internal Covariate Shift 문제를 해결하는 것이었다. 이를 해결함으로써 DNN(Deep Neural Network) 훈련 시에 learning rate를 상대적으로 높이는 것을 가능하게 하고, parameter의 initialization에 대한 민감도도 낮추며 dropout을 사용하지 않아도 된다. 결과적으로 훈련 시간을 줄이는 것이 이 연구의 주된 목적이었다고 볼 수 있다.

2. 주요 내용

1) Towards Reducing Internal Covariate Shift

    먼저 Internal Covariate Shift의 정의를 알아보자. 네트워크의 훈련 과정 중에 parameter 값들이 변함에 따라 activation들의 distribution이 변하게 되는데, 이와 같은 현상을 Internal Covariate Shift라고 한다. 이 현상이 네트워크에 좋지 않은 이유는 각 layer의 input distribution들이 바뀌며 parameter들이 이 변화에 적응해야 하기 때문이다. 따라서 Internal Covariate Shift를 줄일 수 있으면, training 속도가 빨라지는데 도움을 줄 것이다. 쉽게 말해 distribution이 변하는 것을 막겠다는 뜻이다.
  사용해볼 수 있는 하나의 방식으로 whitened input이 있다. 여기서 whitened는 zero mean, unit variance, decorrelated를 뜻한다. 이렇게 하면 nework training이 더 빨리 수렴한다고 알려져 있다.(LeCun et al. 1998b; Wiesler&Ney 2011) 이에 따라 모든 layer에 whitened input을 적용하면 성능이 더 좋아지고 우리가 원하는 fixed distribution에 가까워질 것 같지만, 실제로는 그렇지 않다. 이 방법이 기존의 optimization 방식인 gradient descent와 같이 사용된다면 오히려 gradient descent step에 안 좋은 영향을 주게 된다는 것이다.

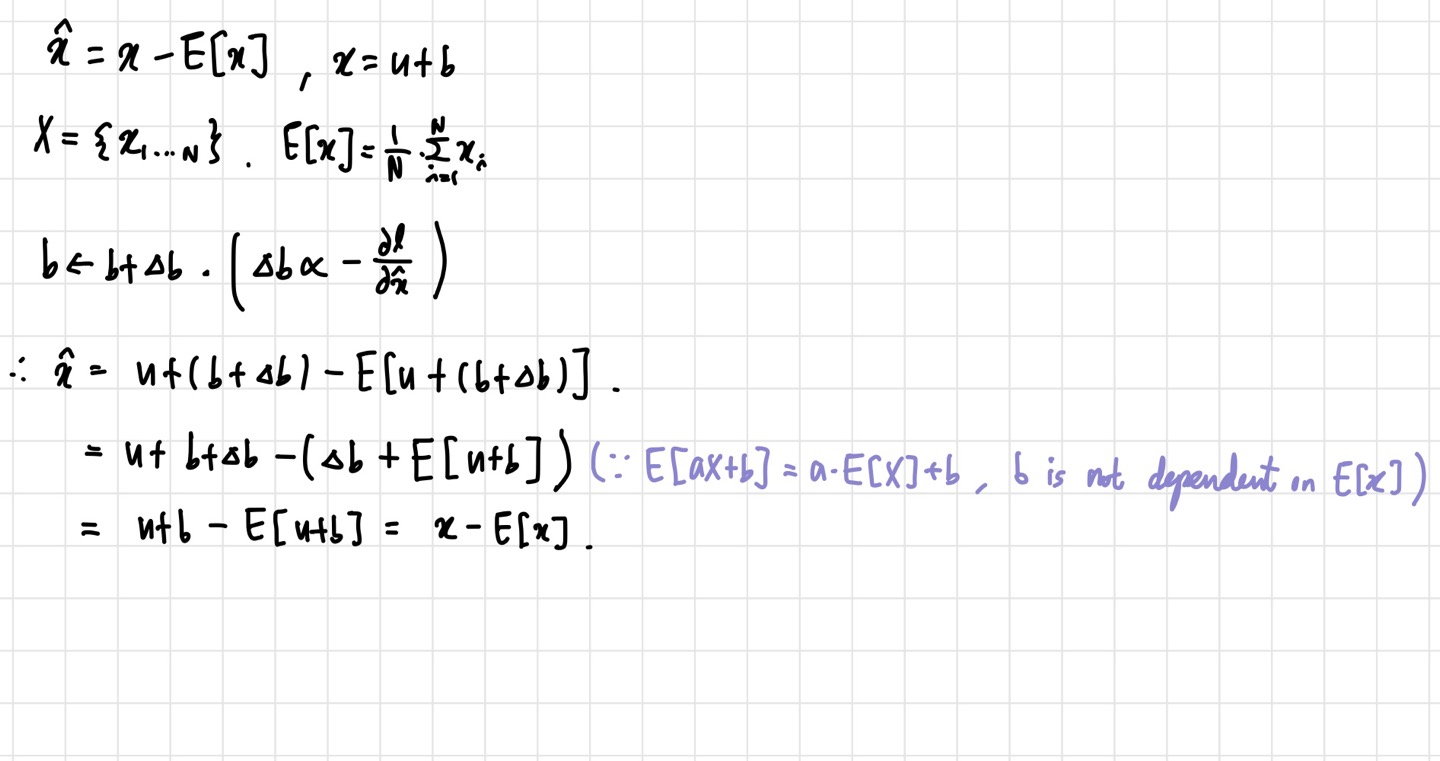
    위의 식에서 $u$: input, $b$:bias를 의미한다. 예시를 보면, $b$를 update하고 난 뒤에도 output에 아무런 영향을 미치지 못하며, $\hat{x}$의 값은 같게 나온다. 여기에 추가로 activation을 scaling할 경우, 이 문제는 더 심각해진다. 이와 같은 방법의 문제점은 gradient descent가 normalization이 같이 이루어지고 있다는 것을 고려하지 않는다는 것이다. 이를 해결하기 위해, 저자는 네트워크가 항상 desired distribution을 얻는 것이 중요하다고 주장한다. 이렇게 하면 loss의 parameter에 대한 gradient들이 normalization을 고려하게 할 수 있다.

X는 training data에서 input들의 집합

    Normalization term은 위 사진과 같이 쓸 수 있다. 주의할 점은 $\hat{x}$이 training example $x$뿐만 아니라 $X$의 영향도 받는다는 것이다. 그렇기 때문에 backprop시에 Jacobian을 계산해야 한다.

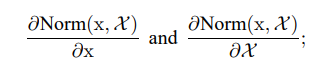
    이 방법은 Covariance matrix 계산을 동반하기 때문에 computation expensive한 측면을 가지고 있다. 따라서 저자는 각 parameter update마다 전체 training set을 분석하지 않아도 되고, 미분 가능하고, 간소화된 방법으로 normalization을 진행하는 방법을 제안한다.

2) Normalizaiton via Mini-Batch Statistics

    앞서 말한 simplification은 크게 두 가지로 구성되어 있다. 첫 번째는 각 scalar feature에 대해 독립적으로 normalization을 진행해 zero mean, unit variance를 만든다.

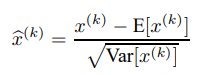
    위와 같은 과정을 각 차원별로 진행하는 것이다. 이 방법은 모델의 수렴 속도를 증가시키는 것으로 알려져 있다. (LeCun et al. 1998b) 이때 $x^{(k)}$의 평균과 분산은 training set에서 계산한다. 여기서 짚고 넘어가야 할 것은 이 방법이 가지는 문제점도 존재한다는 것이다. 예를 들어 sigmoid의 경우, normalization 결과 input들이 sigmoid의 linear regime에 국한되어 있게 된다. data에 nonlinearity를 주기 위해 activation function을 사용하는데, 정작 linear한 범위에서 input이 존재하게 되는 것이다. 이 문제를 해결하기 위해 아래 사진과 같이 scale value/ shift value를 이용한다.

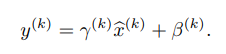
    이때, gamma와 beta 값은 learnable parameter이다. 그런데 만약 원래 distribution이 가장 최적의 분포였다면, gamma는 $x^{(k)}$의 표준편차로, beta는 $x^{(k)}$의 평균으로 설정하면 된다.
  두 번째 방법은 batch 단위로 normalization을 진행하는 것이다. 기존 normalization의 경우, 전체 dataset에 대해 진행하였다. 그러나 SGD는 batch 단위로 optimization을 진행하기 때문에 효율적이지 못하다. 그래서 normalization도 batch 단위로 하는 것이다. SGD에서 각 mini-batch 별로 mean과 variance에 대한 추정을 하기 때문에, 이를 이용해 normalization도 batch 단위로 진행할 수 있다. 이를 Batch normalizing transform이라고 한다.

normalize 단계에서 입실론 값은 numerical stability를 위해서 도입함.

    BN transform은 어떤 activation에도 적용될 수 있다. 이 방법을 이용하면 differentiable한 transformation이 가능하다는 것도 아래 사진의 chain rule을 통해 알 수 있다.

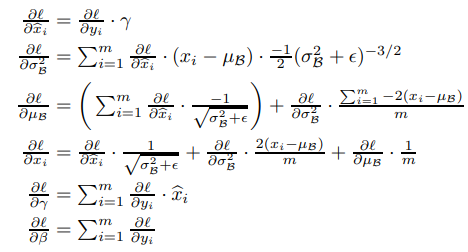
    이렇게 훈련이 끝나고 inference 때는, 훈련때 사용한 mini batch statistic을 사용하지 않는다. 일단 zero mean과 unit variance를 만들어주기 위해 아래의 식을 통해 normalization을 해준다.

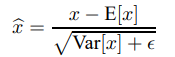
    그리고 여기서 중요한 개념인 moving average를 이용해 inference에 사용할 mean과 variance를 결정한다. 훈련하는 동안 저장해놓은 각 layer에서의 평균과 분산 각각의 평균을 구해 사용하는 것이다. 이렇게 구한 평균들의 평균/ 분산들의 평균이 inference에서 사용된다.

3) Batch Normalized Convolutional Networks

    CNN에서도 batch normalization을 적용할 수 있다. 식의 구성 방식은 비슷하다.

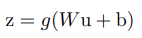
    위와 같은 식을 사용하는데, $W,b$는 learnable parameters, $g$는 nonlinearity를 뜻한다. BN은 nonlinearity 바로 직전에 적용한다. 즉, $x=Wu+b$를 normalize 한다는 뜻이다. $Wu+b$의 분포가 더 symmetric하고 더 gaussian스러운 분포라고 한다. 마찬가지로 BN을 적용했을 때 더 stable한 distribution을 갖는다.
  Convolutional Layer의 경우, normalization이 convolutional property를 따르게 해야 한다. 그래야 같은 feature map의 각기 다른 원소들이 같은 방식으로 normalize 될 수 있기 때문이다. 이를 위해서 batch를 다시 설정한다. batch size가 $m$이고, feature map size가 $p*q$라면, 우리는 batch size로 $m'=m*p*q$를 사용한다. 감마와 베타가 차원별로 있는 것은 위의 내용과 동일하다. batch size를 제외하고는 비슷한 방식으로 normalization이 진행된다.

4) Batch Normalization enables higher learning rates

    전통적인 DNN은 너무 높은 learning rate를 사용할 경우 gradient가 explode 혹은 vanish할 수 있다. 또, 성능이 좋지 않은 local minima에 끼어버릴 수도 있다. 네트워크의 layer 수가 많아질 수록 이럴 가능성은 더욱 증가한다. 그러나 앞서 살펴봤던 BN을 사용함으로서 이 문제를 해결할 수 있다. BN은 네트워크의 parameter의 작은 변화가 amplify되어 gradient의 큰 영향을 미치는 것을 방지해준다. 또한, 높은 lr의 경우 layer parameter들의 scale을 키우게 되는데,BN을 사용함으로써 parameter scale에도 더 resilient하게 된다.

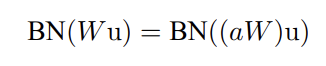
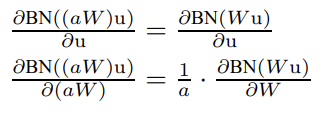
    위의 사진의 식을 통해 scale $a$는 Jacobian에 아무런 영향을 주지 못한다는 것을 알 수 있다. 때문에 Backprop시에도 문제가 없다. 큰 weight들은 작은 gradient로 이어진다는 점에서 parameter growth를 안정화 시킨다는 것을 확인할 수 있다.
BN은 실험 결과, 네트워크를 generalization하는 효과가 있다는 것이 밝혀졌다. BN을 사용하는 경우, dropout은 사용하지 않아도 된다고 한다.

3. 논문 내용의 실용성

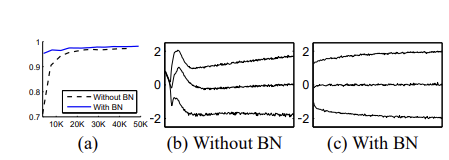
    위의 그래프들은 MNIST를 사용했을 때 BN 사용 여부에 따른 네트워크의 변화들을 나타낸 것이다. 네트워크는 3-layer network였고, 모두 FC layer를 사용했다. 구체적으로 (a)는 training step 수에 따라 BN을 사용한/사용하지 않은 네트워크의 test accurcy를 나타낸 것이다. BN을 사용한 네트워크가 더 빠르게 training 되고 더 높은 정확도를 얻는 것을 볼 수 있다. (b),(c)는 BN을 사용/사용하지 않았을 때의 input distribution의 변화를 나타낸 것이다.(하나의 activation을 기준으로 그래프를 그린 것이다.) BN을 사용한 네트워크의 distribution이 더 stable한 것을 알 수 있다.
  ImageNet을 Inception Network를 통해서 훈련시키는 실험도 진행하였다. 네트워크는 여러 convolutional layer들과 pooling layer, 그리고 softmax layer로 구성되어 있다. BN은 모든 nonlinearity에 적용되었다. 여러 가지를 바꾸어 가며 5개의 모델들을 비교했을 때, 아래의 그래프와 같이 결과가 나온다.

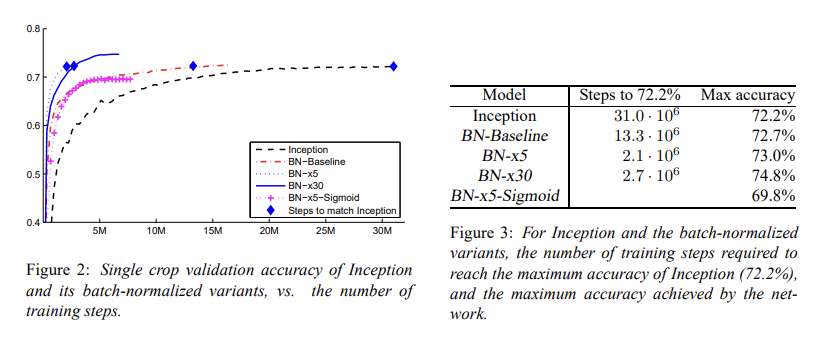
    BN-x5의 경우 Inception보다 14배 적은 step으로 비슷한 max accuracy를 얻을 수 있다. 그리고 훈련이 잘 되지 않던 시드모이드를 이용한 네트워크도 BN 사용 시 69.8%의 max accuracy가 나오는 것을 볼 수 있다.
  인공지능을 배운다면 꽤 중요하게 다루는 내용이고 사용했을 때 DNN의 성능 개선이 확실히 되는 것을 확인할 수 있기 때문에 중요한 논문이라고 생각한다.

4. 찾아볼 레퍼런스

1) Covariance matrix/ correlation-논문에 등장한 수학적인 내용이 잘 이해되지 않아 찾아봐야겠다.
2) singular values- 기본적으로 선형대수 내용이 잘 기억이 나지 않아 복습할 필요성을 느꼈다.
3) LeCun et al. 1998b - https://cseweb.ucsd.edu/classes/wi08/cse253/Handouts/lecun-98b.pdf

5. 정리

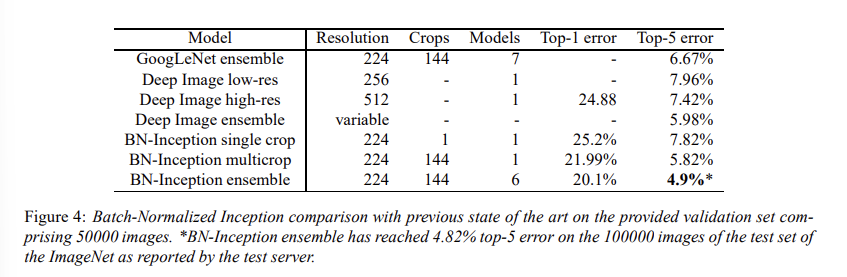
    BN을 사용할 경우, 전통적인 DNN에서는 사용하기 힘들었던 높은 learning rate들을 사용할 수 있었고, parameter initialization에 대한 민감도도 비교적 적어져 훈련하기에 용이했다. 또, BN이 일종의 regularizer 역할을 하기도 하기 때문에 dropout을 사용하지 않아도 되었다. 각 layer input의 Internal Covariate Shift를 줄임으로써 그 distribution을 stable하게 만들어준 것이 훈련 속도를 높이는 데 중요한 역할을 했던 것 같다. 결론적으로 BN을 사용하고 ensemble을 적용할 경우, 당시의 SOTA 네트워크보다 더 좋은 성능인 top-5 error 4.9%를 달성할 수 있었다.
  논문을 제대로 읽어본 것은 이번이 처음인데, 어떻게 이 아이디어를 얻게 되었나를 위주로 생각하면서 읽었던 것 같다. 그래도 저자가 하고자 하는 이야기를 어느 정도 알았음에 나름 만족한다. 다만 수학적인 기초를 조금 다져야 할 필요가 있다는 생각이 들었다.