이번에 살펴볼 논문은 2014년에 Dropout을 제안한 "Improving neural networks by preventing co-adaptation of feature detectors", Hinton et al. 이다. Dropout은 현재에도 overfitting을 방지하기 위한 도구로 많이 사용하기 때문에 알아둘 필요가 있을 것 같다. 인공지능 강의를 들으면 한 번쯤 들어보는 개념 중 하나이다. 논문 분량이 꽤 많아 정리가 길어질 것 같다.
1. 저자가 이루려고 한 것
Deep Neural network들은 복잡한 문제들을 해결할 수 있는 좋은 도구이다. 그러나 모델의 capacity가 큰만큼 파라미터 수도 많기 때문에 overfitting이 발생하기 쉽다. 우리가 사용할 수 있는 dataset의 크기도 모델의 복잡도를 해결하기에 적은 경우도 있고, 훈련 속도도 느린 것은 큰 문제다. 저자는 DNN에서의 overfitting 문제를 해결하는 방법 중 하나로 'Dropout'을 제안한다. Dropout을 DNN에 적용한 결과, 다양한 분야의 dataset에서 error rate를 낮춰주는 효과를 얻을 수 있었고, 덕분에 dropout이 여러 분야의 dataset에 대한 general한 해결책이 될 수 있다는 결론을 얻었다. 또한, model combination이 DNN에서는 특히 더 computationally expensive하기 때문에 dropout이 model combination을 대신할 수 있는 좋은 방법이라고도 주장한다.
2. 주요 내용
1) Introduction
DNN을 훈련할 때, 모델은 overfittting에 빠지기 쉽다. 많은 파라미터 수에 비해 구할 수 있는 training data에는 한계가 있기 때문에 이러한 문제가 생기는 것이다. 이전에 overfitting을 해결하기 위해 사용한 방법들에는 validaiton accuracy가 더 이상 좋아지지 않을때 훈련을 멈추는 early stop과 L1,L2 regularization 등이 있다. 또한, 계산량의 제한이 없다면 regularization method로 가장 좋은 방법은 가능한 모든 parameter 조합으로 얻은 prediction들에 weighted average를 취해주는 것이다. weighting은 training data가 주어졌을 때의 사후확률을 이용해서 해준다. 그러나 현실에서 이렇게 많은 계산량은 감당할 수 없다. 때문에 적은 계산량을 가지고 위의 방법과 비슷한 효과를 줄 수 있다면 이상적일 것이다.
이러한 효과를 줄 수 있는 방법이 Dropout이다. 단어 그대로, 훈련 시에 노드들을 일정한 확률(p)로 키는 것이다. 어떤 노드들이 꺼질지는 랜덤하게 정해진다. 보통 input unit들에게는 0.8, 나머지 unit들은 0.5로 p를 지정하는 것이 일반적이다. 여기서 p는 각 unit이 retain될 확률을 의미한다. 이렇게 랜덤하게 unit들이 사라지고 난 뒤의 네트워크를 thinned network라고 한다. 만약 네트워크에 unit이 n개라면, 가능한 thinned network는 2^n개이다. 각 training case 마다 p를 이용해 thinned network가 새로 만들어지는데, 이 네트워크들의 weight는 공유된다. 가능한 2^n개의 network들은 각각 훈련에 사용되는 횟수가 상당히 적을 것이다.
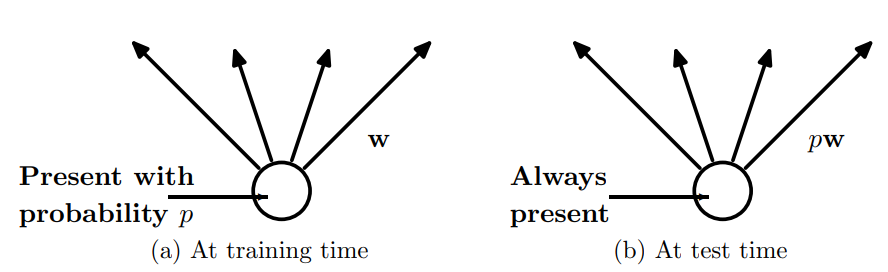
훈련 시에 하나의 unit이 네트워크에 사용될 확률 p를 갖는다. 이 말은 전체 training 중에 p의 확률만 그 unit이 사용된다는 뜻이다. 그런데 test time에는 unit이 항상 존재한다. weight들은 training 때의 상황에 맞춰서 update 되었기 때문에, 만약 test time에도 똑같은 scale의 weight들을 가지고 output을 낸다면 정확도가 상당히 떨어질 것이다. training time과 test time의 output scale을 맞춰주기 위해 그 unit의 weight들을 pw로 rescale해준다. 위의 사진을 보면 조금 더 직관적으로 이해가 가능할 것 같다.
2) Motivation
Dropout은 신기하게도 유성 생식에서 아이디어를 얻어서 만들어졌다고 한다. 유성 생식을 하는 생물은 유전자의 반은 아빠에게, 나머지 반은 엄마에게 받는다. 언뜻 보면 무성 생식이 생존에 유리한 부모의 유전자를 그대로 받아 더 유리할 것 같지만, 그렇지 않다고 한다. 실제로 고등 생명체들이 진화한 형태도 유성 생식이다. randomness를 더해 유전자를 받는 유성 생식이 환경에 더 robust하게 진화했다는 것이다. 결과적으로 유전자들 사이의 co-adaptation을 줄인 것이 robustness에 일조한 것이다. 이와 비슷하게게 저자들은 Neural network에서도 각 hidden unit이 다른 hidden unit의 도움 없이 의미 있는 feature들을 만들어 내 robustness를 증가시킬 수 있다는 생각을 떠올렸다.
3) Model Description
이제 dropout을 적용한 neural network 모델에 대해서 알아보자. L개의 hidden layer들이 있고,
로 각 layer들이 표현된다고 할 때, dropout을 사용하지 않은 NN은 아래 사진의 식과 같이 표현할 수 있다.
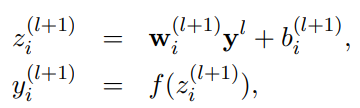
는 임의의 activation function을 뜻하고, 는 input, 는 output, 는 bias, 는 weight를 의미한다. 여기에 dropout을 추가하면, 이라는 벡터가 하나 추가된다.
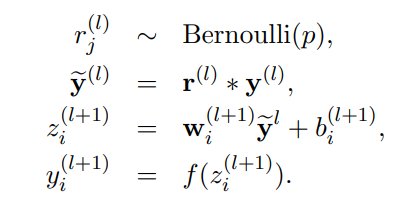
Bernoulli random variable인 는 0,1만을 값으로 갖는데, 의 확률로 1의 값을 갖고, 0일 경우 의 확률을 갖는다. 이전 layer에서 나온 output(즉 현재 layer의 input)에 이 vector를 곱해주어 thinned output인 를 얻게 되는 것이다. 나머지의 과정은 standard NN과 동일하다.
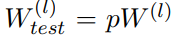
위에서 언급했던 것처럼, test time 시에 training때 얻은 weight에 를 곱해주어 output의 scale을 맞춰주는 과정도 잊지 말아야 한다.
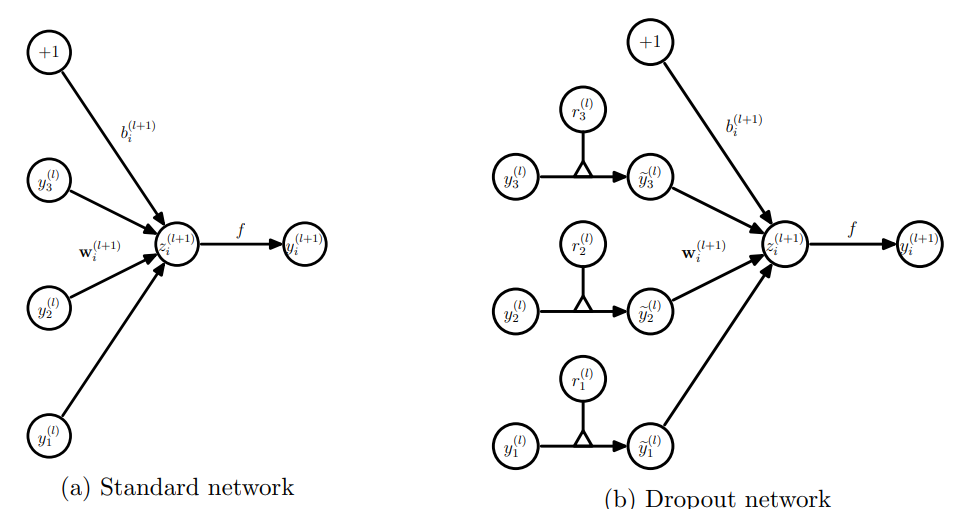
지금까지 설명했던 내용을 위 사진이 직관적으로 담고 있다.
4) Learning Dropout Nets
Dropout network들도 일반적인 NN과 동일하게 SGD를 이용해 훈련할 수 있다. 일반적인 NN과 다른 점은 각 training case마다 thinned network를 sampling해서 사용한다는 점이다. Dropout net의 forward/ backward pass는 모두 이 thinned network에서 진행된다. 일반적인 NN에서도 유용하다고 밝혀진 momentum이나 L2 weight decay 같은 방법들이 dropout net에서도 유용하다는 것도 확인할 수 있었다. 그 중에서 특히 더 효과적이었던 방법은 max norm regularization이다. weight vector의 norm이 일정 상수 c 이상 넘어가면 그 weight vector의 norm을 c로 처리하는 방법이다. norm의 upper bound를 c로 설정한 것이라고 생각하면 된다. c는 hyperparameter이고, validation set을 통해 정해진다. Dropout을 max norm regularization, large decaying lr, 높은 momentum과 함께 사용하면 그냥 dropout을 사용하는 것보다 훨씬 좋은 성능을 낸다. norm의 upper bound가 정해졌기 때문에, 최적의 weight를 찾기 위한 weight space영역도 정해진다. 그렇기 때문에 더 정교한 optimization이 가능해지는 것이다.
5) Experimental Results
저자는 다양한 분야의 classification dataset에 dropout을 적용해 보았고, 모든 dataset에서 향상된 generalization performance를 얻을 수 있었다고 한다. (MNIST, TIMIT, CIFAR-10, CIFAR-100, SVHN, ImageNet, Reuters-RCV1 등)
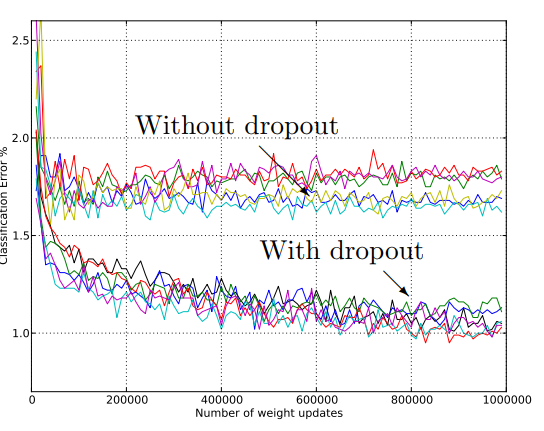
위의 그래프에서처럼, dropout을 사용할 경우, 대부분의 network들에서 test error rate가 줄어들며 성능 개선이 나타나는 것을 확인할 수 있다. 그렇다면 다른 regulariation method와 비교했을 때 dropout은 얼마나 좋은 성능을 낼까? 이 실험에서 architecture는 (784-1024-1024-2048-10)의 형태로 고정시켜 놓고, ReLU를 사용했다.

그 결과, dropout과 max-norm을 사용한 network가 1.05%의 test error rate로 가장 좋은 성능을 보였다.
6) Salient Features
지금까지 dropout이 NN의 성능을 높이는데 효과적이라는 주장을 뒷받침하는 증거들을 살펴봤다. 이번에는 dropout network의 feature들과 standard NN의 feature들을 비교해보자.
i) Effect on Features

standard NN은 다른 unit들의 영향을 받으며 weight update가 진행되기 때문에, unit들끼리 서로의 실수를 고쳐주는 현상이 나타날 수 있다. 이러한 현상은 복잡한 co-adaptation을 야기할 수도 있다. 결과적으로 co-adaptation은 보지 못한 데이터에 약하기 때문에 overfitting으로 이어진다. Dropout을 이용하면 co-adaptation을 방지하고 각 hidden unit들이 스스로 유의미한 feature를 배울 수 있게 된다. 실제로 하나의 hidden layer의 first level feature들을 출력해보면, 위의 사진과 같이 나온다. dropout을 사용하지 않는 경우, 각 feature들은 그렇게 의미 있는 것을 배우는 것 같진 않다. 반면 dropout을 사용하는 경우, feature들은 edge나 점을 찾는 것 같아 보인다. 이렇게 dropout은 co-adaptation을 방지하는 효과를 가지고 있다.
ii) Effect on Sparsity
Dropout을 적용하면서 나타나는 또 하나의 현상은 sparsity가 증가한다는 것이다. hidden unit들의 activaiton이 sparse해진다(0에 가깝거나 0이 된다)는 뜻이다. 좋은 sparse model은 소수의 highly activated unit들만 있고, 어떤 unit이던지 average activation이 낮아야 한다. 소수의 highly activated unit들은 essential한 parameter라고도 생각해볼 수 있다. 이러한 관점에서 각 network의 activation histogram을 살펴보자.
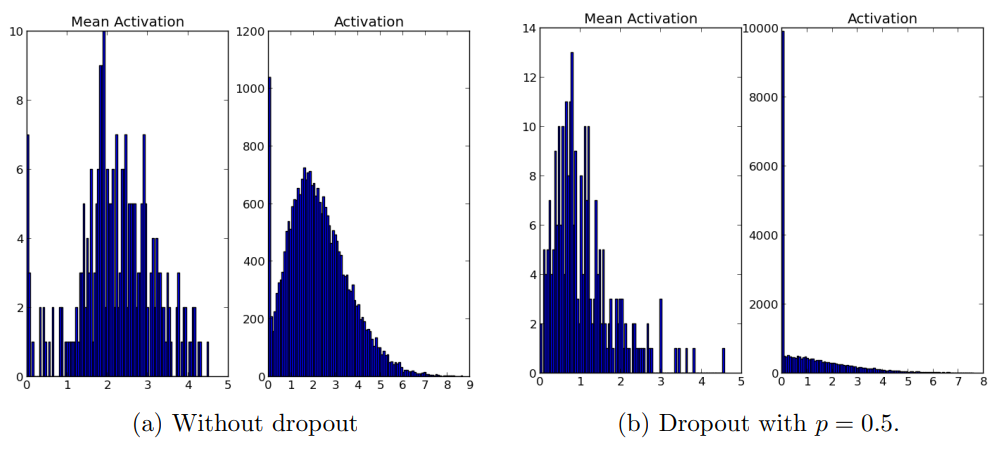
dropout을 사용하는 network가 사용하지 않는 network에 비해 high activation의 개수가 현저히 적은 것과 mean activation 또한 작은 것을 볼 수 있다.
iii) Effect of Dropout Rate
이번엔 dropout rate, 즉 에 대한 실험이다. 는 unit이 retain될 확률을 의미한다. 정확한 비교를 위해 2개의 상황을 살펴본다. 첫 번째 상황은 hidden unit들의 개수인 의 크기가 일정하게 유지되는 상황, 두 번째 상황은 이 유지되는 상황이다. 이 유지된다는 것은 thinned network의 hidden unit 개수가 일정하다는 뜻으로 해석할 수 있다.
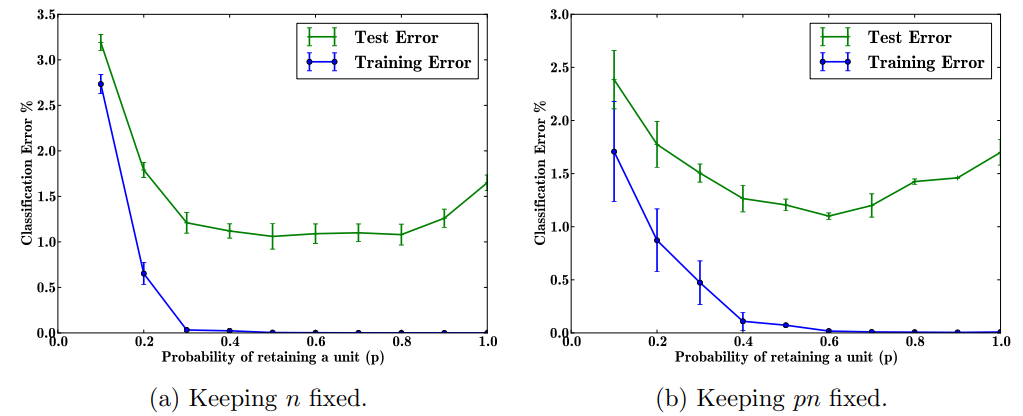
첫 번째 상황(a)의 경우, 똑같은 network architecture를 유지하고 dropout rate만 다르게 해서 실험을 진행했다. 가 증가할수록 test error는 줄어드는 경향성을 보였으나, 가 0.4와 0.8 사이일 때는 비슷한 error rate를 보였다. 그리고 가 그 이상으로 커질 때는 다시 test error가 커졌다. 두 번째 상황(b)의 경우는 초반 2개의 hidden layer의 이 되고 마지막 hidden layer의 이 되도록 세팅했다. (a)와 비교했을 때 크기가 작은 들에서 error rate가 작아진 것을 볼 수 있다. 일때 가장 좋은 성능을 보이지만, 실제로 사용할 때는 로 놓는다고 한다.
iv) Effect on Data Set Size
이번 section에서는 dataset size에 따라 error rate가 어떻게 변하는지, 즉 dataset이 얼마나 커야 dropout을 사용했을 때 효과를 얻을 수 있는지에 대한 실험을 진행한다. input layer는 , hidden layer들은 로 고정하고, 똑같은 구조의 network를 사용한다고 가정한다.
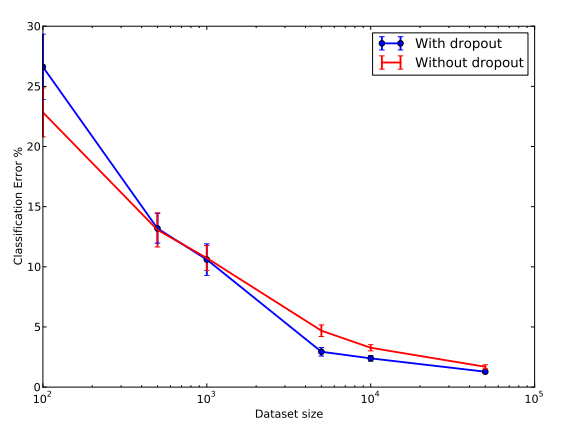
dataset의 크기가 100~500 정도일 때는 dropout을 사용하는 것이 성능 면에서 좋아지지 않는 것을 실험 결과를 통해 확인할 수 있다. dataset이 1000이 넘어가야 유의미한 성능 개선을 볼 수 있다. 또 dataset이 너무 커지면 그 전만큼 성능 개선의 폭이 크지 않다. 이는 dataset의 크기가 큰 경우 overfitting의 위험이 애초에 적어서라고 논문은 설명한다.
v) Monte-Carlo Model Averaging vs Weight scaling
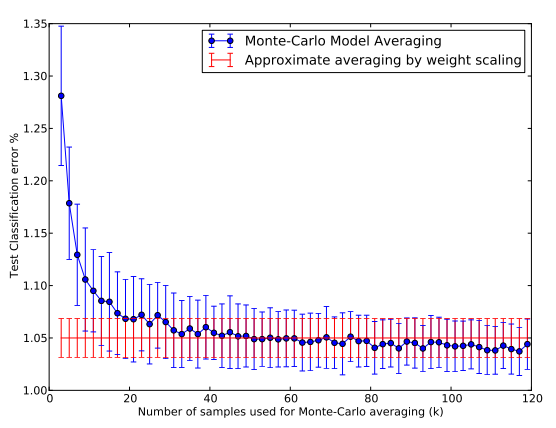
논문에서 제안하는 효율적인 test time procedure는 weight들을 scale down하여 model combination을 approximate하는 방법이다. expensive한 원래의 model averaging 방법은 각 test case별로 dropout을 적용한 k개의 NN을 sampling하여 그들의 평균을 내는 방식이다. 이를 Monte-Carlo Model Averaging이라고 하는데, k가 무한대를 향해 갈수록 이 평균이 실제 모델의 average에 가까워진다. 또, k가 커질수록 weight scaling을 통한 approximate averaging 방법의 error가 monte-carlo averaging의 error와 비슷해지는 것을 확인할 수 있다.
정리하자면, k가 충분히 커지면 true model average에 가까워지는 monte-carlo averaging과 weight scaling을 통한 approximate averaging의 error가 비슷하니, 논문에서 제안한 weight scaling 방법이 효과적이라는 것이다.
유사하게, RBM에서도 dropout은 좋은 성능을 낸다.
3. 논문 내용의 실용성
Dropout은 굉장히 많이 쓰이는 method이다. CNN을 비롯한 많은 네트워크에서 효과적이라고 받아들여지는 만큼, 내가 문제를 해결할 때 사용할 수 있는 중요한 테크닉이다. Overfitting을 방지하는 효과가 있다는 점에서 일종의 regularizer로도 생각할 수 있다. 인공지능을 할 때 반드시 알고 있어야 할 regularization 방법 중 하나인 것 같다.
4. 찾아볼 레퍼런스
1) Hinton et al., 2007, "Restricted Boltzmann Machines for Collaborative Filtering"
2) Hinton et al., 2006, " A Fast Learning Algorithm for Deep Belief Nets"
3) R.M. Neal, Bayesian Learning for Neural Networks, Lecture Notes in Statistics No.118 - Markov chain Monte Carlo method
마지막의 'Marginalizing Dropout' 부분은 수학적인 부분이 많아서 거의 이해하지 못했다. 추후에 내용을 이해해보려고 시도할 생각이다. Boltzmann Machinne과 Restricted Boltzmann Machine에 대한 이해도 부족하기 때문에 관련 내용을 찾아봐야 한다. 이외에 Marchov chain과 Monte Carlo Method도 논문을 읽다보면 자주 등장하는 내용이기 때문에 꼭 짚고 넘어가야 한다.
