최적화 (Optimization)

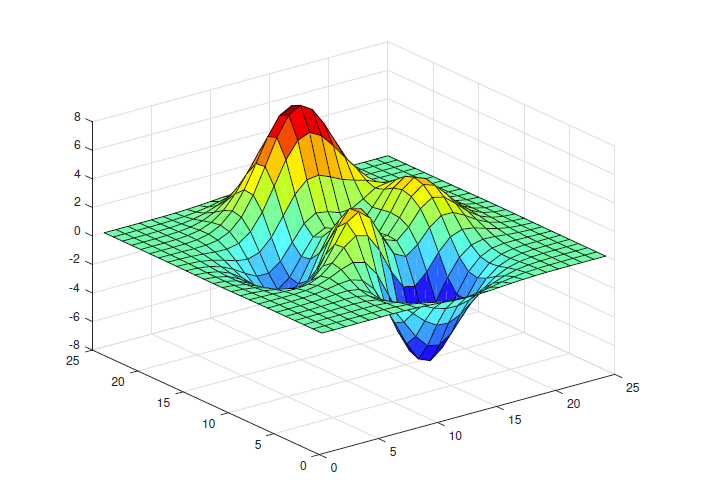
실수값, 함수, 정수에 대해 그 값이 최대나 최소가 되는 상태를 해석하는 문제.

Deep Learning 측면에서 해석하자면, Loss Function의 최소값을 찾아나가는 일련의 과정.

최적화는 Backpropagation을 통해 Weight를 업데이트하며 진행한다.

이 때 Backpropagation을 어떻게 할 것인지(얼마나 많이 움직일까? 어떤 방향으로 움직일까?)에 대해 여러가지 방법론들이 존재하며, 다음과 같다.

1. SGD

SGD, mini-batch GD, Batch GD의 차이를 친절히 설명해준 영상

손실함수의 최소값을 찾는 데에는 앞서 봤던 Gradient Descent 방법이 사용된다.

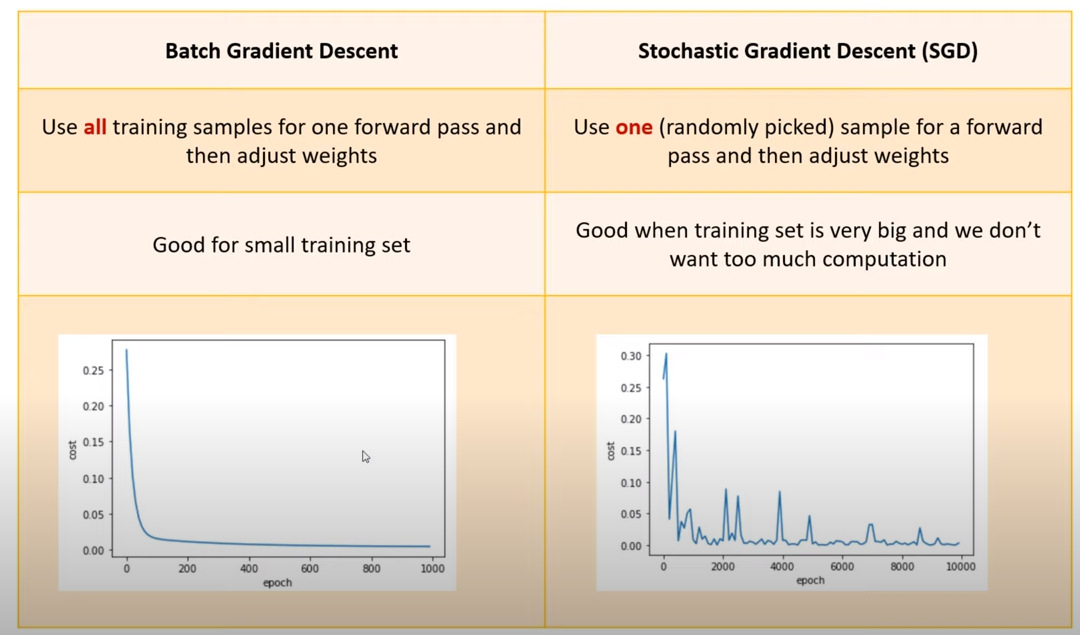
Batch Gradient Descent

한번 학습할 때 모든 데이터를 가지고 연산을 진행한다.
연산량이 많아서 느리다.

Mini-Batch Gradient Descent

한번 학습할 때 데이터 중 sunsampling을 진행하여 subset of data로 연산을 진행한다.
학습이 빠르게 이뤄지지만, Error rate를 그래프로 찍어보면 불안정하게 진행된다.
돌려보면 이해된다

Stochastic Gradient Descent

한번에 전체 데이터 중 하나만 랜덤으로 뽑아 학습을 진행한다.
불안정하다.

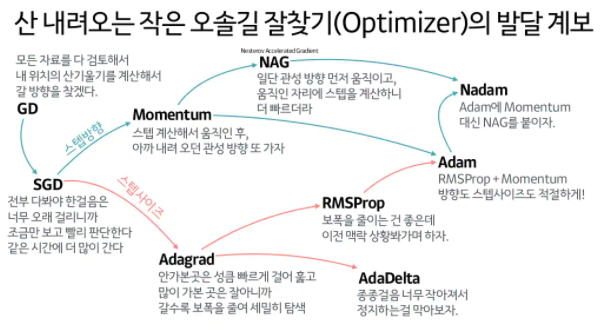
이런 옵티마이저들의 문제를 해결하기 위해 아래의 Optimizer들이 등장!

2. Momentum

3. NAG (Nesterov Accelerated Gradient)

4. Adagrad

5. Adadelta

6. RMSprop

7. Adam

참조
옵티마이저 정복
딥러닝 뇌에 박기 PPT
SGD, 옵티마이저 코드와 함께 설명
An overview of gd optimization algorithms