Kernel PCA

커널 주성분분석Kernel PCA

PCA

주성분분석(Principal Component Analysis, 이하 PCA) 의 기본원리는 Input Matrix의 고유값을 이용해 Input 데이터들의 성분을 분리하는 것이다.

원리

Input Matrix $\mathbf{X}$가 p개의 성분과 첫 열로 일벡터를 가지는 n개의 데이터셋, 즉 $n\times (p+1)$ 행렬이라고 하자. 즉,

로 두면, 다음과 같은 $n\times p$ 중심화행렬

을 만들 수 있다. 이때 행렬 $\mathbf{X_{1,\perp}}^\top\mathbf{X_{1,\perp}}$ 이 Positive Definite 이므로, 고유값분해를 이용해

로 표현가능하다. 이때 $p\times p$ 행렬 $\Lambda$ 는 고유값들로 이루어진 대각행렬 $diag(\lambda_i)$ 이다. 만약 고유값들을 크기가 큰 순부터 정리하여 $\lambda_1\geq\cdots\geq\lambda_p$ 가 되도록 한다면, 처음 $k(<p)$ 개의 고유값을 선택하고 이에 대응하는 고유벡터들을 $\mathbf{P}$ 에서 취하면 이를 주성분분석이라 한다. $j$번째 고유값에 대응하는 고유벡터를 $\mathbf{v_j}=(v_{j1},\ldots,v_{jp})$ 라고 했을 때, 새로운 벡터 $\mathbf{z_j=X_{1,\perp}v_j}$ 를 정의하면 이는 새로운 input 벡터로 볼 수 있고 이를 각각의 주성분이라고 한다.

PCA의 최적화적 관점

앞서 행렬의 분해로 설명한 PCA를 최적화 문제로 끌고와보도록 하자. 쉽게 설명하기 위해 Input Space를 $\mathbb{R^p}=\mathbf{X}$ 로 하고 여기서의 유한데이터셋 $S=(\mathbf{x_1,\ldots,x_n})$ 이 중심화벡터라고 하자 (원소들의 합이 0). $\mathbf{X}$의 각 원소에 대한 $w\in \mathbb{R^p}$ 방향으로의 정사영을 $h_w:\mathbf{X}\to\mathbb{R}$ 로 두면 이를

로 표현할 수 있다 (정사영의 정의). 이때, PCA는 $w_1,\ldots,w_p$로 연속적인 축(axis)을 찾는 것이라고 할 수 있는데, 각각의 $w_i$는 나머지 축들과 직교한다. 여기에서 최적화 문제가 발생하는데, 효과적인 축을 찾기 위해 정사영 $h_w$의 분산을 최대화해야 한다는 것이다.

또한, 이렇게 정의된 분산을 empirical variance라고 한다.

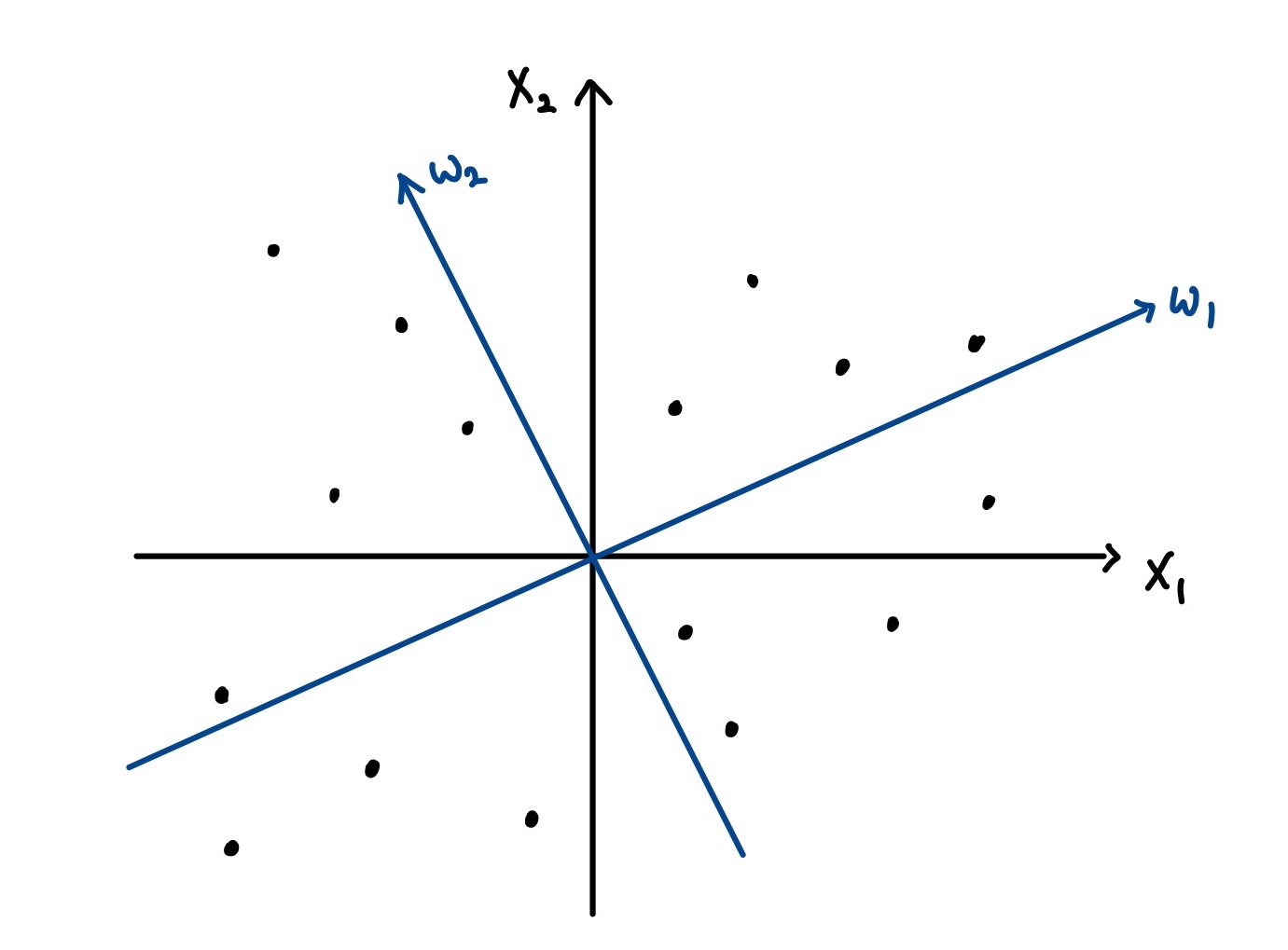
Input Data가 두개의 성분 x1,x2를 가질 떄 PCA는 분산을 최대화하는 두 축 $w_1,w_2$(파란색) 를 찾는 것이다.
이렇게 설명되는 PCA와 앞서 설명한 행렬의 고유값분해를 이용한 정의가 동치임은 아래에서 선형커널을 이용해 설명할 수 있다.

범함수의 최적화적 관점

이제 PCA를 범함수의 최적화 관점에서 살펴보자. 선형커널 $k_L(\mathbf{x,x'})=\mathbf{x^\top x'}$ 을 생각하고 이에 대응되는 RKHS재생커널힐베르트공간 $\mathcal{H_k}$ 가 주어진다고 해보자. PCA에서의 축 $w\in\mathbb{R^p}$ 에 대해 RKHS의 함수 $f_w\in \mathcal{H_k}$ 를 다음과 같이 정의하자.

그러면 위에서 살펴본 empirical variance는 다음과 같이 표현된다.

이떄 각각의 축 $w_i,w_j$ 가 직교하는 조건이 존재하므로, 각각에 대응하는 RKHS의 함수 $f_{w_i},f_{w_j}$ 역시 RKHS상의 점곱에 대해 직교한다. 따라서, 선형커널을 이용한 PCA(Linear PCA)는 다음 최적화 문제로 귀결된다.

PCA as functional optimization
선형PCA는 $f_i:i=1...p$ 를 차례대로 찾는 문제로, 다음 범함수 $\Psi$ 를 최대화시킴과 동시에 $f_1...f_{i-1}$ 까지의 함수들과 직교해야한다.

$\forall f\in\mathcal{H_k},\quad \Psi(f)=\frac{1}{n\Vert f\Vert^2}\sum_{j=1}^nf(\mathbf{x_j})^2$

표현자 정리의 적용

앞선 최적화 문제

는 표현자정리의 조건을 만족시킨다(범함수 $\Psi$ 가 $\Vert f\Vert$에 대해 단조감소하므로). 그러므로 표현자정리를 적용하면 우리는 위 최적화 문제, 즉 선형PCA의 해가 되는 함수들이 다음의 형태를 취함을 알 수 있다.

이떄 각 $i$에 대해 $(\alpha_{i,1},\ldots,\alpha_{i,n})^\top\in\mathbb{R^n}$ 이고 이를 $\alpha_i\in\mathbb{R^n}$ 으로 정의하자. 그러면 각 함수의 노음은 다음과 같이 표현된다.

또한, 이를 이용하여 최적화 문제를 다시 쓰면 PCA는 결과적으로 연속적인 벡터 $\alpha_1,...\alpha_p\in \mathbb{R^n}$ 이 $\alpha_i^\top K\alpha_j=0$ 인 제약조건 하에서 (행렬 $K$는 커널 행렬 $(K)_{ij}=k(\mathbf{x_i,x_j})$ 를 의미한다)

의 값을 최대화시키도록 하는 것이다. 이때 커널행렬은 positive definite하므로 $K^{1/2}$가 존재한다. $\beta=\alpha^\top K^{1/2}$ 로 두면 최적화는

으로 쓸 수 있다. 위 최적화 문제는 Rayleigh's quotient 형태이므로, 커널행렬 $K$의 가장 큰 고유값에서 최대가 된다. 따라서 이 문제는 가장 큰 값부터 순차적으로 고유값을 찾아가는 문제이므로 이는 위 PCA에서 살펴본 고유값분해 문제와 동치이다.

비선형커널을 이용한 PCA

비선형커널 PCA의 대략적인 원리를 설명하는 다음 그림을 살펴보자.

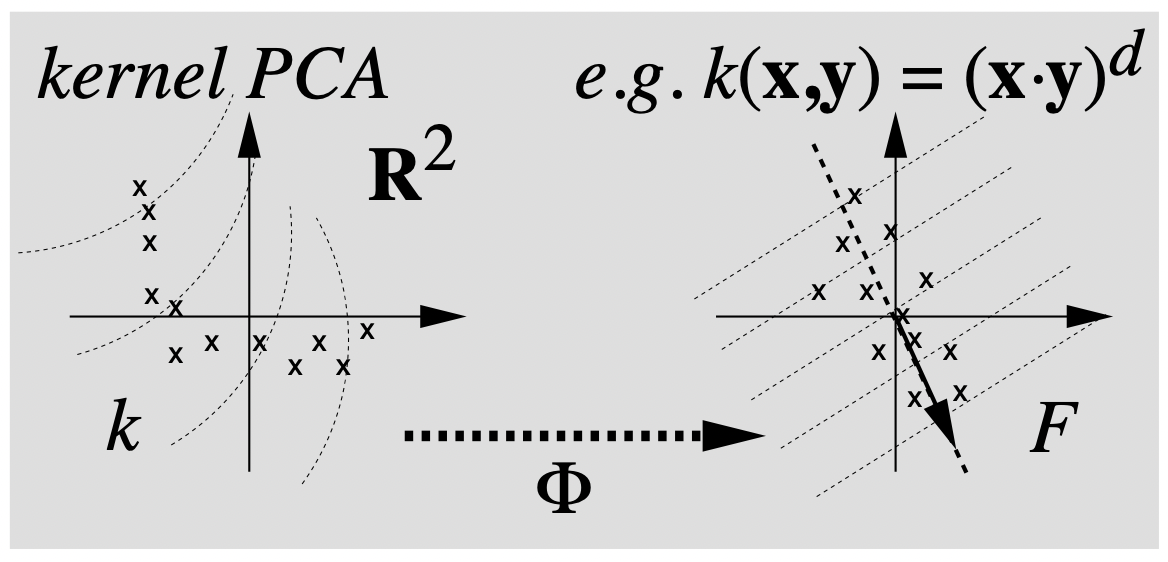
왼쪽과 오른쪽 그림 모두 두개의 성분을 가지는 $\mathbb{R^2}$ 상의 데이터셋을 표현한 것이다. 이떄 특성공간 $\mathcal{F}$ 로의 사상 $\Phi:\mathbb{R^2}\to \mathcal{F}$ 가 주어진다고 하자. 오른쪽 그림은 각 데이터를(x로 표시된 점들) 특성함수로 mapping해서 Linear PCA를 실행시킨 것이다. 이떄 오른쪽 그림의 대각 화살표는 주성분을 나타내고, 이와 수직으로 그려진 점선들은 주성분의 등고선을 의미한다. 반면, 왼쪽 그림은 다항커널($(\mathbf{x,y})^d$)과 같은 비선형커널을 이용해 커널행렬을 구하고 PCA를 진행한 결과이다. 오른쪽 그림의 직선형태인 등고선은 왼쪽에서 비선형으로 나타남을 확인할 수 있으며, 고유벡터의 존재성 역시 확실하지 않기 때문에 주성분이 표시되지 않음을 의미한다.
핵심은, 이미지, 영상과 같은 고차원 대용량 데이터를 처리하게 될 경우 오른쪽과 같이 특성공간으로 매핑하게 된다면 계산 비용이 과도해지는 문제가 발생하게 될 수 있다는 것이다. 이때 커널함수를 이용한다면 커널행렬을 구하는 연산만으로도 주성분 분석을 쉽게 할 수 있다. 이는 계산비용을 효과적으로 사용할 수 있게 해준다.

References

• A primer on kernel methods, J.Philippe Vert et al.
• Linear Models in Statistics
• Nonlinear Component Analysis as a Kernel Eigenvalue Problem, B.Scholkopf et al. 1998