LDA (2)

LDA의 다른 관점
이전 포스트에서 살펴본 것 처럼, LDA는 데이터셋의 정규성을 가정하여 분류하는 방법이다. 이를 제한된 가우시안 분류기restricted gaussian classifier라는 관점으로 본다면, 이번에 다룰 내용은 LDA가 데이터를 저차원으로 투영시켜 본다는 정사영projection의 관점이다.

클래스가 $K$개인 데이터셋이 있고, 각각의 데이터는 $p$개의 변수를 갖는 상황을 생각하자. 이떄 각 클래스에 대한 무게중심점(평균)centroid 을 구할 수 있는데, 이때 $K$개의 중심점은 $p$차원 공간의 원소이다. 그런데 $K$개의 중심점을 모두 포함하는 초평면을 생각한다면, 이는 아핀 부분공간affine subspace 이므로 $K-1$ 차원의 공간을 형성한다. 만일 $p$가 $K$보다 충분한 정도로 크다면, 차원축소dimensionality reduction가 일어나는 상황으로 볼 수 있다.

Dimensionality Reduction

차원 문제는 머신러닝에서 중요하게 풀어야 할 숙제이다. 데이터셋의 차원이 증가할수록 신뢰할만한 모형을 얻기 위해 필요한 데이터의 양($N$)이 기하급수적으로 증가한다. 이처럼 고차원에서 발생하는 문제들을 차원의 저주curse of dimensionality라 하는데, 이를 해결하기 위해서 다양한 차원축소 방법이 존재한다. 이전 다른 포스팅에서 살펴본 PCA 가 대표적인 예시이다. 그렇다면 선형분류기인 LDA가 어떻게 차원축소의 기능을 하는지 살펴보도록 하자.

Fisher's Idea

Fisher는 LDA의 최적화 문제를 계산하는 과정에서 다른 아이디어를 제시했다. 이전 포스트에선 LDA가 정규성 가정, 즉 데이터셋이 정규분포를 만족한다는 가정으로부터 얻어진다고 설명했다. 하지만 실질적으로 최적화 문제를 해결하는 과정에서 정규성가정과는 무관하게 답을 찾을 수 있다.

차원축소를 시행하면 PCA와 같이 주성분들을 얻을 수 있다. 이때 주성분은 데이터셋 $X$의 열공간들의 선형결합을 의미하므로 이를 $Z=a^\top X$라고 두자. 우리가 찾아야하는 것은 $Z$에 대해 어떤 최적화 문제를 풀어야 하는지인데, 그림으로 파악해보도록 하자.

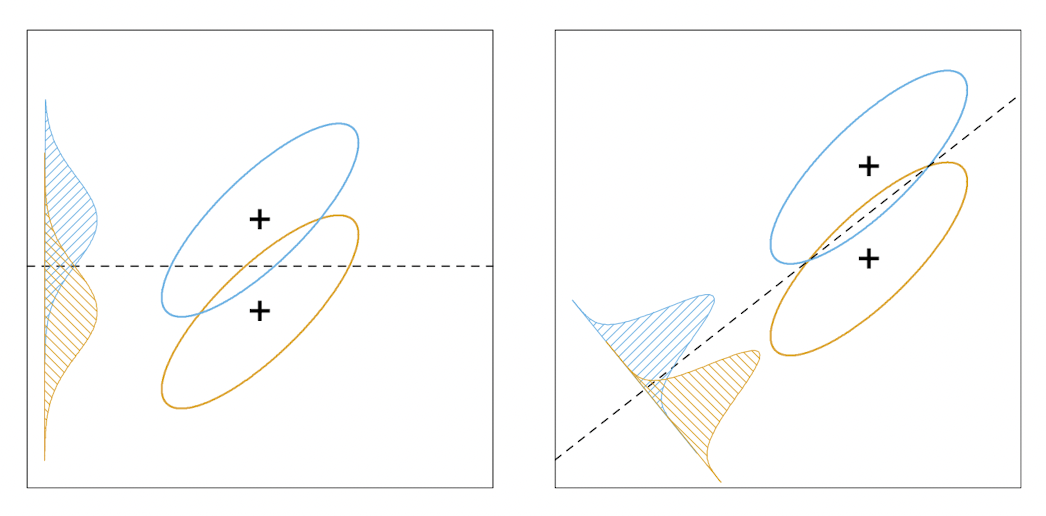
위 그림에서 왼쪽과 오른쪽을 비교해보도록 하자. 두 개의 십자 표시는 각 클래스들의 중심 centroid를 의미하고, 각 색상으로 두 클래스들의 분포를 보여주고 있다. 각 그림에서 점선은 discriminant line을 의미하는데, 왼쪽 그림에서의 클래스 분류가 클래스 간between-class 분산을 더 크게 만드는 것을 확인할 수 있다. 그러나 데이터들을 y축으로 정사영시키면 중첩되는 부분이 더 큰데, 이는 클래스 내within-class 분산으로 인해 발생하는 것이다. 따라서 더 합리적이고 효과적인 결정경계를 찾기 위해서는 클래스내 분산 역시 고려해야한다.

$Z$의 분산은 이차형식으로 나타나므로, 클래스간 분산은 $a^\top\mathbf{B}a$, 클래스내 분산은 $a^\top\mathbf{W}a$ 로 나타내자. 이때 $\mathbf{B+W=T}$ 이고 $\mathbf{T}$는 $X$의 클래스를 무시한 총(공)분산행렬(total covariance matrix)이다.
Fisher는 클래스내 분산을 최소화하여 데이터간 중첩을 최소화하고, 클래스간 분산을 최대화하는 최적화 문제가 LDA로 치환된다는 것을 설명했다. 즉, 다음의 라일라이 몫Rayleigh quotient 형태의 최적화문제

를 해결하는 것이다. 이때 라일라이 몫의 최대값은 행렬 $\mathbf{W^{-1}B}$ 의 최대 고유값과 같음이 알려져있으므로 우리는 LDA 문제가 결국 고유값문제로 치환됨을 알 수 있다.
따라서 위 문제의 해를 $a_1$ 이라 할 떄 LDA를 통해 분리한 첫번째 차원(주성분)은 $Z_1=a_1^\top X$가 된다. PCA와 마찬가지로 $a_1$과 $\mathbf{W}$에서 직교하는 성분 $a_2$을 찾을 수 있고, 계속해서 $a_l$을 찾아나갈 수 있다.

Reference

• Elements of Statistical Learning