Markov Chain Monte Carlo
MCMC라고도 하는 Markov Chain Monte Carlo 기법은 확률분포에서 샘플을 추출하는 여러 종류의 알고리즘을 일컫는다. 다양한 머신러닝 이론들이 등장하며, 기존 통계학에서 다룰 수 없을 정도의 수만-수백만 개의 변수 및 파라미터를 사용하는 모델들 역시 등장했고, 특히 신경망과 같은 모델들은 너무나도 널리 사용되고 있다. 하지만 그러한 고차원 모델들에 대해 샘플링을 수행하거나, 기댓값 등 적분값을 구하는 과정은 기존의 다중적분으로는 불가능하다. 이를 해결하기 위해 몬테카를로 방법, 그중에서도 마코프 체인을 이용한 MCMC가 사용되며 이는 근래 통계학 및 머신러닝 분야에서 매우 중요한 부분을 차지한다.
Markov Chain
Markov Chain은 시간()에 따라 변화하는 시스템(계)의 상태를 설명하기 위한 개념이다. 어떤 시스템의 상태가 A에서 B로, B에서 C로 시간()에 따라 변화하는 과정이 각각 확률로 주어지는 것을 의미한다. 만일 시간 에서의 상태를 모두 포함하는 충분통계량 가 존재하며, 모든 과거의 상태가 이에 포함된다면 이를 markov property라고 한다. 즉, 다음을 의미한다.
Markov property가 만족될 경우 유한한 확률과정열을 다음과 같이 쓸 수 있는데,
이를 Markov Chain 이라고 한다.
Stationary Markov Chain
다음과 같이 time-shift가 이루어져도 joint distribution이 일치하는 markov chain을 stationary markov chain이라고 한다.(stationary : 정상성)
또한 stationary markov chain에서의 marginal distribution, 즉 을 해당 마코프 체인의 stationary distribution이라고 한다.
Monte Carlo Integration
몬테카를로 적분은 확률변수의 기댓값, 즉 적분값을 random sampling으로 근사하는 방법이다.
확률변수 와 target distribution 에 대해 기댓값을 구하기 위해서는 위와 같은 적분을 계산해야 한다. 그러나, 때로는 적분의 closed form을 구하기 어렵거나 데이터가 고차원인 경우 계산 과정이 매우 복잡하여 computation cost 문제가 발생할 수 있다. 이를 극복하기 위해 다음과 같이 적분값을 근사하는 방법을 Monte Carlo integration이라고 한다.
MCMC
Markov Chin Monte Carlo(이하 MCMC)는 몬테카를로 방법 중에서 가장 널리 사용되는 기법 중 하나이다. MCMC의 기본적인 아이디어는 상태공간 에서 target density 를 stationary distribution으로 하는 마코프 체인을 구성하는 것이다. 이는 상태공간에서 각 상태 에 머문 시간()의 비율이 에 비례하도록 random walk를 진행하는 것을 의미한다.
이러한 random walk로부터 샘플 를 추출하여 확률측도 에 대해 몬테카를로 적분을 실행할 수 있다. 이때 중요한 것은, random walk의 초기 과정은 sample의 개수가 적기 때문에 이때에는 정상성(stationarity)이 보장되지 않는다. 따라서 정상성에 이르는 시간동안의 샘플은 제거하는 것이 맞으며, 정상성에 이르기까지의 시간을 burn-in time이라고도 한다.
MH(Metropolis Hastings) Algorithm
MCMC 알고리즘의 가장 대표적인 것 중 하나인 MH 알고리즘에 대해 살펴보도록 하자. 앞서 MCMC의 기본 원리는 상태간 이동이 정상분포()에 근거해 이루어진다고 설명한 바 있다. MH 알고리즘에서는 의 상태이동이 확률 로 이동하는데, 는 proposal distribution 이라고 한다(새로운 상태 로 움직일 것을 제안받는다는 의미로 proposal이라고 하는 것 같다😃).
알고리즘에서 로의 상태 이동을 제안받으면, 그 제안을 accept 할 것인지 결정하는 과정이 존재한다. Accept가 이루어지면 를 새로운 샘플로 사용하고, 그렇지 않으면 기존 샘플을 반복해서 추출한다. 전체 알고리즘은 다음과 같다.
Metropolis Hastings Algorithm
Initialize
각 단계 에 대해 다음 과정을 반복한다:
- 으로부터 새로운 샘플을 추출한다.
- Acceptance probability를 계산한다.
- 으로부터 샘플을 추출한다.
- 새로운 샘플 을 다음과 같이 정의한다.
여기서 로 는 정규화되지 않은 분포를, 는 정규화상수를 이용하여 정규화된 분포를 각각 나타낸다.
MH 알고리즘이 실제로 정상확률분포 로부터 샘플을 생성한다는 것을 증명하는 자세한 과정은 참고 교재를 살펴보면 좋을 것 같다. 아래는 실제로 MH 알고리즘을 이용한 sample generating을 코딩해보도록 하겠다.
Code
앞서 살펴본 MH 알고리즘에서, proposal distribution을 simple normal distribution 로 하는 코드를 구현해보도록 하자. 필요한 패키지들은 다음과 같다.
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt샘플링하고자 할 타겟 분포를 이번에는 평균이 5, 표준편차가 10인 정규분포로 하고, 다음과 같이 random variable을 scipy.stats 으로 설정했다.
# Parameter
MU = 10.0
SIGMA = 5.0
target = ss.norm(loc=MU, scale=SIGMA) # target distributionMH 알고리즘은 아래와 같은 코드로 진행시켰다. 총 반복횟수는 10000회로 둔 뒤 초기값은 임의로 설정했고(3.0, random으로 생성해도 된다) 각 반복문의 단계에서 이전 state에 proposal distribution을 더한 값 x_proposed으로 값을 계산하여, uniform distribution에서 추출한 와 비교한 뒤 새 단계의 state를 업데이트 하는 방식이다.
# Rep count = 10000
x = np.zeros(shape=10000)
# initialize x_0
x[0] = 3.0
for i in range(1,10000):
x_t = x[i-1]
x_proposed = x_t + np.random.standard_normal(1)[0] # Proposal Distribution
A = min(1, target.pdf(x_proposed) / target.pdf(x_t)) # Since q is symmetric
u = np.random.uniform(size=1)[0] # u from Uniform dist
if u <= A : # Accept
x[i] = x_proposed
else:
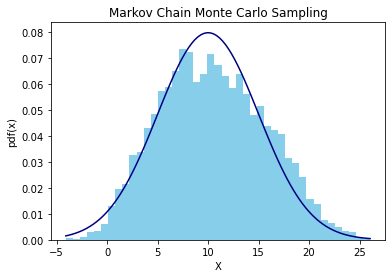
x[i] = x_tPlotting한 결과는 다음과 같다.
References
- Probabilistic Machine Learning : Advanced Topics, Murphy.
- Code at github : https://github.com/ddangchani/Velog/blob/main/Statistical%20Learning/MCMC.ipynb