Probabilistic Graphical Models

이전에 graph의 markov property을 살펴보며 markov property 하에서(parent 노드가 주어질 때 다른 노드들과의 조건부 독립성) graphical model을 다음과 같은 markov chain 형태로 나타낼 수 있음을 알았다.

만일 각 노드가 discrete random variable로 주어진다면, 각 노드에서의 조건부 확률분포(CPD, conditional probability distribution)를 table 형태로 표현할 수 있다. i번째 노드에서의 conditional probability table(CPT)은 다음과 같이 주어진다.

여기서 $k, j$는 각 노드의 상태(이산값)를 의미하며, 따라서 전체 그래프 모델에서의 CPT는 3D 텐서로 주어지게 된다.

Example with Python Code

교재에서 다루는 5개의 discrete random variable로 이루어진 그래프를 모델링하고 시각화하는 방법에 대해 살펴보도록 하자. Student Network 라고 부르는 이 그래프는 가상의 학생에 대해 관련된 이산변수들(D=수업 난이도, I=지능, G=성적, S=SAT 점수, L=추천문구(good/bad)) 들로 구성되어있다. 연쇄법칙에 의해 joint probability는 다음과 같이 나타난다.

Python에서는 pypgm 라이브러리를 활용해 그래피컬 모델링이 가능하다. 우선 다음과 같이 패키지들을 불러오자.

import probml_utils.pgmpy_utils as pgm
from causalgraphicalmodels import CausalGraphicalModel
import pgmpy
import numpy as np
import pandas as pd
from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD

이제, 다음과 같은 노드((x,y) 형태)들의 리스트로 BayesianNetwork의 초기 설정이 가능하다.

model = BayesianNetwork([('Diff', 'Grade'), ('Intel', 'Grade'), ('Grade', 'Letter'), ('Intel', 'SAT')])

또한, 다음과 같이 시각화할 수 있다.

# DAG
model2 = CausalGraphicalModel(nodes=model.nodes(), edges=model.edges())
dot = model2.draw()
display(dot)

설정한 네트워크의 각 노드별 조건부 확률분포(CPD)를 다음과 같은 tablular form으로 설정하여, 모델에 적용할 수 있다.

# Define Individual CPD with state name
cpd_d_sn = TabularCPD(variable="Diff", variable_card=2, values=[[0.6], [0.4]], state_names={"Diff": ["Easy", "Hard"]})
cpd_i_sn = TabularCPD(variable="Intel", variable_card=2, values=[[0.7], [0.3]], state_names={"Intel": ["Low", "High"]})
cpd_g_sn = TabularCPD(
    variable="Grade",
    variable_card=3,
    values=[[0.3, 0.05, 0.9, 0.5], [0.4, 0.25, 0.08, 0.3], [0.3, 0.7, 0.02, 0.2]],
    evidence=["Intel", "Diff"],
    evidence_card=[2, 2],
    state_names={"Grade": ["A", "B", "C"], "Intel": ["Low", "High"], "Diff": ["Easy", "Hard"]},
)

cpd_l_sn = TabularCPD(
    variable="Letter",
    variable_card=2,
    values=[[0.1, 0.4, 0.99], [0.9, 0.6, 0.01]],
    evidence=["Grade"],
    evidence_card=[3],
    state_names={"Letter": ["Bad", "Good"], "Grade": ["A", "B", "C"]},
)

cpd_s_sn = TabularCPD(
    variable="SAT",
    variable_card=2,
    values=[[0.95, 0.2], [0.05, 0.8]],
    evidence=["Intel"],
    evidence_card=[2],
    state_names={"SAT": ["Bad", "Good"], "Intel": ["Low", "High"]},
)

model.add_cpds(cpd_d_sn, cpd_i_sn, cpd_g_sn, cpd_l_sn, cpd_s_sn)
model.check_model()

또한, 마찬가지로 pgmpy_utils 모듈을 이용해 다음과 같이 시각화 할 수 있다.

# CPT
dot = pgm.visualize_model(model)
display(dot)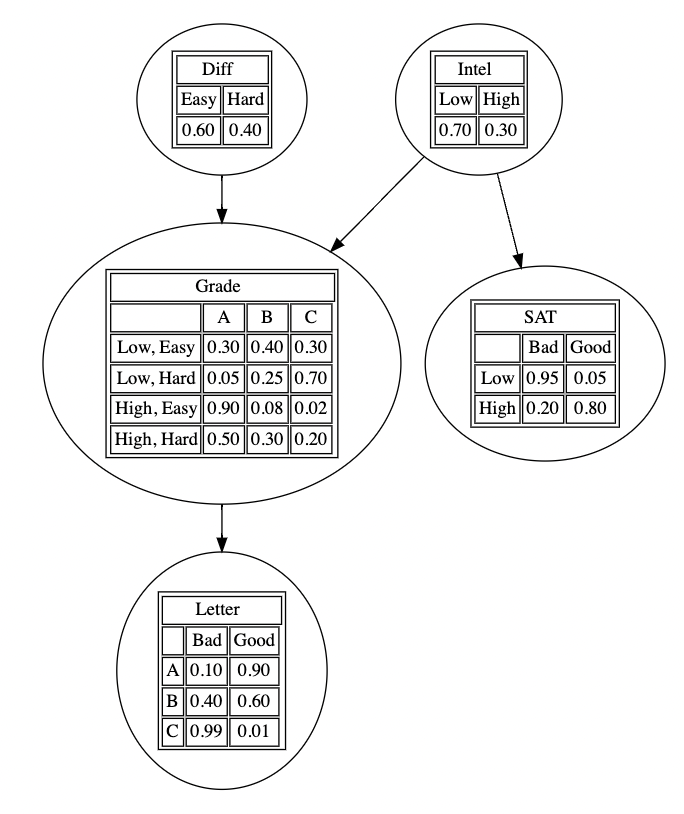

또한, 각 treatment(여기서는 Grade가 B인 경우를 예시로 선택)에 대한 다른 노드들의 marginal distribution을 확인할 수 있다. 이러한 형태의 추론을 쿼리(query)라고도 하는데, 다음과 같이 evidence를 설정하고, VariableElimination 클래스를 활용해 조건부 분포를 찾거나 혹은 get_marginals, visualize_marginals을 이용해 시각화할 수 있다.

# Inference
evidence = {'Grade' : 'B'} # posterior given grade=B
postD = infer.query(['Diff'], evidence).values
print("Pr(Difficulty=Hard|Grade=B) = {:0.2f}".format(postD[1]))

# Result : Pr(Difficulty=Hard|Grade=B) = 0.37

# Visualize
evidence = {'Grade' : 'B'}
marginals = pgm.get_marginals(model, evidence)
dot = pgm.visualize_marginals(model, evidence, marginals)
display(dot)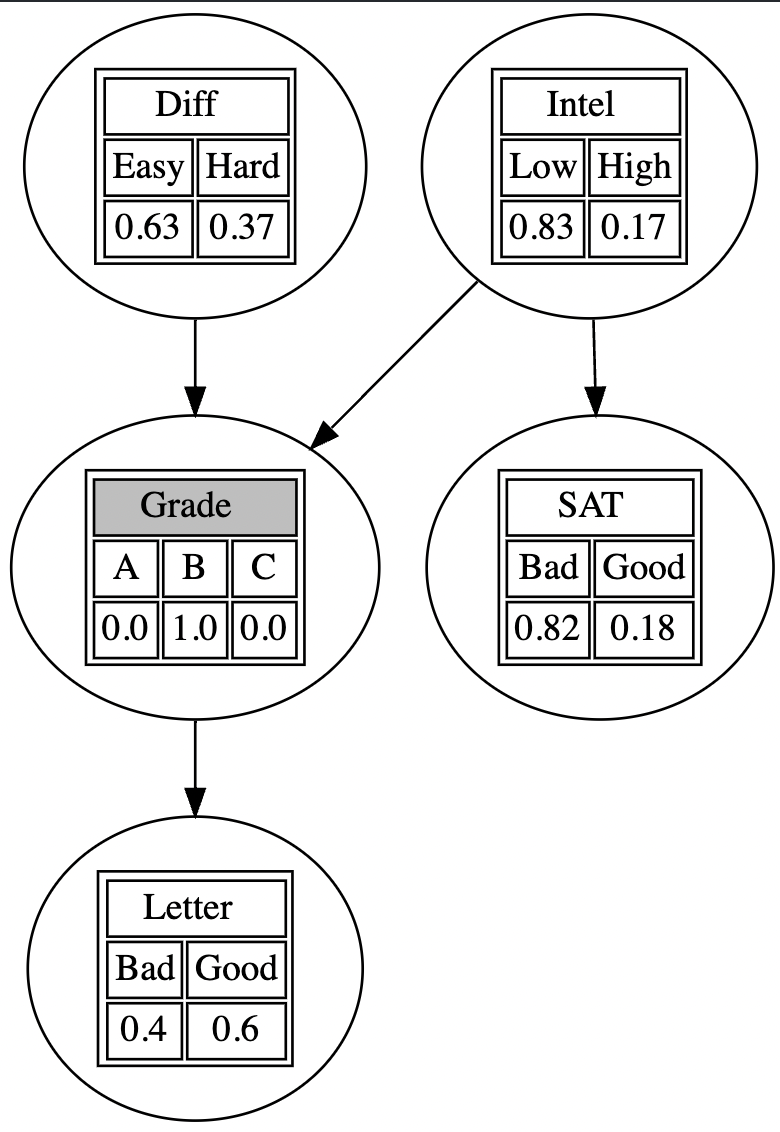

References

• Probabilistic Machine Learning - Advanced Topics
• https://colab.research.google.com/github/probml/pyprobml/blob/master/notebooks/book2/04/student_pgm.ipynb#scrollTo=8FEYdsYCXYj5