[ASR] Gaussian Mixture Model

누렁이·2024년 2월 22일
0

Speech (ASR/TTS)

목록 보기
11/15

https://hyunlee103.tistory.com/56 보고 다시 재정리
ref: https://ratsgo.github.io/speechbook/docs/am/gmm

Preview of Gaussian Mixture Model (GMM) in ASR

Review: HMM & 바움웰치

HMM의 전이 확률 (다른 상태로 전이될 확률), 방출확률분포 (특정 상태에서 관측될 수 있는 데이터 확률 분포) 파라미터 학습하는 알고리즘.

  • (1) 초기화: random하게 전이 A, 방출B 확률 초기화
  • (2) expectation step: A,B 고정 시키고, ξ크사이(t 시점에서 i, t+1일때 j일 확률), γ (t일 때 j일 확률) 구하기
  • (3) maximization step: e-step에서의 ξ, γ가지고 A,B구하기
  • (4) iteration: 수렴할 때까지 반복
    => 이때 방출확률 구하는 걸 GMM으로 함!

Introduction of HMM+GMM

  • Background:
    HMM에서 관측값이 아이스크림 개수처럼 discrete한 값이면 likelihood 계산 시 필요한 emissioin probability 계산하기 쉬움.
    그런데 mfcc는 continuous해서 딱 떨어지게 계산하는게 어려움.

  • Approach:
    So, GMM을 도입해서 방출확률 구하기

  • 핵심포인트 of GMM + HMM

    'six'라는 단어가 있을 때, 'six' word는 아래 그림처럼 하나의 HMM 모델로 구성 됌 (음소 (Phoneme) sequence (/sɪks/), states, transition probabilites들로 구성)

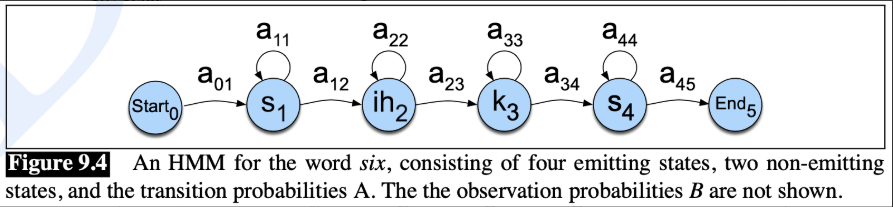
    • GMM:
      소리 특징 파악 == 특정 음소가 특성 acoustic features (e.g., mfcc)로 관측될 확률 계산
      • e.g) /s/, /ɪ/, /k/, /s/ 각각이 특정 mfcc형태랑 matching 되는지 계산
    • HMM:
      소리들 패턴 파악 == 음소 sequence가 주어졌을 때 이게 특정 word로 관측될 확률 계산.
      • e.g) /s/, /ɪ/, /k/, /s/가 'six'라는 거 파악
    • HMM+GMM:
      GMM은 각 음소별 방출확률을 구하는거로 말할 수 있음. 따라서 HMM에서 은닉 상태(음소) 개수만큼의 GMM이 필요

GMM을 이해하기 위해 선행되어야할 지식들

GMM은 M개의 서로 다른 정규분포의 가중합으로 데이터를 표현하는 모델이라서, 다변량정규분포 파라미터 추정법 아는 게 필요.
구체적인 건 뒤쪽에다가 설명해 놨고, 여기서는 키워드만 확인하겠음!

  • Univariate Normal Distribution (정규분포)

    • 정의:
      • 평균 μ, 분산 σ^2인 정규분포 N(μ,σ2)
      • 주사위의 k번째 면이 n번 나올 확률을 이항분포의 예시로 설명할 수 있고, 여기서 엄청 동전을 많이 던졌을 때의 확률분포를 가우시안 분포로 말할 수 있음.

  • Multivariate Normal Distributution (다변량 정규분포)

    • 정의:정규분포를 다차원 공간으로 확장된 분포, 즉 정규분포의 input이 확률변수라면, 다변량 정규분포는 확률 벡터

  • Maximum Liklihood Estimator (MLE)

    • 목적: 다변량 정규분포의 paremeter를 추정을 위해 MLE 사용.
    • Task (D차원 다변량 정규분포의 parameter 추정 시)
      (1) D차원 평균 벡터 μ
      (2) DxD 차원 공분산 행렬 Σ
    • Method
      • (1) log-likelihood function 구하고
      • (2) 이 함수를 최대화시키는 게 목적이므로 추정하고자 하는 parameter에 대해 각각 편미분을 해준다.

Gaussian Mixture Model (GMM)

  • Mixture model 이란?

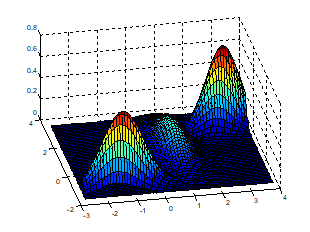
    • 데이터 히스토그램을 찍었는데 아래 그림과 같이 나왔다고 생각해보자. 정규분포 하나로 모델링 하기에는 부족해 보인다.

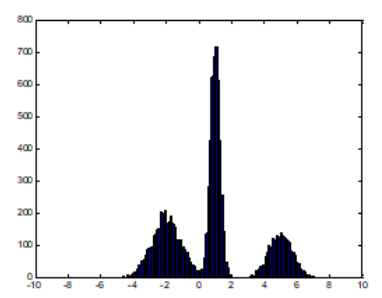
    • 그래서 서로 다른 정규분포 3개(빨강, 초록, 파랑)로부터 데이터가 나왔다고 생각해, 그 세 분포의 mixture distribution(혼합분포)으로 모델링하면 어떨까?가 Mixture Model의 기본 아이디어

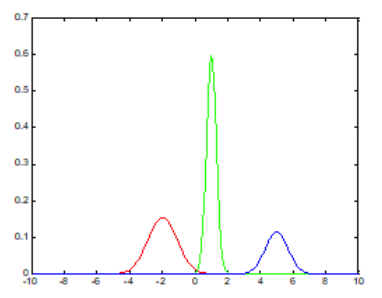
    • 그중 GMM은 혼합 분포로 쓸, 각 sub 분포들을 정규분포로 가정하고, 각 모든 sub 분포를 weighted sum해서 새로운 다항분포로 표현하는 모델

  • Gaussian Mixture model 이란?

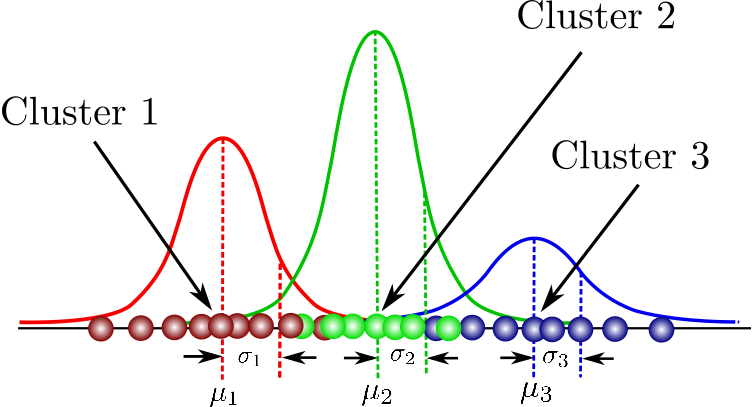
    그림: 3개의 sub 분포를 가지는 GMM

    • 개념:
      mixture model과 동일하지만 sub 분포를 정규분포로 사용하는 모델
    • 목표:
      • 데이터가 어떤 분포로 assign 될 것인가! (clustering과 유사)
      • k번째 분포에서, 주어진 데이터가 관측될 확률 구하기
    • Method:
      • (1) 모든 k번째 sub분포마다 π_k가중치 있음
      • (2) 이를 weighted sum으로 전체 GMM을 구성.
        f(X;θ)=∑k=1KπkN(x∣μk,Σk)f(\boldsymbol{X} ; \theta) = \sum_{k=1}^{K}\pi_k N(x|\boldsymbol{\mu_k}, \boldsymbol{\Sigma_k})
      • (3) Z라는 새로운 다항분포를 도입해 다음과 같이 모델링 (여기 잘 모르겠음...) 초기화를 해서 일단 그거랑 맞는지 본다는 건가..?
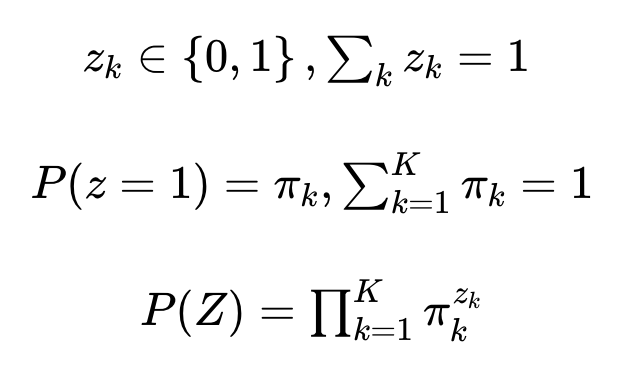
      • (4) k번째 분포에서 주어진 데이터가 관측될 확률
        f(X∣zk=1)=∏k=1KN(x∣μk,Σk)zkf(X | z_k = 1) = \prod_{k=1}^{K} N(x|\mu_k,\Sigma_k)^{z_k}
      • (5) 특정 데이터가 주어졌을 때 k번째 분포로 assign 될 assignment probability 베이즈 정리를 활용해 구하기
        γ(znk)=P(zk=1∣xn)\gamma (z_nk) = P(z_k = 1|x_n)
        =P(zk=1)P(x∣zk=1)∑j=1KP(zj=1)P(x∣zj=1)= \frac{P(z_k=1)P(x|z_k = 1)}{\sum_{j=1}^{K}P(z_j=1)P(x|z_j=1)}
        =πkN(x∣μk,Σk)∑j=1KπjN(x∣μk,Σj)= \frac{\pi_kN(x|\mu_k,\Sigma_k)}{\sum_{j=1}^{K}\pi_jN(x|\mu_k,\Sigma_j)}

GMM 학습 (Estimating GMM(E-M algorithm)

  • (1) Expectation:
    K-mean clustering에서 특정 cluster로 데이터가 assign 될 확률을 구하는 과정과 동일하다. 초기값으로는 랜덤값을 주고 학습을 시작한다. 몇개 cluster할지는 경험적으로 초기화!

  • (2) Maximization:
    expectation 단계에서 구한 assignment probability를 가지고 GMM parameter를 업데이트한다. 업데이트에 MLE를 적용하므로 log-likelihood를 각 parameter에 대해 편미분 해 MLE를 구한다.

  • (3) Iteration

    • 총 99번 E-M iteration을 돌린 GMM. 학습이 반복되면서 점점 경계에 불명확한 데이터들이 줄어들고 clustering 구조가 잡혀감.

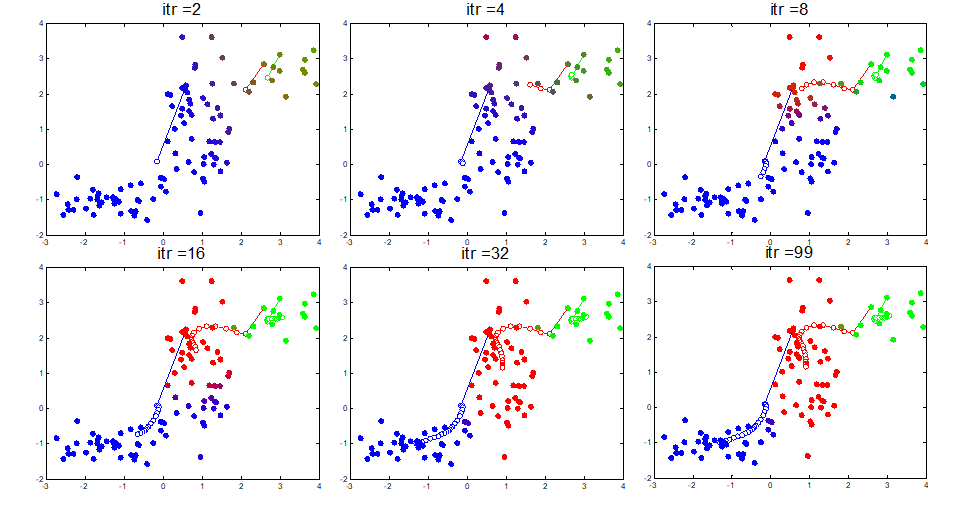
    • E-M iteration이 돌수록 log-likelihood 값이 증가해 수렴

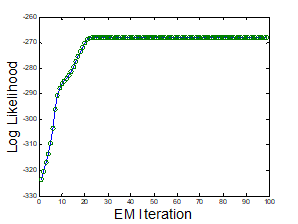
GMM for ASR 로 정리

  • HMM+GMM:
    • GMM은 각 음소별 방출확률 구하는 모델
    • HMM에서 은닉 상태(음소) 개수만큼의 GMM 필요
    • 한 state별로, 39차원 다변량 정규분포를 feature로 M개의 sub 분포 가지는 GMM으로 모델링
      bj(ot)=1(2π)D2∣Σ∣12exp⁡(−12(ot−μj)TΣj−1(ot−μj))b_j(o_t) = \frac{1}{(2\pi)^{\frac{D}{2}}\left | \Sigma \right |^{\frac{1}{2}}}\exp (-\frac{1}{2}(o_t-\mu_j)^{T}\Sigma_j^{-1}(o_t-\mu_j))

      MFCC는 39차원
      이유는 요기.. ref: https://moondol-ai.tistory.com/164

Code

GMM

https://scikit-learn.org/stable/modules/generated/sklearn.mixture.GaussianMixture.html

import librosa
import numpy as np
from sklearn.mixture import GaussianMixture
import librosa.display
import matplotlib.pyplot as plt

# 음성 파일 불러오기 
audio_path = 'your_audio_file.wav'
y, sr = librosa.load(audio_path)

# MFCC 계산
mfccs = librosa.feature.mfcc(y=y, sr=sr)

# GMM 학습
n_components = 5 # GMM 컴포넌트 수, 즉 클러스터의 수
gmm = GaussianMixture(n_components=n_components, random_state=42)
gmm.fit(mfccs.T) # .T는 전치를 의미, MFCC 행렬을 적절한 형태로 변환

# 결과 시각화
plt.figure(figsize=(10, 4))
librosa.display.specshow(mfccs, x_axis='time')
plt.colorbar()
plt.title('MFCC')
plt.tight_layout()
plt.show()

# 클러스터링 결과 예측
labels = gmm.predict(mfccs.T)
print("Labels:", labels)

GMMHMM

import numpy as np
import librosa  # 오디오 처리를 위한 라이브러리
from hmmlearn import hmm
from sklearn.model_selection import train_test_split

# 오디오 파일로부터 MFCC 특성을 추출하는 함수
def extract_mfcc_features(audio_files):
    features = []
    for file in audio_files:
        # 오디오 파일 읽기
        audio, sr = librosa.load(file)
        # MFCC 특성 추출
        mfccs = librosa.feature.mfcc(audio, sr=sr)
        features.append(mfccs.T)  # Transpose to match the hmmlearn input format
    return features

# 여기서는 audio_files 변수를 사용자가 제공해야 합니다. 예를 들어:
# audio_files = ['audio1.wav', 'audio2.wav', ..., 'audioN.wav']
# 해당 파일들은 모두 같은 클래스(예: 같은 단어나 발음)에 속해야 합니다.

# 오디오 파일 목록 (여기서는 예시로 사용자가 직접 제공해야 함)
audio_files = ['path/to/your/audio1.wav', 'path/to/your/audio2.wav']  # 예시 경로
mfcc_features = extract_mfcc_features(audio_files)

# 훈련 데이터 준비
# HMM은 길이가 다른 시퀀스를 처리할 수 있으므로 별도의 패딩이 필요 없습니다.
X = np.concatenate(mfcc_features)
lengths = [len(x) for x in mfcc_features]

# GMM-HMM 모델 생성 및 훈련
n_components = 4  # HMM 상태 수
n_mix = 2  # 각 상태에 대한 GMM 혼합 구성 요소의 수
model = hmm.GMMHMM(n_components=n_components, n_mix=n_mix, covariance_type='diag', n_iter=100)
model.fit(X, lengths)

# 모델 저장 또는 로딩
# 훈련된 모델 저장
import joblib
joblib.dump(model, 'gmmhmm_model.pkl')

# 저장된 모델 로딩
model = joblib.load('gmmhmm_model.pkl')

# 예측 (새로운 오디오 데이터로 테스트)
test_audio = ['path/to/your/test_audio.wav']
test_features = extract_mfcc_features(test_audio)
X_test = np.concatenate(test_features)
test_lengths = [len(x) for x in test_features]

# 모델을 사용하여 로그 확률 계산
logprob = model.score(X_test, test_lengths)
print(f"Log probability of the sequence: {logprob}")

GMM을 이해하기 위해 선행되어야할 지식들

GMM은 M개의 서로 다른 정규분포의 가중합으로 데이터를 표현하는 모델이라서, 다변량정규분포 파라미터 추정법 아는 게 필요

Univariate Normal Distribution (정규분포)

  • 정의:
    • 평균 μ, 분산 σ^2인 정규분포 N(μ,σ2)
    • N(x∣μ,σ2)=12πσexp⁡(−(x−μ)22σ2)N(x|\mu ,{\sigma}^2 )=\frac { 1 }{ \sqrt { 2\pi } \sigma } \exp\left( -\frac { { (x-\mu ) }^{ 2 } }{ 2{ \sigma }^{ 2 } } \right)
  • 비화
    = 가우스 분포. 하도 통계학자들이 가우스 분포 안따르면 비정상 자료라고 까지 해서 normal이라고 붙이게 됐다고 함. 오...
  • 예시
    주사위의 k번째 면이 n번 나올 확률을 이항분포의 예시로 설명할 수 있고, 여기서 엄청 동전을 많이 던졌을 때의 확률분포를 가우시안 분포로 말할 수 있음.

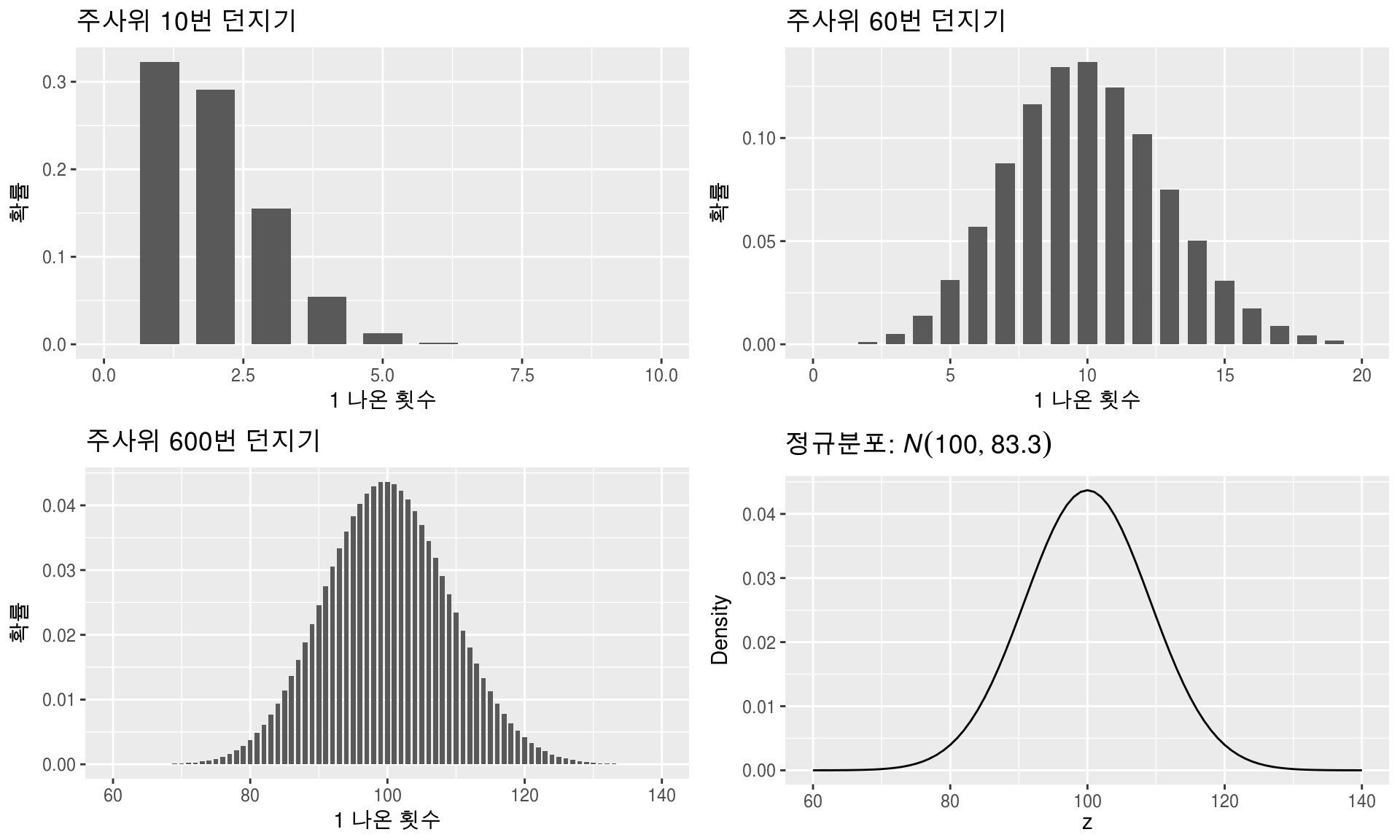
    https://bookdown.org/mathemedicine/Stat_book/normal-distribution.html

Multivariate Normal Distributution (다변량 정규분포)

  • 정의:

    • 정규분포를 다차원 공간으로 확장된 분포, 즉 정규분포의 input이 확률변수라면, 다변량 정규분포는 확률 벡터
    • N(x∣μ,Σ)=1(2π)D/2∣Σ∣1/2exp⁡{−12(x−μ)TΣ−1(x−μ)}N({\bf x}|{\pmb \mu}, {\bf \Sigma}) = \dfrac{1}{(2\pi)^{D/2}|{\bf \Sigma}|^{1/2}}\exp\left\{-\frac{1}{2}({\bf x}-{\pmb \mu})^T{\bf \Sigma}^{-1}({\bf x}-{\pmb \mu})\right\}
      • μ: D차원 평균 벡터
      • Σ: D×D 공분산(covariance) 행렬
        • 모든 변수에 대하여 분산과 공분산 값을 나타내는 정사각 행렬
        • 주 대각선 성분: 자기 자신의 분산 값
        • 이외: 공분산값
      • |Σ|: Σ의 행렬식(determinant)

  • 예시:
    서로 다른 공분산을 가진 3개의 2차원(X,Y) 다변량 정규분포 a,b,c (세로 X, 가로 Y)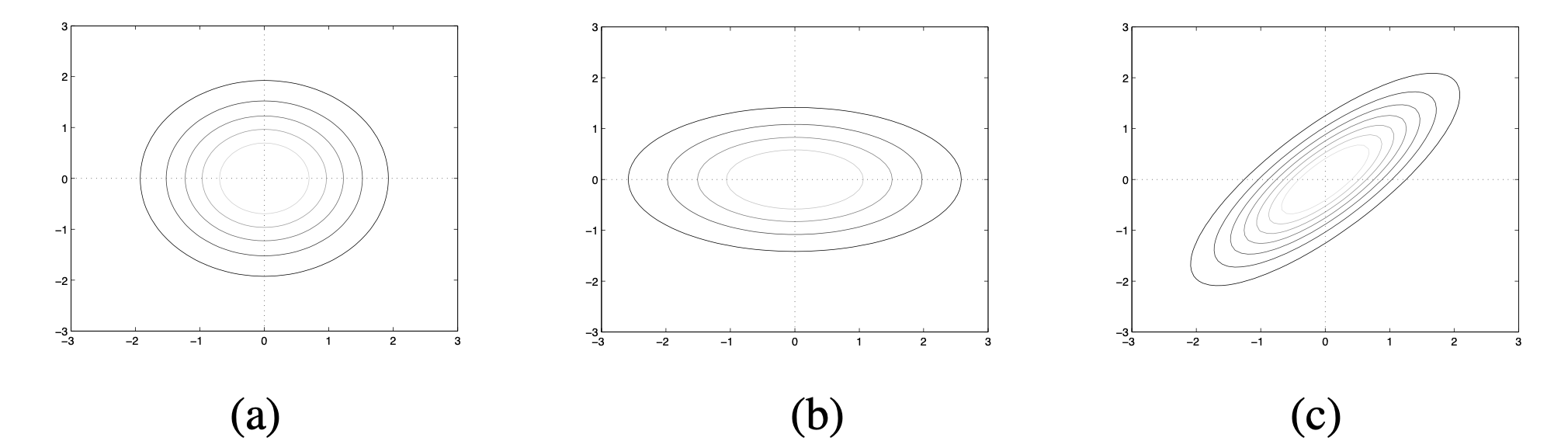

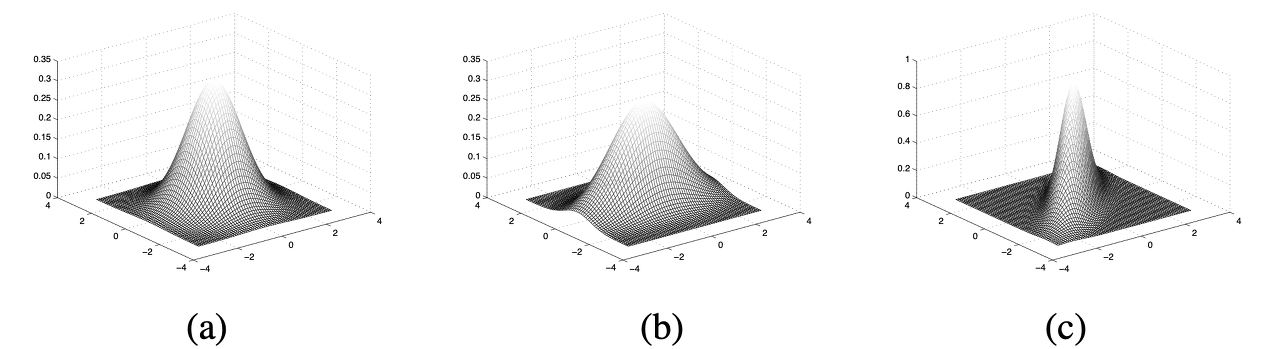
    • (a):Σa=(1001)\Sigma_a = \begin{pmatrix} 1 & 0\\ 0 & 1 \end{pmatrix}

      • 대각성분 이외의 요소값이 0인 대각행렬(diagonal matrix)
      • 대각성분의 모든 값이 1
      • X, Y 분산: 1
      • 공분산: 0
      • X와 Y의 분산이 서로 같고 둘의 공분산이 0이기 때문에 contour plot이 원형으로 나타남.

    • (b): Σb=(0.5002)\Sigma_b = \begin{pmatrix} 0.5 & 0\\ 0 & 2 \end{pmatrix}

      • X 분산: 0.6 / Y분산: 2
      • 공분산: 0
      • X와 Y의 분산이 서로 다르고 둘의 공분산이 0이기 때문에 plot이 타원
      • Y의 분산이 더 크기 때문에 가로축으로 길쭉

    • (c): Σc=(10.80.81)\Sigma_c = \begin{pmatrix} 1 & 0.8\\ 0.8 & 1 \end{pmatrix}

      • X와 Y 분산: 1
      • 공분산:0.8
      • plot이 가로축(Y), 세로축(X)에 정렬되지 않는 모습
      • 둘의 공분산이 0보다 크기 때문에 한 차원의 값을 알면 다른 차원의 값을 예측하는 데 도움이 됨.

Maximum Liklihood Estimator

  • 목적: 다변량 정규분포의 paremeter를 추정을 위해 MLE 사용.

  • Task (D차원 다변량 정규분포의 parameter 추정 시)
    (1) D차원 평균 벡터 μ
    (2) DxD 차원 공분산 행렬 Σ

  • Method

    • (1) log-likelihood function 구하고

    • (2) 이 함수를 최대화시키는 게 목적이므로 추정하고자 하는 parameter에 대해 각각 편미분을 해준다.

      • e.g.) μ 추정값 구하기
        • (1) μ에 대해 편미분 하고,
        • (2) 그 값을 0으로 두고 μ에 대해서 정리
          μ^MLE=∑i=1nXin\widehat{\boldsymbol{\mu}}^{MLE} = \frac{\sum_{i=1}^{n}\boldsymbol{X}_i}{n}
        • (3) Σ도 같은 방식으로
profile
누렁이
왈왈
이전 포스트

[ASR]PASE: Learning Problem-agnostic Speech Representations from Multiple Self-supervised Tasks & PASE+

다음 포스트

[ASR]Listen, Attend and Spell (2015)

2개의 댓글

comment-user-thumbnail
James Kim
2024년 2월 29일

잘봤습니다! 다만 내용이 어려워서 나중에 더 정독하겠습니다 ㅎㅎ

답글 달기
comment-user-thumbnail
fla1512
2024년 3월 11일

어려운 내용임에도 불구하고 깔끔하게 정리해주셔서 감사합니다!! 흐름을 이해하기 좋은 글이네요

답글 달기