[TIL Day13-2] Python으로 데이터 다루기 I - Numpy

Python으로 데이터 다루기 I - Numpy

Numpy를 더 공부해보고 싶다면 참고할 사이트
- 101 NumPy Exercises for Data Analysis (Python)
- NumPy v1.20 Manual

Numpy의 연산

• Vector와 Scalar 사이의 연산
  - 벡터의 각 원소에 대해서 연산을 진행
  

import numpy as np

x = np.array([1, 2, 3])
c = 5

print("더하기 : {}".format(x + c))
print("빼기 : {}".format(x - c))
print("곱하기 : {}".format(x * c))
print("나누기 : {}".format(x / c))

"""
# out
더하기 : [6 7 8]
빼기 : [-4 -3 -2]
곱하기 : [ 5 10 15]
나누기 : [0.2 0.4 0.6]
"""

• Vector와 Vector 사이의 연산
  - 벡터의 같은 인덱스끼리 연산이 진행!
  

y = np.array([1, 3, 5])
z = np.array([2, 9, 20])

print("더하기 : {}".format(y + z))
print("빼기 : {}".format(y - z))
print("곱하기 : {}".format(y * z))
print("나누기 : {}".format(y / z))

"""
# out
더하기 : [ 3 12 25]
빼기 : [ -1  -6 -15]
곱하기 : [  2  27 100]
나누기 : [0.5        0.33333333 0.25      ]
"""

• Array의 Indexing
  - numpy array에서 특정 위치의 원하는 원소를 가져오고 싶다면?
  - python list와 유사하게 진행
  

w = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

print(w[0, 0])

print(w[2, 3])

"""
#out
1
12
"""

• Array의 Slicing
  - numpy array에서 특정 범위의 원하는 원소들을 가지고 오는 방법?
  - python list와 유사하게 진행

w = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(w)

# 2, 3 -> 행: 인덱스 0~1 -> [0:2]
# 6, 7 -> 열: 인덱스 1~2 -> [1:3]

#[행 슬라이싱, 열 슬라이싱]
w[0:2, 1:3]

"""
#out
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
array([[2, 3],
       [6, 7]])
"""

# 모두 같은 행렬 반환
w[0:2, 0:4]

w[0:2]

w[0:2, :]

"""
#out
array([[1, 2, 3, 4],
       [5, 6, 7, 8]])
"""

• Array의 Broadcasting
  - numpy가 연산을 진행하는 특수한 방법!
  - 기본적으로 같은 type의 data에 대해서만 연산이 적용 가능하지만
  만약에 피연산자가 연산 가능하도록 변환이 가능하다면 연산이 가능하다. 이를 Broadcasting이라고 한다.
  

1. M x N, M x 1 -> M x N, M x N
   - M의 열을 N만큼 duplicate해서 element wise 연산 수행
   

a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
x = np.array([0, 1, 0])

print(a + x)

"""
#out
[[1 3 3]
 [4 6 6]
 [7 9 9]]
"""

x = x[:, None] # x를 전치

print(a + x)

"""
#out
[[1 2 3]
 [5 6 7]
 [7 8 9]]
"""

2. M x N, 1 x N, M x N, M x N
   - N의 행을 M만큼 duplicate해서 element wise 연산 수행
   

# = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
y = np.array([0, 1, -1])

print(a * y)

"""
#out
[[ 0  2 -3]
 [ 0  5 -6]
 [ 0  8 -9]]
"""

3. M x 1, 1 x N -> M x N, M x N
   - M의 열을 N만큼, N의 행을 M만큼 duplicate
   

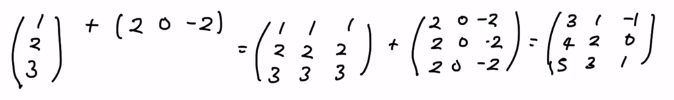
t = np.array([1, 2, 3])
t = t[:, None] # transpose
u = np.array([2, 0, -2])

print(t + u)

"""
#out
[[ 3  1 -1]
 [ 4  2  0]
 [ 5  3  1]]
"""

Numpy와 선형대수

• 영벡터(영행렬)
  - 원소가 모두 0인 벡터(행렬)
  - np.zeros(dim)을 통해 생성, dim은 값, 혹은 튜플 (, )

np.zeros((3, 3))

"""
#out
array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])
"""

• 일벡터(일행렬)
  - 원소가 모두 1인 벡터(행렬)
  - np.ones(dim)을 통해 생성, dim은 값, 혹은 튜플 (, )

np.ones((3, 3))

"""
#out
array([[1., 1., 1.],
       [1., 1., 1.],
       [1., 1., 1.]])
"""

• 대각행렬(diagonal matrix)
  - main diagonal을 제외한 성분이 0인 행렬
  - np.diag((main_diagonals))을 통해 생성

np.diag((1, 3, 5))

"""
#out
array([[1, 0, 0],
       [0, 3, 0],
       [0, 0, 5]])
"""

• 항등행렬(identity matrix)
  - main diagonal이 1인 대각행렬
  - np.eye(n, dtype)를 사용

np.eye(3, dtype=float)

"""
#out
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
"""

• 행렬곱(dot product)
  - 행렬간의 곱연산
  - np.dot() or @ 사용

mat_1 = np.array([[1, 4], [2, 3]])
mat_2 = np.array([[7, 9], [0, 6]])

mat_1.dot(mat_2)

mat_1 @ mat_2

"""
#out
array([[ 7, 33],
       [14, 36]])
"""

• 트레이스(trace)
  - main diagonal의 합
  - np.trace()를 사용

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

arr.trace()

"""
#out
15
"""

• 행렬식(determinant)
  - 행렬을 대표하는 값들 중 하나
  - 선형변환 과정에서 vector의 scaling 척도
  - np.linalg.det()으로 계산
  

arr_2 = np.array([[2, 3], [1, 6]])

np.linalg.det(arr_2)

"""
#out
9.000000000000002
"""

• 역행렬(inverse matrix)
  - 행렬 A에 대해 AB = BA = I를 만족하는 행렬 B = A^-1
  - np.linalg.inv()으로 계산
  

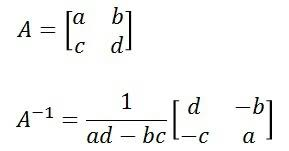
mat = np.array([[1, 4], [2, 3]])
mat_inv = np.linalg.inv(mat)

mat_inv

"""
#out
array([[-0.6,  0.8],
       [ 0.4, -0.2]])
"""

mat @ mat_inv

"""
#out
array([[1., 0.],
       [0., 1.]])
"""

• 고유값과 고유벡터(eigenvalue and eigenvector)
  - 정방행렬 A에 대해 𝐴𝑥=𝜆𝑥 를 만족하는 상수 𝜆 와 이에 대응하는 벡터 𝑥 를 각각 고유값과 고유벡터라 한다.
  - np.linalg.eig()으로 계산

mat = np.array([[2, 0, -2], [1, 1, -2], [0, 0, 1]])

np.linalg.eig(mat)

# 리턴값은 (고유값, 고유벡터) 순서이고
# 각 고유값에 대응되는 고유벡터를 column 기준으로 확인

"""
#out
(array([1., 2., 1.]),
 array([[0.        , 0.70710678, 0.89442719],
        [1.        , 0.70710678, 0.        ],
        [0.        , 0.        , 0.4472136 ]]))
"""

# validation
eig_val, eig_vec = np.linalg.eig(mat)

mat @ eig_vec[:, 0] # Ax
"""
#out
array([0., 1., 0.])
"""

eig_val[0] * eig_vec[:, 0] # (lambda)x

"""
#out
array([0., 1., 0.])
"""