1. 결정이론(Decision Theory)
- 결정이론이란?
새로운 값 x가 주어졌을 때 확률모델 p(x, t)에 기반해 최적의 결정을 내리는 것
- 추론단계: 결합확률분포 p(x, Ck)를 구하는 것 (p(Ck|x)를 직접 구하는 경우도 있음)
- 결정단계: 상황에 대한 확률이 주어졌을 때 어떻게 최적의 결정을 내릴 것인지?
이진분류(Binary Classification)의 경우
-
결정영역(decision region): 클래스 i에 속하는(속한다고 판단되는) 모든 x의 집합
Ri = {x : pred(x) = Ci} -
분류오류 확률(probability of misclassification)
p(mis) = p(x ∈ R1, C2) + P(x ∈ R2, C1)
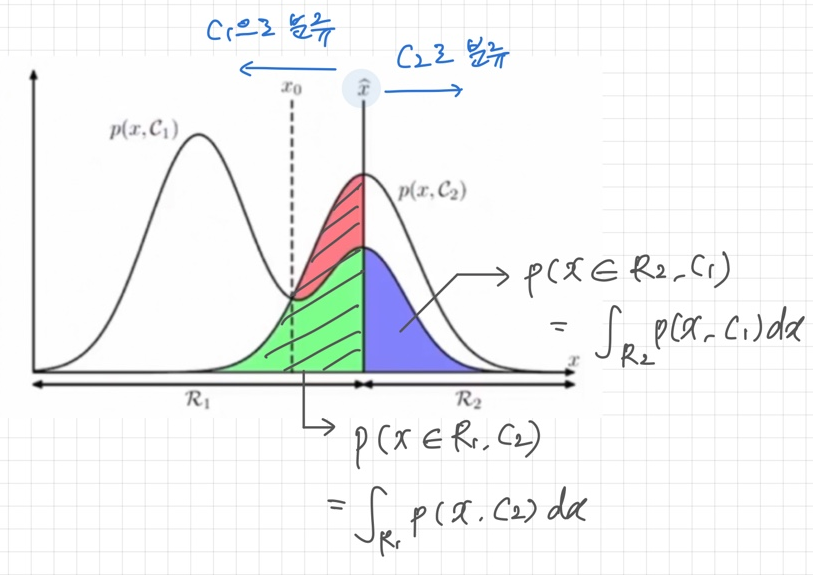
아래 그림에서 색칠된 세 영역의 넓이의 합이 분류오류확률이다. 녹색 + 파란색 영역의 합은 불변이지만, 빨간색 영역을 최소화하는 x를 찾으면 오류를 최소화할 수 있다.
-
오류를 최소화하려면 다음조건을 만족하는 x를 R1에 할당해야 한다.
p(x, C1) > p(x, C2)
⇔ p(C1|x)p(x) > p(C2|x)p(x)
⇔ p(C1|x) > p(C2|x)
다중분류(Multiclass Classification)의 경우
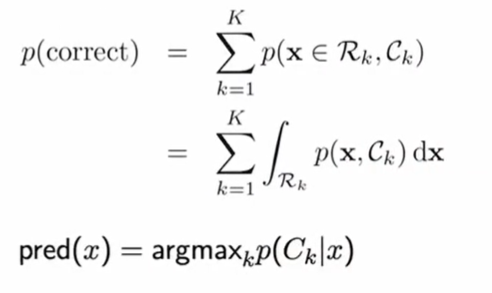
결정이론의 목표(분류의 경우)
결합확률분포 p(x, Ck)가 주어졌을 때 최적의 결정영역들 R1, ... , Rk를 찾는 것
⇒ 즉, x가 주어졌을 때 예측값(1, ... , K 중의 값)을 돌려주는 함수 ^C(x) 중 '최적의 함수'를 찾는 것
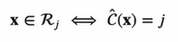
기대손실 최소화(Minimizing the Expected Loss)
모든 결정이 동일한 리스크를 갖는 것은 아니다! 손실행렬 L이 주어졌을 때 기대손실을 최소화하자.
- 손실행렬(loss matrix): k * k 크기의 행렬
- Lkj: Ck에 속하는 x를 Cj로 분류할 때 발생하는 손실(또는 비용)
- 행은 실제 정답 클래스, 열은 분류된 클래스
- 기대손실
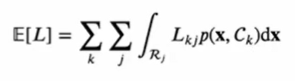
- 데이터에 대한 모든 지식이 확률분포로 표현되고 있다. 한 데이터샘플 x의 실제 클래스를 결정론적으로 알고 있는 것이 아니라 그것의 확률만을 알 수 있다고 가정한다. 즉, 우리가 관찰할 수 있는 샘플은 확률분포 p(x, Ck)를 통해서 생성된 것이라고 간주한다.
- ^C(x)를 x가 주어졌을 때 예측값을 돌려주는 함수라고 하면, 위의 E[L]식을 아래와 같이 표현할 수 있다.
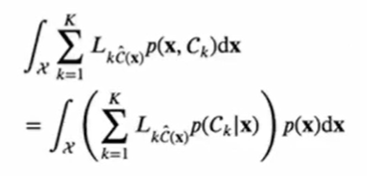
- 이렇게 표현된 E[L]은 ^C(x)의 범함수이고, 이 범함수를 최소화시키는 함수 ^C(x)를 찾으면 된다.
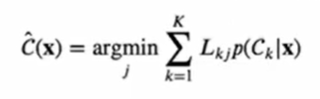
- 예제: 의료진단

회귀문제의 경우
여기서부터 상당히 이해가 어려웠다. 추후에 여기를 참고하여 조금 더 정리할 것.
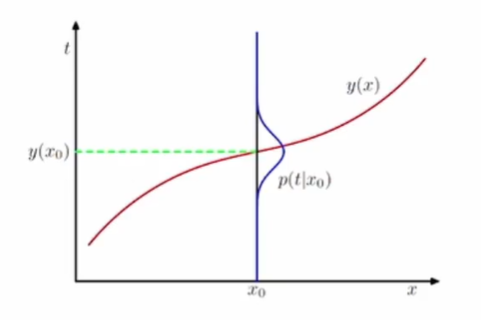
목표값 t ∈ R
손실함수: L(t, y(x)) = {y(x) - t}^2
손실함수의 기댓값을 최소화하는 함수 y를 구하는 것이 목표!

- x를 위한 최적의 예측값(즉, 손실함수의 기댓값을 최소화시키는 예측값)은
y(x) = Et[t|x](x가 주어졌을 때 t의 기댓값)이다.
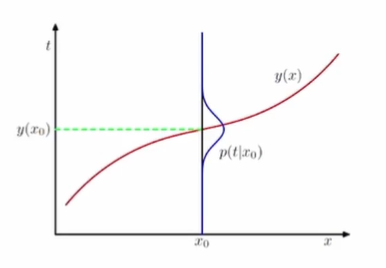
결정문제를 위한 몇 가지 방법들
a. 분류문제의 경우
-
확률모델에 의존하는 경우
- 생성모델(generative model): 먼저 각 클래스 Ck에 대해 분포 p(X|Ck)와 사전확률 p(Ck)를 구한 다음 베이즈정리를 사용해서 사후확률 p(Ck|x)를 구한다. 결합분포에서 데이터를 샘플링해서 '생성'할 수 있으므로 생성모델이라고 부른다.
- 식별모델(discriminative model): 모든 분포를 다 계산하지 않고 오직 사후확률 p(Ck|x)을 구한다. -
판별함수에 의존하는 경우
- 판별함수(discriminant function): 입력 x를 클래스로 할당하는 판별함수를 찾는다. 확률값은 계산하지 않는다.
b. 회귀문제의 경우
-
결합분포 p(x, t)를 구하는 추론문제를 먼저 푼 다음, 조건부확률분포 p(t|x)를 구한다. 그리고 주변화(marginalize)를 통해 Et[t|x]를 구한다.
-
조건부확률분포 p(t|x)를 구하는 추론문제를 푼 다음 주변화를 통해 Et[t|x]를 구한다.
-
y(x)를 직접적으로 구한다.