참고서적
- Pattern Recognition and Machine Learning by Christopher Bishop PDF 다운로드
- Deep Learning by Ian Goodfellow, Yoshua Bengio and Aaron Courville PDF 다운로드
- Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow(2nd Edition) 코드 및 동영상 강의
1. Machine Learning 소개
- Machine Learning이란?
- 경험을 통해 자동으로 개선하는 컴퓨터 알고리즘의 연구
- 학습 데이터: 입력벡터들 x1, ... , xn, 목표값들 t1, ... , tn
- 머신러닝 알고리즘의 결과는 목표값을 잘 예측하는 함수 y(x)
핵심개념들
- 학습단계(training or learning phase): 함수 y(x)를 학습데이터에 기반해 결정하는 단계
- 시험셋(test set): 모델을 평가하기 위해 사용하는 새로운 데이터
- 일반화(generalization): 모델에서 학습에 사용된 데이터가 아닌 이전에 접하지 못한 새로운 데이터에 대해 올바른 예측을 수행하는 역량
- 지도학습(supervised learning): target이 주어진 경우
- 분류(classification)
- 회귀(regression) - 비지도학습(unsupervised learning): target이 없는 경우
- 군집(clustering)
다항식 곡선 근사(Polynomal Curve Fitting)
- 학습데이터: 입력벡터 X = (x1, ... , xn)^T, t = (t1, ... , tn)^T
- 목표: 새로운 입력벡터 x^이 주어졌을 때 목표값 t^을 예측하는 것
- 확률이론(probability theory): 예측값의 불확실성을 정량화시켜 표현할 수 있는 수학적인 프레임워크 제공
- 결정이론(decision theory): 확률적 표현을 바탕으로 최적의 예측을 수행할 수 있는 방법론 제공
- A polynomail function linear in w
- w: 찾아내야 하는 값, m + 1개의 모델 parameter
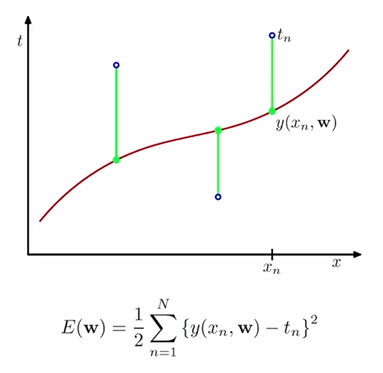
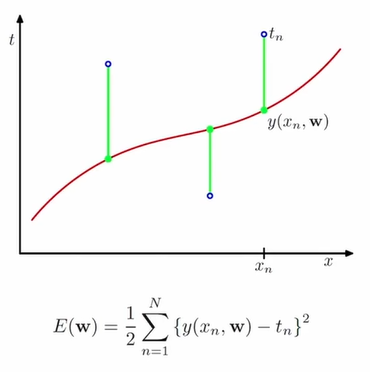
오차함수(Error Function)
실제값 tn과 예측값 y(xn, w)의 오차제곱합을 오차함수 E(w)로 이용한다. 오차함수의 최솟값은 실제값과 예측값이 같을 때, 즉 오차가 0일 때이다.
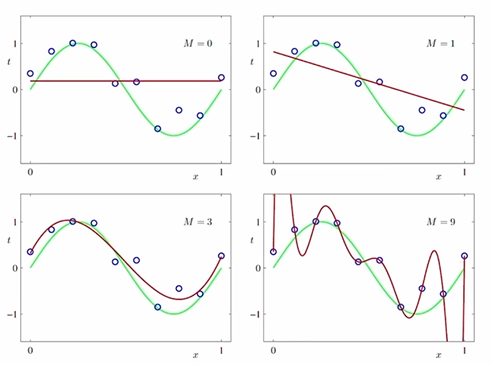
과소적합(Under-fitting)과 과대적합(Over-fitting)
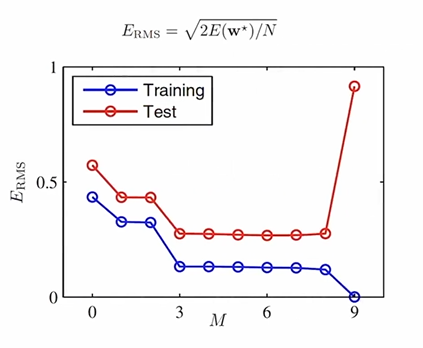
- 과소적합 및 과대적합의 판단: 학습셋과 시험셋의 오차 비교
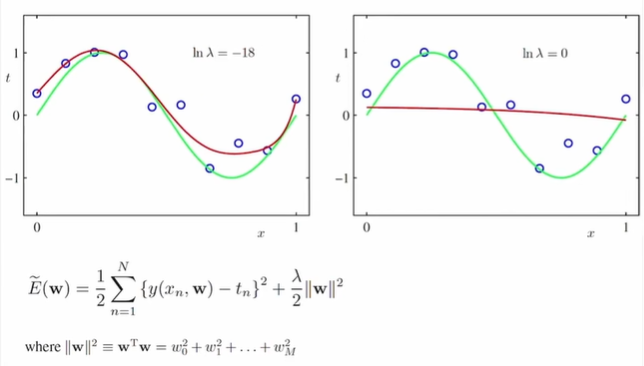
규제화(Regularization)
- 파라미터 절댓값이 너무 커지지 않도록 오차함수를 수정하는 방식으로 간단하게 적용 가능
- λ값이 작을수록 기존의 오차함수(오차제곱합)과 같아지므로 규제가 완화된다.
- λ값이 너무 커지면 오히려 과소적합될 수 있으니 주의
2. 확률이론(Probability Theory)
확률변수(Random Variable)
확률변수 X는 표본의 집합 S의 원소 e를 실수값 X(e) = x에 대응시키는 함수이다. 예를 들어, 동전 한 개를 던져 앞면 혹은 뒷면이 나오는 사건의 집합 S = {H, T}이 있을 때 X(H) = 0, X(T) = 1로 대응시킬 수 있다.
- 대문자 X, Y, ...: 확률변수
- 소문자 x, y, ...: 확률변수가 가질 수 있는 값
- 확률 P는 집합 S의 부분집합을 실수값에 대응시키는 함수
- P[X = x]
- P[X <= x]
- X = x, X <= x는 집합 S의 부분집합을 정의한다.
연속확률변수 (Continuous Random Variables)
- 누적분포함수(cumulative distribution function, CDF): F(x) = P[X ∈ (-∞, x)]
- 누적분포함수 F(x)를 가진 확률변수 X에 대해서 다음을 만족하는 함수 f(x)가 존재한다면 X를 연속확률변수라고 부르고, f(x)를 X의 확률밀도함수(probability density function, PDF)라고 부른다.

확률변수의 성질
전에 올린 게시글에 잘 정리해 두었다.
확률변수의 함수(Functions of Random Variables)
확률변수 X의 함수 Y = f(X)도 확률변수이다. 확률변수 X의 함수 Y = g(X)와 역함수 w(Y) = X가 주어졌을 때(일대일 대응) 다음이 성립한다. 즉, 새로운 확률변수 Y의 밀도함수는 X의 밀도함수에 특정한 값을 곱하여 구할 수 있다.
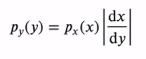
- k차원의 확률변수 벡터 x = (x1, ... , xk)가 주어졌을 때
k개의 x에 관한 함수들 yi = gi(x) for i = 1, ... , k는 새로운 확률변수벡터 y = (y1, ... , yk)를 정의한다. 이를 간략하게 y = g(x)로 나타내자.
만약 y = g(x)가 일대일 변환인 경우(x = w(y)로 유일한 해를 가질 때), y의 결합확률밀도함수는 다음과 같다.

- 예제를 풀어보자.


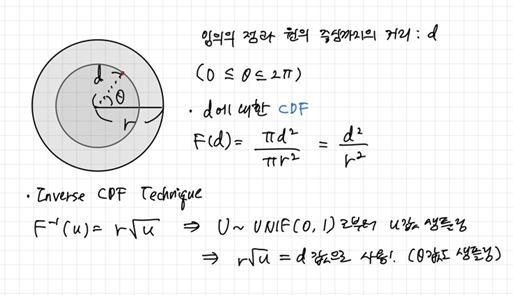
Inverse CDF Technique
확률변수 X의 분포를 따르는 sample들을 만들 때 사용할 수 있는 기법이다. 더욱 자세한 설명은 여기를 참고하여 이해하였다.

- 예제: 반경이 r인 원 안에 랜덤하게 점들을 찍는 프로그램을 만드려면 어떻게 해야 할까?
빈도주의 vs 베이지안(Frequentist vs Bayesian)
확률을 해석하는 두 가지 다른 관점
- 빈도주의: 반복가능한 사건들의 빈도수에 기반
- 베이지안: 불확실성을 정량적으로 표현
반복가능하지 않은 사건일 경우(ex. 북극 얼음이 이번 세기말까지 녹아 없어질 확률?), 우리가 이미 알고 있는 정보(얼음이 녹고 있는 속도)에 근거해 확률을 정량적으로 나타낼 수 있고 새로 수집하는 정보에 따라 확률을 업데이트할 수 있다.
앞서 언급한 다항식 곡선 근사문제에서의 계수 w(즉, 모델의 파라미트)에 대한 우리의 지식을 확률적으로 나타내려고 한다.
-
베이지안 방식:
- w에 대한 사전지식 p(w) ⇒ 사전확률(prior)
- 새로운 데이터 D = {t1, ... , tn}를 관찰하고 난 뒤의 조건부확률 p(D|w) ⇒ 우도함수(likelihood function)
(특정 w값에 대해 D의 관찰값이 얼마나 '가능성'이 있는지를 나타낸다. w에 관한 함수임을 기억하자.)
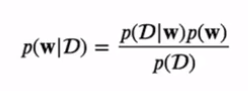
- p(w|D)는 D를 관찰하고 난 뒤의 w에 대한 불확실성을 표현
- 사후확률(posterior) ∝ 우도(likelihood) X 사전확률(prior)
- 장점: 사전확률을 모델에 포함시킬 수 있고, 극단적인 확률을 피할 수 있다. -
빈도주의 방식:
- w가 고정된 파라미터이고 최대우도와 같은 추정자(estimator)를 사용해서 그 값을 구한다.
- 구해진 파라미터의 불확실성은 부트스트랩(bootstrap) 방법을 써서 구할 수 있다.
곡선근사(Curve Fitting): 확률적 관점
학습데이터 라고 할 때, 목표값 의 불확실성을 다음과 같이 확률분포로 나타낼 수 있다. 추후 업데이트 예정...
