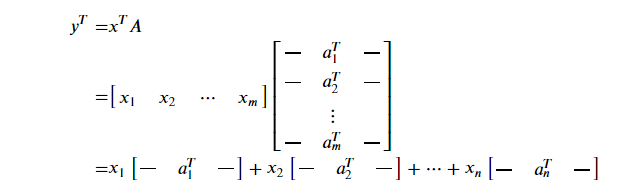[TIL Day26] Machine Learning 기초 - Linear Algebra

선형대수와 행렬미분의 기초를 배우고 간단한 머신러닝 알고리즘(PCA)을 유도해보고자 한다.

1. 기본 표기법 (Basic Notation)

• $A\in \mathbb{R}^{m\times n}$는 $m$개의 행과 $n$개의 열을 가진 행렬을 의미한다.
• $x \in \mathbb{R}^n$는 $n$개의 원소를 가진 벡터를 의미한다.
  - $n$차원 벡터는 $n$개의 행과 1개의 열을 가진 행렬로 생각할 수 있다. 이것을 열벡터(column vector)로 부르기도 한다.
  - 만약, 명시적으로 행벡터(row vector)를 표현하고자 한다면, $x^T$($T$는 transpose를 의미)로 쓴다.
• 벡터 $x$의 $i$번째 원소는 $x_i$로 표시한다.
• $a_{ij}$(또는 $A_{ij}, A_{i,j}$)는 행렬 $A$의 $i$번째 행, $j$번째 열에 있는 원소를 표시한다.
• $A$의 $j$번째 열을 $a_j$ 혹은 $A_{:,j}$로 표시한다.
  $A = \begin{bmatrix} \vert & \vert & & \vert\\ a_1 & a_2 & \cdots & a_n\\ \vert & \vert & & \vert \end{bmatrix}$
• $A$의 $i$번째 행을 $a_i^T$ 혹은 $A_{i,:}$로 표시한다.
  $A = \begin{bmatrix} \rule[.5ex]{1.7ex}{0.5pt} & a_1^T & \rule[.5ex]{1.7ex}{0.5pt}\\ \rule[.5ex]{1.7ex}{0.5pt} & a_2^T & \rule[.5ex]{1.7ex}{0.5pt}\\ & \vdots &\\ \rule[.5ex]{1.7ex}{0.5pt} & a_m^T & \rule[.5ex]{1.7ex}{0.5pt} \end{bmatrix}$
• Python에서의 벡터, 행렬 표현방법

import numpy as np
A = np.array([
    [10,20,30],
    [40,50,60]
])

A.shape 
## output
# (2, 3)

# column vector
j = 1
A[:, j] 
## output
# array([20, 50])

# row vector
i = 1
A[i, :]
## output
# array([40, 50, 60])

---

2. 행렬의 곱셈 (Matrix Multiplication)

두 개의 행렬 $A\in \mathbb{R}^{m\times n}$, $B\in \mathbb{R}^{n\times p}$의 곱 $C = AB \in \mathbb{R}^{m\times p}$는 다음과 같이 정의된다.

$C_{ij} = \sum_{k=1}^n A_{ik}B_{kj}$

벡터 × 벡터 (Vector-Vector Products)

• 내적(inner product)
  두 개의 벡터 $x, y\in \mathbb{R}^n$이 주어졌을 때 내적(inner product 또는 dot product) $x^Ty$는 다음과 같이 정의된다.

x = np.array([1, 2, 3])
y = np.array([4, 5, 6])
x.dot(y) # 32
y.dot(x) # 32

# 결과값이 scalar인 것을 확인

• 외적(outer product)
  두 개의 벡터 $x\in \mathbb{R}^m, y\in \mathbb{R}^n$이 주어졌을 때 외적(outer product) $xy^T\in \mathbb{R}^{m\times n}$는 다음과 같이 정의된다.

x = np.expand_dims(x, axis=1) # 열벡터로
y = np.expand_dims(y, axis=0) # 행벡터로
x.shape, y.shape # ((3, 1), (1, 3))

np.matmul(x,y)
## output
# array([[ 4,  5,  6],
#       [ 8, 10, 12],
#       [12, 15, 18]])

# 결과가 3*3의 행렬임을 확인

• 외적을 이용하여 모든 열들이 동일한 벡터를 가진 행렬 표현하기
  아래 행렬 $A$는 모든 열들이 동일한 벡터 $x$를 가지고 있다. 외적을 이용하면 간편하게 $x\mathbf{1}^T$로 나타낼 수 있다($\mathbf{1}\in \mathbb{R}^n$는 모든 원소가 1인 $n$차원 벡터).
  $A = \begin{bmatrix} \vert & \vert & & \vert\\ x & x & \cdots & x\\ \vert & \vert & & \vert \end{bmatrix} = \begin{bmatrix} x_1 & x_1 & \cdots & x_1\\ x_2 & x_2 & \cdots & x_2\\ \vdots & \vdots & \ddots & \vdots\\ x_m & x_m & \cdots & x_m \end{bmatrix} = \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_m \end{bmatrix} \begin{bmatrix} 1 & 1 & \cdots & 1 \end{bmatrix} = x\mathbf{1}^T$

# column vector
x = np.expand_dims(np.array([1, 2, 3]), axis=1)

ones = np.ones([1,4])

A = np.matmul(x, ones)
A
## output
# array([[1., 1., 1., 1.],
#       [2., 2., 2., 2.],
#       [3., 3., 3., 3.]])

행렬 × 벡터 (Matrix-Vector Products)

행렬 $A\in \mathbb{R}^{m\times n}$와 (열)벡터 $x\in \mathbb{R}^n$의 곱인 벡터 $y = Ax \in \mathbb{R}^m$를 몇 가지 측면에서 바라볼 수 있다.

• 열벡터를 오른쪽에 곱하고($Ax$), $A$가 행의 형태로 표현되었을 때
  $a_m^T$와 벡터 $x$의 dot product
  $y = Ax = \begin{bmatrix} \rule[.5ex]{1.7ex}{0.5pt} & a_1^T & \rule[.5ex]{1.7ex}{0.5pt}\\ \rule[.5ex]{1.7ex}{0.5pt} & a_2^T & \rule[.5ex]{1.7ex}{0.5pt}\\ & \vdots &\\ \rule[.5ex]{1.7ex}{0.5pt} & a_m^T & \rule[.5ex]{1.7ex}{0.5pt} \end{bmatrix} x = \begin{bmatrix} a_1^Tx\\ a_2^Tx\\ \vdots\\ a_m^Tx \end{bmatrix}$

A = np.array([
    [1,2,3],
    [4,5,6]
])

ones = np.ones([3,1])

np.matmul(A, ones)
## output
# array([[ 6.],
#       [15.]])

• 열벡터를 오른쪽에 곱하고($Ax$), $A$가 열의 형태로 표현되었을 때
  합의 형태로 벡터가 표현됨
  $y = Ax = \begin{bmatrix} \vert & \vert & & \vert\\ a_1 & a_2 & \cdots & a_n\\ \vert & \vert & & \vert \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} \vert\\ a_1\\ \vert \end{bmatrix} x_1 + \begin{bmatrix} \vert\\ a_2\\ \vert \end{bmatrix} x_2 + \cdots + \begin{bmatrix} \vert\\ a_n\\ \vert \end{bmatrix} x_n$

A = np.array([
    [1,0,1],
    [0,1,1]
])
x = np.array([
    [1],
    [2],
    [3]
])
np.matmul(A, x)
## output
# array([[4],
#       [5]])

for i in range(A.shape[1]):
    print('a_'+str(i)+':', A[:,i], '\tx_'+str(i)+':', x[i], '\ta_'+str(i)+'*x_'+str(i)+':', A[:,i]*x[i])
## output
# a_0: [1 0] 	x_0: [1] 	a_0*x_0: [1 0]
# a_1: [0 1] 	x_1: [2] 	a_1*x_1: [0 2]
# a_2: [1 1] 	x_2: [3] 	a_2*x_2: [3 3]

• 행벡터를 왼쪽에 곱하고($x^TA$), $A$가 열의 형태로 표현되었을 때
  $A\in \mathbb{R}^{m\times n}$, $x\in \mathbb{R}^m$, $y\in \mathbb{R}^n$일 때, $y^T = x^TA$

• 행벡터를 왼쪽에 곱하고($x^TA$), $A$가 행의 형태로 표현되었을 때
  

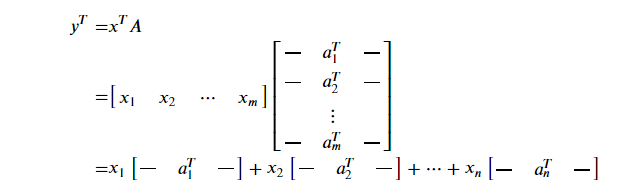
행렬 × 행렬 (Matrix-Matrix Products)

• 일련의 벡터 × 벡터 연산으로 표현하는 경우
  - $A$가 행으로, $B$가 열로 표현되었을 때
  $A\in \mathbb{R}^{m\times n}$, $B\in \mathbb{R}^{n\times p}$, $a_i \in \mathbb{R}^n$, $b_j \in \mathbb{R}^n$이기 때문에 내적값들이 자연스럽게 정의된다.

  $C = AB = \begin{bmatrix} \rule[.5ex]{1.7ex}{0.5pt} & a_1^T & \rule[.5ex]{1.7ex}{0.5pt}\\ \rule[.5ex]{1.7ex}{0.5pt} & a_2^T & \rule[.5ex]{1.7ex}{0.5pt}\\ & \vdots &\\ \rule[.5ex]{1.7ex}{0.5pt} & a_m^T & \rule[.5ex]{1.7ex}{0.5pt} \end{bmatrix} \begin{bmatrix} \vert & \vert & & \vert\\ b_1 & b_2 & \cdots & b_p\\ \vert & \vert & & \vert \end{bmatrix} = \begin{bmatrix} a_1^Tb_1 & a_1^Tb_2 & \cdots & a_1^Tb_p\\ a_2^Tb_1 & a_2^Tb_2 & \cdots & a_2^Tb_p\\ \vdots & \vdots & \ddots & \vdots\\ a_m^Tb_1 & a_m^Tb_2 & \cdots & a_m^Tb_p\\ \end{bmatrix}$

  - $A$가 열로 $B$가 행으로 표현되었을 때
  $AB$는 모든 $i$에 대해서 $a_i\in \mathbb{R}^m$와 $b_i\in \mathbb{R}^p$의 외적의 합이다.
  $a_i b_i^T$의 차원은 $m\times p$이다 ($C$의 차원과 동일).

  $C = AB = \begin{bmatrix} \vert & \vert & & \vert\\ a_1 & a_2 & \cdots & a_n\\ \vert & \vert & & \vert \end{bmatrix} \begin{bmatrix} \rule[.5ex]{1.7ex}{0.5pt} & b_1^T & \rule[.5ex]{1.7ex}{0.5pt}\\ \rule[.5ex]{1.7ex}{0.5pt} & b_2^T & \rule[.5ex]{1.7ex}{0.5pt}\\ & \vdots &\\ \rule[.5ex]{1.7ex}{0.5pt} & b_n^T & \rule[.5ex]{1.7ex}{0.5pt} \end{bmatrix} = \sum_{i=1}^n a_i b_i^T$

• 일련의 행렬 × 벡터 연산으로 표현하는 경우
  - $B$가 열로 표현되었을 때

  $C = AB = A \begin{bmatrix} \vert & \vert & & \vert\\ b_1 & b_2 & \cdots & b_p\\ \vert & \vert & & \vert \end{bmatrix} = \begin{bmatrix} \vert & \vert & & \vert\\ Ab_1 & Ab_2 & \cdots & Ab_p\\ \vert & \vert & & \vert \end{bmatrix}$

  - $A$가 행으로 표현되었을 때

  $C = AB = \begin{bmatrix} \rule[.5ex]{1.7ex}{0.5pt} & a_1^T & \rule[.5ex]{1.7ex}{0.5pt}\\ \rule[.5ex]{1.7ex}{0.5pt} & a_2^T & \rule[.5ex]{1.7ex}{0.5pt}\\ & \vdots &\\ \rule[.5ex]{1.7ex}{0.5pt} & a_m^T & \rule[.5ex]{1.7ex}{0.5pt} \end{bmatrix} B = \begin{bmatrix} \rule[.5ex]{1.7ex}{0.5pt} & a_1^TB & \rule[.5ex]{1.7ex}{0.5pt}\\ \rule[.5ex]{1.7ex}{0.5pt} & a_2^TB & \rule[.5ex]{1.7ex}{0.5pt}\\ & \vdots &\\ \rule[.5ex]{1.7ex}{0.5pt} & a_m^TB & \rule[.5ex]{1.7ex}{0.5pt} \end{bmatrix}$

---

3. 중요 연산과 성질들 (Operations and Properties)

• 정방행렬(square matrix): 행과 열의 개수가 동일

• 상삼각행렬(upper triangular matrix): 정방행렬이며 주대각선 아래 원소들이 모두 0

• 하삼각행렬(lower triangular matrix): 정방행렬이며 주대각선 위 원소들이 모두 0

• 대각행렬(diagonal matrix): 정방행렬이며 주대각선 제외 모든 원소가 0

# numpy의 diag함수를 사용해서 대각행렬을 생성할 수 있음
np.diag([4, 5, 6])
## output
# array([[4, 0, 0],
#       [0, 5, 0],
#       [0, 0, 6]])


# diag 함수에 행렬을 전달하면 주대각선 값들을 얻을 수 있음
D = np.array([
        [1, 2, 3],
        [4, 5, 6],
        [7, 8, 9],
    ])
np.diag(D)
## output
# array([1, 5, 9])

• 단위행렬(identity matrix): 대각행렬이며 주대각선 원소들이 모두 1인 행렬, $I$로 표시

# numpy의 eye 함수를 사용하면 원하는 크기의 단위행렬을 생성할 수 있음
np.eye(3)
## output
# array([[1., 0., 0.],
#       [0., 1., 0.],
#       [0., 0., 1.]])

내용이 길어지는 관계로 다음 게시글에 이어서 작성하겠다.