[TIL Day27] ML 기초 실습 과제

0. 과제 요구사항

문제설명

데이터셋을 사용하여 음식배달 서비스를 위한 예측모델을 만들어봅시다.
이 모델이 예측하는 값은 “음식배달에 걸리는 시간"입니다. 배달시간을 정확하게 예측하는 것은 사용자의 경험에 많은 영향을 미치게 됩니다.
예측된 배달시간보다 실제 배달시간이 더 걸린 경우(under-prediction)가 반대의 경우(over-prediction)보다 두 배로 사용자의 경험에 안 좋은 영향을 준다고 알려져 있습니다.
가능한 실제 배달시간과 가까운 값을 예측하되 동시에 under-prediction을 최소화하는 것이 좋은 예측모델입니다.

학습/테스트 데이터

• Restaurant, Location, Cuisines, AverageCost, MinimumOrder, Rating, Votes, Reviews 속성들을 모델의 입력속성으로 사용하세요. 모델의 학습목표는 DeliveryTime입니다.
• 이 데이터에서 랜덤하게 20%를 추출해서 테스트 데이터로 사용하고 나머지는 학습데이터로 사용하세요.

성능측정지표

• MAE(Mean Absolute Error)
• Under-prediction의 비율(under-prediction 개수 / 테스트 데이터 샘플 수)

1. 탐색적 데이터 분석

• 변수 파악하기
  - Restaurant: 음식점 고유의 ID
  - Location: 음식점의 위치
  - Cuisines: 음식점에서 취급하는 메뉴
  - Average_Cost: (고객당) 평균 주문가격
  - Minimum_Order: 최소 주문량(또는 금액)
  - Rating: 음식점의 평점
  - Votes: 평점을 남긴 고객 수
  - Reviews: 리뷰 수
  - Delivery_Time: 배달시간(예측하고자 하는 값)

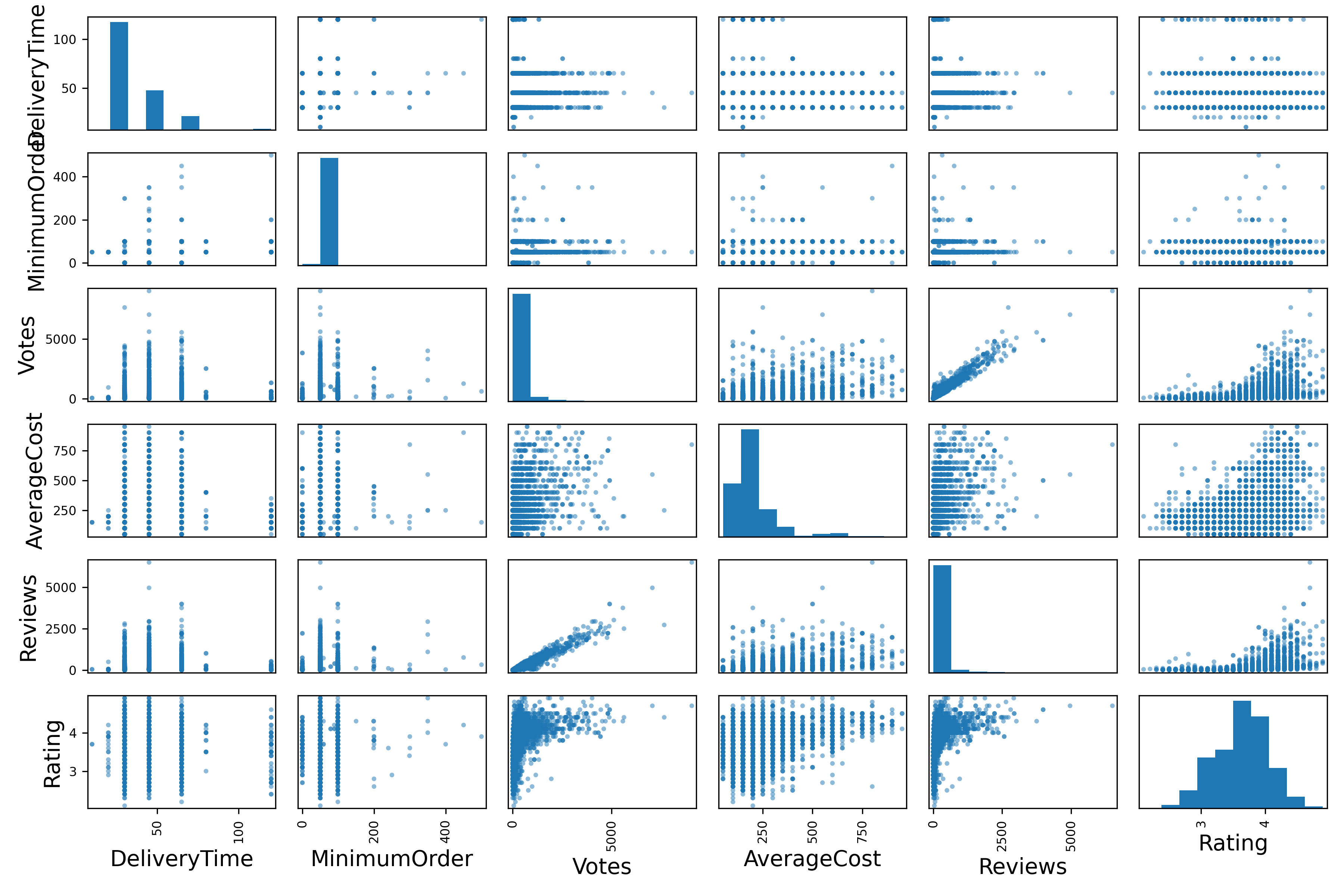
• 변수 간 상관관계 확인

  

2. 머신러닝을 위한 데이터 준비

결측치 확인 및 처리

- sklearn의 SimpleImputer를 사용하여 중앙값으로 수치형 변수의 결측치를 채워주었다.

 from sklearn.impute import SimpleImputer
 imputer = SimpleImputer(strategy="median")

새로운 변수 정의

• ReviewRatio: 평점을 남긴 사람들 중 리뷰를 쓴 사람의 비율

  dataset_tr['ReviewRatio'] = dataset_tr['Reviews'] / dataset_tr['Votes']

• CuisinesNum: 음식점의 메뉴 개수

  dataset_tr['CuisinesNum'] = dataset_tr['Cuisines'].apply(lambda x: len(x.split(', ')))

• Area: Location을 더 큰 범주(주소의 가장 뒤에 나오는 도시 이름)로 분류

   dataset_tr['Area'] = dataset_tr['Location'].apply(lambda x: x.split(',')[-1].strip())

3. 모델 학습

회귀 모델로는 ExtraTreesRegressor를 사용하였다.

변수 조합 실험

• 수치형 변수들[AverageCost, MinimumOrder, Rating, Votes, Reviews, CuisinesNum, ReviewRatio]과 범주형 변수들[Area(One-hot encoded), Cuisines(get dummies seperated by comma)]의 여러 조합을 비교해보았다.

  평가지표	모든 변수(129개 columns) 학습	수치형 변수들 + Area(One-hot encoded) 변수만 학습	수치형 변수들만 학습
  Mean MAE(10-fold CV)	5.26	5.69	4.97

• 결과적으로 수치형 변수들만 학습한 모델의 MAE가 가장 작아서, 이 변수들만 가지고 모델을 학습시키기로 했다.

모델 세부 튜닝

• GridSearchCV를 이용하여 하이퍼파라미터 튜닝을 진행한 결과, ExtraTreesRegressor(max_depth=30, n_estimators=150, random_state=42)의 성능이 가장 좋았다.

    from sklearn.model_selection import GridSearchCV

    param_grid = {'n_estimators': [50, 100, 150], 
    'min_samples_leaf': [1, 2, 3],
    'min_samples_split': [2, 5, 10],
    'max_depth': [30, 50, 100, None]}

    et_reg = ExtraTreesRegressor(random_state=42)

    grid_search = GridSearchCV(et_reg, param_grid, cv=5,
    scoring='neg_mean_absolute_error',
    return_train_score=True)
    grid_search.fit(X_train[num_attribs], Y_train)

    grid_search.best_estimator_
    # ExtraTreesRegressor(max_depth=30, n_estimators=150, random_state=42)

4. 모델 평가

테스트셋으로 최종 모델의 성능 평가

• MAE: 9.12

    pred = et_tuned.predict(X_test[num_attribs])

    from sklearn.metrics import mean_absolute_error
    mean_absolute_error(Y_test, pred)
    # 9.115545884014619

• Under-prediction 비율: 0.23

      def get_under_pred_ratio(pred, labels):
      cnt = 0
      for i, j in zip(pred, labels):
          if i < j:
              cnt += 1
      return cnt / len(labels)
                   
      get_under_pred_ratio(pred, Y_test)
      # 0.23253717890941866