확률분포 Part 1: 이산확률분포에 대해 알아본다.
아래 내용은 여기를 참고하여 더 공부하자.
밀도추정(Density Estimation)
N개의 관찰데이터(observations) x1,…xN가 주어졌을 때 분포함수 p(x)를 찾는 것
-
p(x)를 파라미터화된 분포로 가정한다. 회귀, 분류문제에서는 주로 p(t∣x),p(C∣x)를 추정한다.
-
그 다음, 분포의 파라미터를 찾는다.
- 빈도주의 방법: 어떤 기준(ex. likelihood)을 최적화시키는 과정을 통해 파라미터 값을 정한다. 파라미터 하나의 값을 구하게 된다.
- 베이지안 방법: 먼저 파라미터의 사전확률을 가정하고 Bayes' rule을 통해 파라미터의 사후확률을 구한다.
-
파라미터를 찾았다면(한 개의 값이든 분포든) 그것을 사용해 "예측"을 할 수 있다(t나 C).
- 켤레사전분포(Conjugate Prior): (베이지안 방법을 사용할 경우) 사후확률이 사전확률과 동일한 함수형태를 가지도록 해준다.
이항변수(Binary Variables): 빈도주의 방법
이항 확률변수(binary random variable) x∈{0,1} (ex. 동전던지기)가 다음을 만족한다고 하자(파라미터화된 분포).
p(x=1∣μ)=μ,p(x=0∣μ)=1−μ
p(x)는 베르누이 분포(Bernoulli distribution)로 표현될 수 있다.
Bern(x∣μ)=μx(1−μ)1−x
- 기댓값, 분산
- E[x]=μ
- var[x]=E[x2]−(E[x])2=μ(1−μ)
우도함수(Likelihood Function)
x값을 N번 관찰한 결과를 D={x1,…,xN}라고 하자. 각 x가 독립적으로 p(x∣μ)에서 뽑혀진다고 가정하면 다음과 같이 우도함수(μ의 함수인)를 만들 수 있다.
p(D∣μ)=∏n=1Np(xn∣μ)=∏n=1Nμxn(1−μ)1−xn
빈도주의 방법에서는 μ값을 이 우도함수를 최대화시키는 값으로 구할 수 있다. 또는 아래와 같이 로그우도함수를 최대화시킬 수도 있다.
lnp(D∣μ)=∑n=1Nlnp(xn∣μ)=∑n=1N{xnlnμ+(1−xn)ln(1−μ)}

μ의 최대우도 추정치(maximum likelihood estimate)는
μML=Nm with m=(#observations of x=1)
N이 작은 경우에 위 MLE는 과적합(overfitting)된 결과를 낳을 수 있다!
N=m=3→μML=1!
이항변수(Binary Variables): 베이지언 방법
이항분포(Binomial Distribution)
D={x1,…,xN}일 때, 이항변수 x가 1인 경우를 m번 관찰할 확률
Bin(m∣N,μ)=(mN)μm(1−μ)N−m
(mN)=(N−m)!m!N!
- 기댓값, 분산
- E[m]=∑m=0NmBin(m∣N,μ)=Nμ
- var[m]=∑m=0N(m−E[m])2Bin(m∣N,μ)=Nμ(1−μ)
베이지안 방법을 쓰기 위해서 데이터의 우도를 구해야 하는데, 이항분포를 가정하면 우도함수가 하나의 변수 m으로(x1,…,xN 대신) 표현가능하므로 간편해진다.
베타분포(Beta Distribution)
베이지언 방법으로 문제를 해결하기 위해 베타분포를 켤레사전분포(conjugate prior)로 사용한다. 베타분포는 μ에 대한 분포임에 유의하자.
Beta(μ∣a,b)=Γ(a)Γ(b)Γ(a+b)μa−1(1−μ)b−1
감마함수 Γ(x)는 다음과 같이 정의된다.
Γ(x)=∫0∞ux−1e−udu
감마함수는 계승(factorial)을 실수로 확장시킨다. Γ(n)=(n−1)!
-
Γ(x)=(x−1)Γ(x−1)
-
a,b값에 따른 베타분포
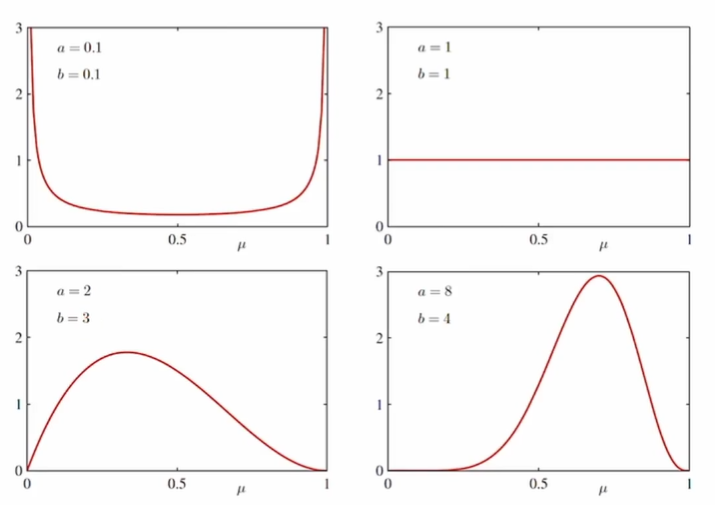
-
기댓값, 분산
- E[μ]=a+ba
- var[μ]=(a+b)2(a+b+1)ab
μ의 사후확률(Posterior)
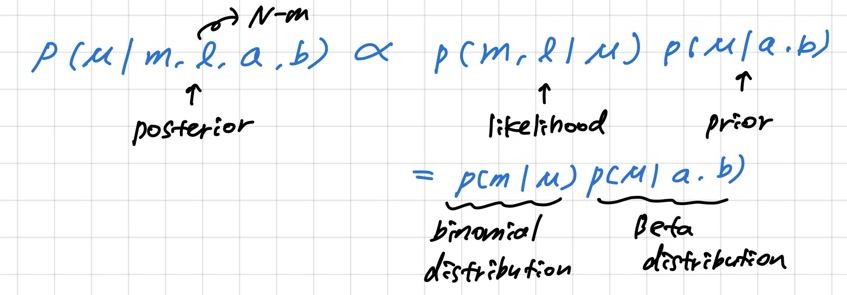
p(μ∣m,l,a,b)=∫01Bin(m∣N,μ)Beta(μ∣a,b)dμBin(m∣N,μ)Beta(μ∣a,b)=∫01μm+b−1(1−μ)l+b−1dμμm+a−1(1−μ)l+b−1=Γ(m+a)Γ(l+b)/Γ(m+a+l+b)μm+a−1(1−μ)l+b−1=Γ(m+a)Γ(l+b)Γ(m+a+l+b)μm+a−1(1−μ)l+b−1
m과 l이라는 관찰이 주어진 후의 사후확률은 a가 m만큼 늘어나고 b가 l만큼 늘어난 효과를 가진다. 새로운 데이터가 들어오면 사후확률을 사전확률로 활용해서 또다시 μ에 대한 지식을 업데이트할 수 있다.
- 연속적인 업데이트: 하나의 샘플을 관찰했을 때, 사전확률과 사후확률의 관계
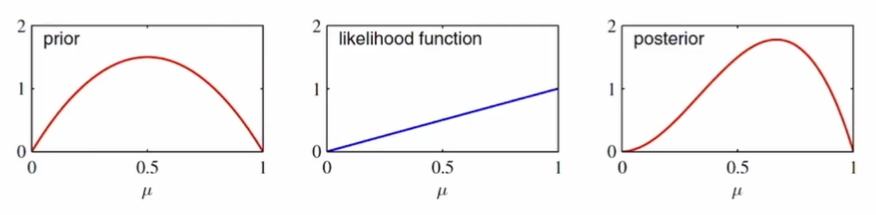
- 첫번째 그림:사전확률은 a=2,b=2인 베타분포
- 두번째 그림: x=1인 하나의 샘플에 대한 우도함수
- 세번째 그림: 사후확률은 a=3,b=2인 베타분포
다음 관찰에 대해선 이 사후확률이 사전확률로 쓰이게 된다.
예측분포(Predictive Distribution)
새로운 데이터 x가 1의 값을 가질 확률?
p(x=1∣D)=∫01p(x=1∣μ)p(μ∣D)dμ=∫01μp(μ∣D)dμ=E[μ∣D]
p(x=1∣D)=m+a+l+bm+a
베이지언 관점은 빈도주의 관점에서 N이 작을경우 나타날 수 있는 극단적인 결과(과적합)를 피할 수 있다. 우리의 사전지식 a,b값이 이를 보정해주기 때문이다.
다항변수(Multinomial Variables): 빈도주의 방법
K개의 상태를 가질 수 있는 확률변수를 K차원의 벡터 x (하나의 원소만 1이고 나머지는 0)로 나타낼 수 있다. 이런 x를 위해서 베르누이 분포를 다음과 같이 일반화시킬 수 있다. p(xk=1∣μμ)=μk
p(x∣μμ)=∏k=1Kμkxk
with ∑kμk=1
- 기댓값
E[x∣μμ]=∑xp(x∣μμ)=(μ1,…,μM)T=μμ
우도함수
x값을 N번 관찰한 결과 D={x1,…,xN}가 주어졌을 때, 우도함수는 다음과 같다.

p(D∣μμ)=∏n=1N∏k=1Kμkxnk=∏k=1Kμk(∑nxnk)=∏k=1Kμkmk
mk=∑nxnk
μ의 최대우도 추정치(maximum likelihood estimate)를 구하기 위해선 μk의 합이 1이 된다는 조건하에서 lnp(D∣μμ)을 최대화시키는 μk를 구해야 한다. 라그랑주 승수(Lagrange multiplier) λ를 사용해서 다음을 최대화시키면 된다.
∑k=1Kmklnμk+λ(∑k=1Kμk−1)
μkML=Nmk
다항변수(Multinomial Variables): 베이지언 방법
다항분포(Multinomial Distribution)
파라미터 μμ와 전체 관찰개수 N이 주어졌을 때 m1,…,mK의 분포를 다항분포(multinomial distribution)이라고 하고 다음과 같은 형태를 가진다.
Mult(m1,…,mK∣μμ,N)=(m1m2…mKN)∏k=1Kμkmk
(m1m2…mKN)=m1!m2!…mK!N!
∑k=1Kmk=N
디리클레 분포(Dirichlet Distribution)
다항분포를 위한 켤레사전분포로, 베타분포를 일반화시킨 형태
Dir(μμ∣α)=Γ(α1)…Γ(αK)Γα0∏k=1Kμkαk−1
α0=∑k=1Kαk
μ의 사후확률(Posterior)
p(μμ∣D,α)=Dir(μμ∣α+m)=Γ(α1+m1)…Γ(αK+mK)Γ(α0+N)k=1∏Kμkαk+mk−1
m=(m1,…,mK)T
αk를 xk=1에 대한 사전관찰 개수라고 생각할 수 있다.





