[TIL Day30] Machine Learning 기초 - Probability Distributions II

아래 내용에 관한 증명은 PRML에서 참고할 수 있다.

가우시안 분포(Gaussian Distribution)

가우시안 분포가 일어나는 여러가지 상황: 정보이론에서 엔트로피를 최대화시키는 확률분포, 중심극한정리

• 단일변수 $x$
  

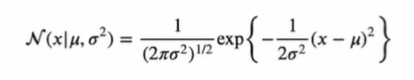
• $D$차원 벡터 $\bold{x}$
  
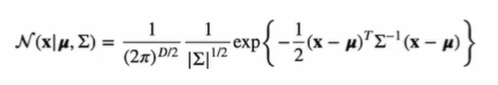
  여기서 $\mu$는 $D$차원의 평균 벡터이고, $\Sigma$는 $D$ x $D$ 크기를 가지는 공분산 행렬이다. 중요한 것은 $\mu$와 $\Sigma$가 평균, 공분산으로 주어진 것이 아니고 이것들이 파라미터로 주어진 확률밀도함수의 평균과 공분산이 $\mu, \Sigma$가 된다는 것이다.

가우시안 분포의 기하학적인 형태

• $\bold{x}$에 대한 함수적 종속성은 지수부에 등장하는 이차형식(quadratic form)에 있다. $\Sigma$가 공분산으로 주어진 것이 아니지만, 이차형식에 나타나는 행렬은 오직 대칭부분만이 그 값에 기여하므로 $\Sigma$가 대칭행렬인 것으로 간주할 수 있다.

• 대칭행렬의 성질에 따라서 $\Sigma$를 아래와 같이 나타낼 수 있다.
  

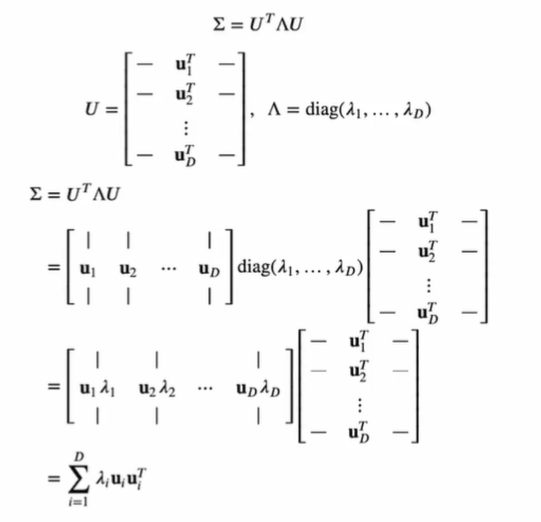
• 이차형식은 다음과 같이 표현될 수 있다.
  

• $\bold{y}$를 벡터들 $\bold u_i$에 의해 정의된 새로운 좌표체계 내의 점으로 해석할 수 있다. 이것을 기저변환(change of basis)이라고 한다.
  - $\bold{x} - \pmb \mu$: standard basis에서의 좌표
  - $\bold{y}$: basis $\{\bold u_1, ... , \bold u_D\}$에서의 좌표
  
  

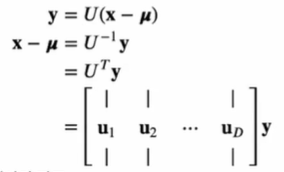
가우시안 분포의 Normalization

• $\bold{y}$의 확률밀도함수
  

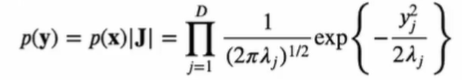
• $\bold{y}$의 normalization
  

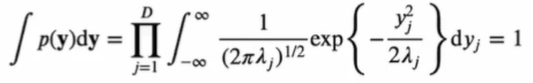
가우시안 분포의 기댓값과 공분산

• 다변량 확률변수의 기댓값
  - $\bold{x} = (x_1, ... , x_n)^T$
  - $\mathbb{E}[\bold{x}] = (\mathbb{E}[x_1], ... , \mathbb{E}[x_n])^T$
  - $\mathbb{E}[x_1] = \int x_1p(x_1)\mathrm{d}x_1 = \int x_1(\int p(x_1, ... , x_n)\mathrm{d}x_2, ..., \mathrm{d}x_n)\mathrm{d}x_1 = \int x_1p(x_1, ... , x_n)\mathrm{d}x_1, ..., \mathrm{d}x_n$

• 가우시안 분포의 기댓값, 공분산
  - $\mathbb{E}[\bold x] = \pmb \mu$
  - $\mathrm{cov}[\bold x] = \Sigma$

조건부 가우시안 분포(Conditional Gaussian Distributions)

두개의 확률 변수의 결합 확률 분포가 가우시안이면, 조건부 확률 분포도 가우시안 분포가 된다. 이 때 두 개의 주변(marginal) 확률 분포도 가우시안 분포가 된다.

즉, $p(\bold{x_a},\bold{x_b})$ 가 가우시안 분포를 따르는 경우, $p(\bold{x_a}|\bold{x_b})$ 도 가우시안 분포를 따르게 된다.

주변 가우시안 분포(Marginal Gaussian Distributions)

• 주변 확률 분포
  - 결합 확률 분포에서 한 쪽의 변수가 사라지거나 무시되는 것
  - $p(x,y)$에서 $x$에 대한 주변 확률 분포는 $p(x)$가 되며, $y$에 대한 주변 확률 분포는 마찬가지로 $p(y)$가 된다.
  - 이산 변수는 모든 확률 값의 합으로, 연속 변수의 경우 적분으로 합산하여 한 쪽의 변수를 사라지게 한다.

• 주변 확률 분포 또한 가우시안 분포가 된다.
  - $\mathbb{E}[\bold x_a] = \pmb \mu_a$
  - $\mathrm{cov}[\bold x_a] = \Sigma_{aa}$