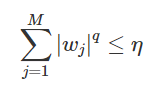[TIL Day31] Machine Learning 기초 - Linear Models for Regression

(작성중)

선형 기저 함수 모델

기저함수(Basis Function)

가장 기본적인 선형 모델 $y(\bold x,\bold w)=w_0+w_1x_1+...+w_Dx_D$ 을 고려하자.
$\bold x=(x_1,…,x_D)^T$ 이고 이 모델의 파라미터는 $\bold w=(w_0,…,w_D)^T$이다. 위 함수는 파라미터 $\bold w$와 입력 데이터 $\bold x$ 모두에 대해서 선형이다.

$\bold x$에 대해 비선형인 함수를 만들고 싶다면, 일반화된 식으로 다음과 같이 표현할 수 있다.
$y(\bold x,\bold w)=w_0+\displaystyle \sum_{j=1}^{M-1}w_jϕ_j(\bold x)$
추가된 함수 $ϕ_j(\bold x)$를 기저함수라고 부르며, 이 함수의 도입으로 기존에는 선형 식이었던 $y(\bold x,\bold w)$ 함수가 $\bold x$에 대해 비선형 함수가 될 수 있다. 그러나 $\bold w$에 대해서는 여전히 선형임을 기억하자.

표기의 편리성을 위해 $ϕ_0(\bold x)=1$ 로 정의하고 좀 더 간략한 식으로 기술하기도 한다.
$y(\bold x,\bold w)=\displaystyle \sum_{j=0}^{M-1}w_jϕ_j(\bold x) = \bold w^Tϕ(\bold x)$

• 다항식 기저함수
  $ϕ_j(x)=x^j$

• 가우시안 기저함수
  $ϕ_j(x)=exp\{− \frac {(x−μ_j)^2}{2s^2}\}$

• 시그모이드 기저함수
  $ϕ_j(x)=σ(\frac {x−μ_j}{s})$
  $σ(a)=\frac {1}{1+exp(−a)}$

최대우도와 최소제곱법(Maximum Likelihood and Least Squares)

에러함수가 가우시안 노이즈를 가정할 때 최대우도로부터 유도될 수 있다는 것을 살펴보았다. 이를 조금 더 자세히 알아보자. 우리가 예측하려고 하는 타겟값 $t$가 다음과 같은 분포를 가진다고 하자.
$t=y(\bold x,\bold w)+\epsilon$

• $y(\bold x,\bold w)$는 결정론적 함수(deterministic)
• $\epsilon$은 가우시안 분포 $N(\epsilon |0,β^{−1})$를 따르는 노이즈 확률변수
• 따라서 t의 분포는 $p(t|\bold x, \bold w, \beta ) = N(t |y(\bold x,\bold w), β^{−1})$

제곱합이 손실함수로 쓰이는 경우, 새로운 $\bold x$가 주어졌을 때 $t$의 최적의 예측값은 $t$의 조건부 기댓값임을 알고있다. $t$가 위의 분포를 따르는 경우 조건부 기댓값은 다음과 같다.
$\mathbb E[t|\bold x] = \int tp(t|\bold x) \mathrm dt = y(\bold x, \bold w)$

파라미터인 $\bold w$를 찾기 위해 최대우도추정법을 사용하자.
입력값은 $\bold X = \bold x_1, ..., \bold x_N$이고 출력값은 $\bold t = t_1, ..., t_N$이다. 로그 우도함수는 다음과 같다.

따라서 로그 우도함수를 최대화시키는 $\bold w$값은 $E_D(\bold w)$로 주어진 제곱합 에러함수를 최소화시키는 값과 동일하다.

위 식을 $\bold w$에 대해 미분하고 좌변을 0으로 두고 풀면 $\bold w$의 최적값을 구할 수 있다.
$\bold w_{ML}=(Φ^TΦ)^{−1}Φ^T\bold t$
위 식을 normal equations라고 부른다. 이 때 사용되는 $Φ$ 는 $N×M$ 크기의 행렬로 디자인 행렬(design matrix) 이라고 한다.

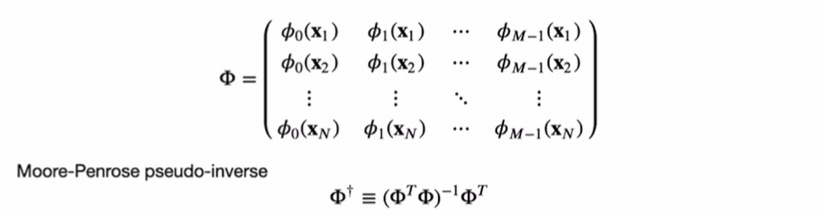
• 편향 파라미터 $w_0$
  $w_0$를 함수에서 분리해 기술한다면 에러 함수가 다음과 같이 변하게 된다.
  
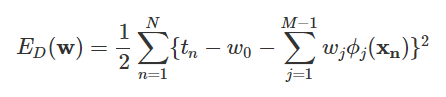
  이 식이 $w_0$로 인해 0이 된다고 하면,
  
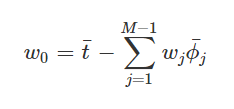
  즉, 에러함수를 최소로 만들어낼 수 있는 $w_0$값의 의미를 살펴보면, 실제 얻어지는 샘플들의 타겟 값들의 평균과 기저함수에 가중치를 곱하여 얻어진 결과의 평균값의 차이를 보정하는 역할을 하게 된다.

• 노이즈 $\beta$의 최적값
  

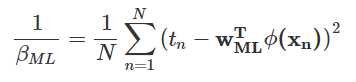
최소 제곱법의 기하학적 의미(Geometry of Least Squares)

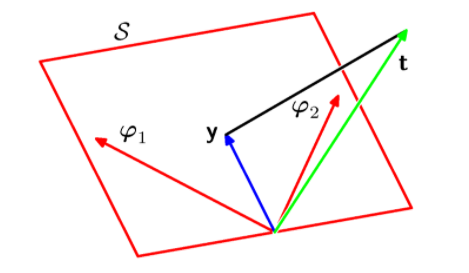
결국 우리가 구하고자 하는 것은 $\bold y$ 벡터가 놓일 수 있는 공간 $S$ 로부터 실제 결과 값 $\bold t$ 벡터 사이에 가장 가까운 거리를 가지는 한 점을 찾는 것이다.

시퀀스 학습 (Sequential learning)

• 배치학습 vs 온라인학습
  전체 데이터를 한번에 사용해서 처리하는 배치학습과는 다르게, 데이터가 순차적으로 입력될 때 모델의 파라미터를 학습하는 방법을 온라인학습(시퀀스학습)이라고 한다. 데이터가 순차적으로 입력됨에 따라서 구해야 할 파라미터 값이 계속해서 갱신되어야 한다.

• Stochastic Gradient Decent
  에러함수를 $E=\sum_nE_n$로 정의하여 파라미터가 업데이트되도록 식을 만들 수 있다.
  
  여기서 $\tau$는 데이터가 반복적으로 입력된 횟수, $η$는 학습률(learning rate) 파라미터이다.

규제화된 최소제곱법(Regularized Least Squares)

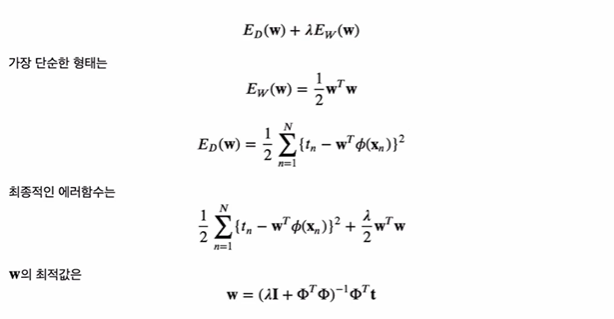
• 일반화된 규제화
  

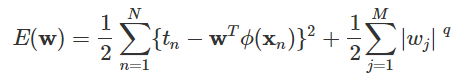
• $q=1$ 인 경우를 Lasso 모델이라고 한다.
  Constrained minimization 문제로 나타낼 수 있다.
  

편향-분산 분해(Bias-Variance Decomposition)

베이지안 선형회귀(Bayesian Linear Regression)