[TIL Day34] 신경망의 기초 - 기계학습과 수학

(작성중)

벡터와 행렬

• 놈(norm)
  - 벡터와 행렬의 거리(크기) 측정
  - 벡터의 p차 놈(p=1; absolute-value norm, p=2; euclidean norm)
  
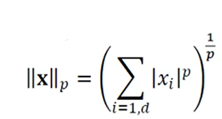
  - 벡터의 최대 놈
  
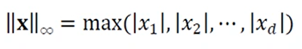
  - 행렬의 프로베니우스 놈
  
  

• 벡터공간
  - 벡터들의 선형결합으로 만들어지는 공간
  - 기저벡터 a와 b의 선형결합 $c = \alpha_1a + \alpha_2b$

역행렬

• 역행렬과 선형 방정식의 해
  - 불능: 해 없음
  - 부정: 다수의 해 존재
  - 유일해 존재: 역행렬을 이용하여 해를 구함
  

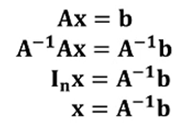
• 서로 필요충분 관계인 조건들
  - $A$는 역행렬을 가진다. 즉, 특이행렬이 아니다.
  - $A$는 최대계수를 가진다.
  - $A$의 모든 행이 선형독립이다.
  - $A$의 모든 열이 선형독립이다.
  - $A$의 행렬식은 0이 아니다.
  - $A^TA$는 양의 정부호 대칭 행렬이다.
  - $A$의 고윳값은 모두 0이 아니다.
  

• 행렬식(determinant)
  
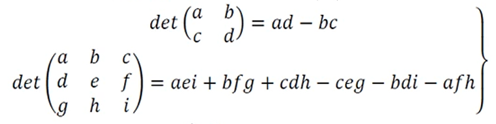
  - 행렬식에 따른 역행렬의 존재 유무
  $det(A)=0$; 역행렬 없음, $det(A)≠0$; 역행렬 존재
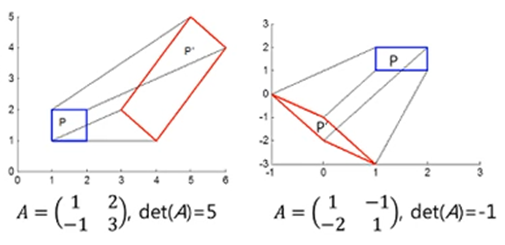
  - 행렬식의 기하학적 의미
  행렬식은 주어진 행렬의 곱에 의한 공간의 확장 또는 축소 해석
  - 만약 $det(A)=0$, 하나의 차원을 따라 축소되어 부피를 잃게 됨
  - 만약 $det(A)=1$, 부피 유지한 변환, 방향 보존됨
  - 만약 $det(A)=-1$, 부피 유지한 변환, 방향 보존 안됨
  - 만약 $det(A)=5$, 5배 부피 확장되며 방향 보존됨
  

• 정부호 행렬
  - 양의 정부호 행렬: 0이 아닌 모든 벡터 $x$에 대해, $x^TAx>0$
  - 성질

  • 고유값이 모두 양수
  • 역행렬도 정부호 행렬
  • $det(A)≠0$ 역행렬 존재

행렬 분해

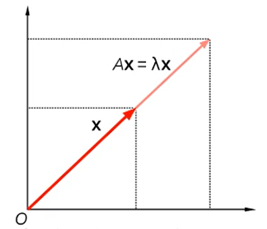
• 고유값과 고유 벡터
  - $Av = \lambda v$: 고유 벡터 $v$와 고유값 $\lambda$
  - 2차원 공간에서의 고유값과 고유 벡터의 기하학적 해석
  
  

• 고유 분해(eigen-decomposition)
  - $A=Q\Lambda Q^{-1}$
  - $Q$는 $A$의 고유 벡터를 열에 배치한 행렬
  - $\Lambda$는 고유값을 대각선에 배치한 대각행렬
  - 고유 분해는 정사각행렬에만 적용 가능
  

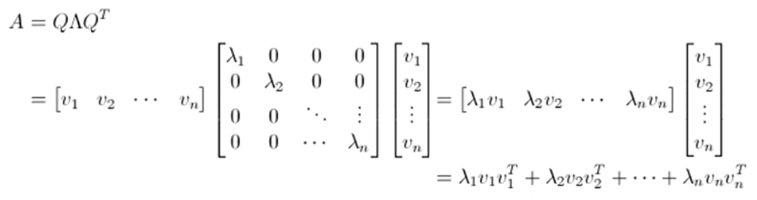
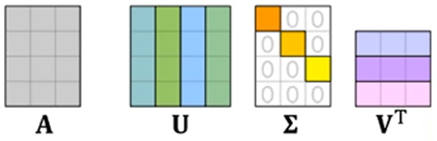
• 특이값 분해(SVD, singular value decomposition)
  - $A=U\Sigma V^T$
  - 왼쪽 특이행렬 $U$: $AA^T$의 고유 벡터를 열에 배치한 $n x n$ 행렬
  - 오른쪽 특이행렬 $V$: $A^TA$의 고유 벡터를 열에 배치한 $m x m$ 행렬
  - $\Sigma$: $AA^T$의 고윳값의 제곱근을 대각선에 배치한 $n x m$ 대각행렬
  
  - 정사각행렬이 아닌 행렬의 역행렬 계산에 사용
  
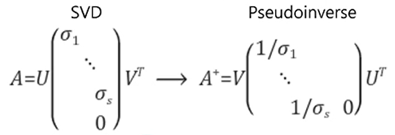
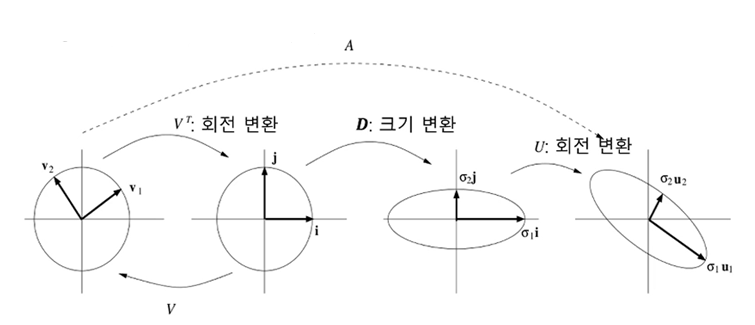
  - 기하학적 해석
  
  

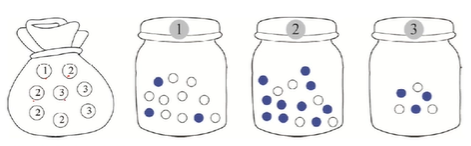
확률 기초

간단한 확률실험 장치를 고려하자. 주머니에서 번호를 뽑은 다음, 번호에 따라 해당 병에서 공을 뽑고 색을 관찰한다. 번호를 $y$, 공의 색을 $x$라는 확률변수로 표현하면 정의역은 $y∈\{1, 2, 3\}, x∈\{blue, white\}$

곱 규칙과 합 규칙

• 곱 규칙
  

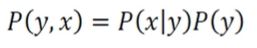
• 조건부 확률에 의한 결합확률 계산
  번호는 1번, 공은 하얀 공일 확률
  = $P(y=1, x=white)=P(x=white|y=1)P(y=1)$

• 합 규칙
  

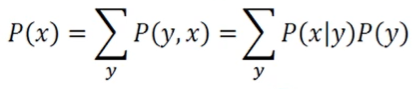
• 합 규칙과 곱 규칙에 의한 주변확률 계산
  하얀 공이 뽑힐 확률
  $P(white)=P(white|1)P(1) + P(white|2)P(2) + P(white|3)P(3)$

용어 및 정의

• 조건부 확률
  
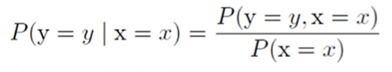
• 확률의 연쇄 법칙
  
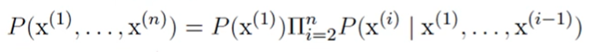
• 독립
  
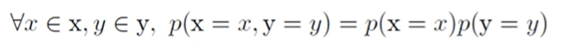
• 조건부 독립
  
• 기대값
  
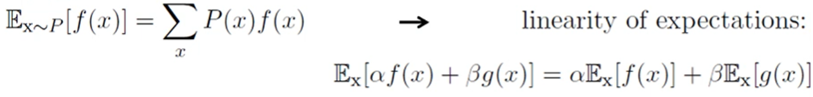
• 평균과 분산
  
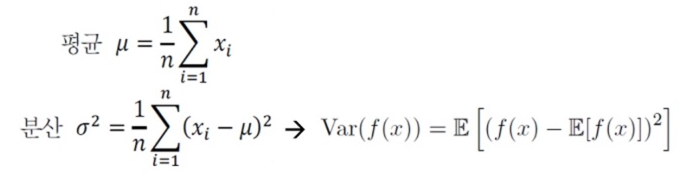
• 공분산행렬(확률변수의 상관정도)
  

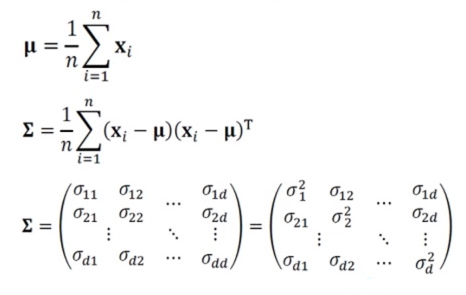
최대 우도

어떤 확률변수의 관찰된 값들을 토대로 그 확률변수의 매개변수(모수)를 구하는 방법
"데이터 x가 주어졌을 때, x를 발생시켰을 가능성을 최대로 하는 매개변수의 값을 찾아라"

• 최대 우도 추정
  
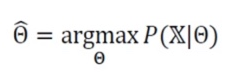
• 최대 로그우도 추정
  

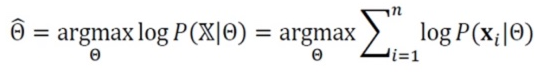
베이즈 정리와 기계 학습

• 베이즈 정리
• 적용 예시
• 베이즈 정리의 해석
• 기계 학습에 적용

정보이론

• 자기 정보
• 엔트로피
• 교차 엔트로피
• KL 다이버전스
• 교차 엔트로피와 KL 다이버전스의 관계

최적화

• 기계 학습 최적화
• 학습 모델의 매개변수 공간
• 미분에 의한 최적화
• 행렬의 미분
  - 야코비언 행렬
  - 헤세 행렬
  

경사 하강 알고리즘

• 배치 경사 하강 알고리즘(BGD)
• 확률론적 경사 하강 알고리즘(SGD)