[TIL Day35] 신경망의 기초 - 다층퍼셉트론 I

인공신경망

• 사람의 신경망과 인공신경망 비교

  사람 신경망	인공 신경망
  세포체	노드
  수상돌기	입력
  축삭	출력
  시냅스	가중치

• 신경망의 종류
  - 전방 신경망과 순환 신경망
  - 얕은 신경망과 깊은 신경망
  - 결정론적 신경망과 확률론적 신경망
  • 결정론적 신경망: 모델의 매개변수와 조건에 의해 출력이 완전히 결정
  • 확률론적 신경망: 고유의 임의성을 가지고 매개변수와 조건이 같더라도 다른 출력을 가짐

퍼셉트론

절(node), 가중치(weight), 층(layer)과 같은 새로운 개념의 구조 도입, 학습 알고리즘 제안

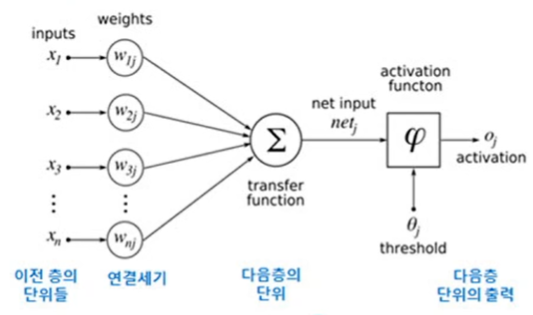
퍼셉트론의 구조

• 입력
  - i번째 노드는 특징 벡터 $\bold{x}=(x_1, x_2, ..., x_d)^T$의 요소 $x_i$를 담당
  - 항상 1이 입력되는 편향(bias)(임계값을 구분하는 계단 함수를 0점에서부터 비교할 수 있도록 만드는 역할) 노드를 포함
  

• 연산
  - $i$번째 입력 노드와 출력 노드를 연결하는 변(edge)은 가중치 $w_i$를 가짐
  - 퍼셉트론은 단일 층 구조라고 간주

• 출력
  - 한 개의 노드에 의해 수치(+1 혹은 -1) 출력
  

• 퍼셉트론의 동작
  - 선형 연산 → 비선형 연산
  - 선형: 입력(특징)값과 가중치를 곱하고 모두 더해 $s$(스칼라)를 구함
  - 비선형: 활성함수 $\tau$를 적용
  - 활성함수로 계단 함수를 사용 → 출력 $y=+1$ 혹은 $y=-1$
  
  

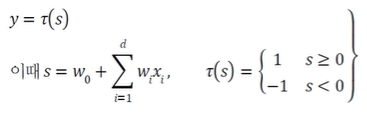
기하학적 의미

• 결정 직선
  - $d(\bold{x}) = d(x_1, x_2) = w_1x_1 + w_2x_2 + w_0=0 → x_1+x_2-0.5=0$
  - $w_1, w_2$는 직선의 기울기, $w_0$은 절편(편향)을 결정
  - 결정 직선은 특징 공간을 +1과 -1의 두 부분공간으로 이분할하는 분류기 역할
  
  
• $d$차원 공간으로 일반화
  - $d(\bold{x}) = w_1x_1 + w_2x_2 + ... + w_dx_d + w_0=0$
  - 2차원: 결정 직선, 3차원: 결정 평면, 4차원 이상: 결정 초평면
  

학습

• 일반적인 분류기의 학습 과정
  - 단계 1: 과업의 정의와 분류 과정의 수학적 정의(가설 설정)
  - 단계 2: 해당 분류기의 목적함수 $J(\theta)$ 정의
  - 단계 3: $J(\theta)$를 최소화하는 \theta를 찾기 위한 최적화 방법 수행

• 목적함수 정의
  - 퍼셉트론의 매개변수를 $\bold{w} = (w_0, w_1, w_2, ..., w_d)^T$라 표기하면, 매개변수 집합은 $\theta = \{\bold{w}\}$
  - 목적함수를 $J(\theta)$ 또는 $J(\bold{w})$로 표기

• 퍼셉트론 목적함수의 상세 조건
  - $J(\bold{w}) >= 0$이다.
  - $\bold{w}$가 최적이면, 즉 모든 샘플을 맞히면 $J(\bold{w}) = 0$이다.
  - 틀리는 샘플이 많은 $\bold{w}$일수록 $J(\bold{w})$는 큰 값을 가진다.
  

• 목적함수 상세 설계
  
  - 임의의 샘플 $\bold{x}_k$가 $Y$에 속한다면, 퍼셉트론의 예측 값 $\bold{w}^T\bold{x}_k$와 실제 값 $y_k$는 부호가 다르므로 $-y_k(\bold{w}^T\bold{x}_k)$는 항상 양수
  - 결국 $Y$가 클수록(틀린 샘플이 많을수록), $J(\bold{w})$는 큰 값을 가짐
  - $Y$가 공집합일 때(즉 퍼셉트론이 모든 샘플을 맞출 때), $J(\bold{w})=0$
  

경사 하강법

최소 $J(\theta)$ 기울기를 이용하여 반복 탐색하여 극값을 찾음

• 경사도 계산
  - 일반화된 가중치 갱신 규칙 $\theta=\theta-\rho \bold{g}$를 적용하려면 경사도 $\bold{g}$가 필요
  
  
  

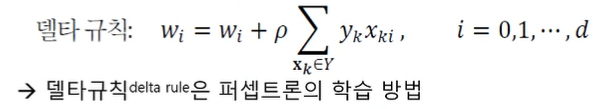
퍼셉트론 학습 알고리즘

• stochastic ver.
  

• batch ver.
  훈련집합의 샘플을 모두 맞출 때까지 세대(epoch)를 반복(3~9번째 줄)