[TIL Day40] 신경망의 기초 - 심층학습 최적화 I

목적함수

평균제곱오차

$e = 1/2||y-o||_2^2$
오차가 클수록 $e$값이 크므로 정량적 성능으로 활용된다.
하지만, 신경망 학습 과정에서 MSE가 더 커서 큰 교정이 필요함에도 오류 역전파 시 작은 경사도로 작게 갱신되는 경우가 있다.

로지스틱 시그모이드 함수와 그 도함수를 살펴보면, $wx + b$가 커지면 경사도가 작아지는 문제가 있기 때문.

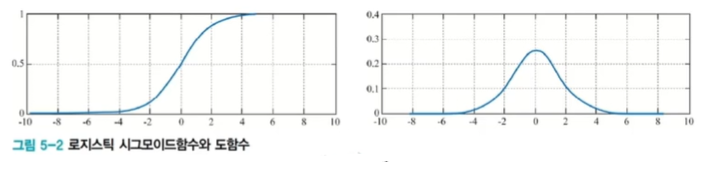
교차 엔트로피 목적함수

정답에 해당하는 y를 확률변수로 두고 $P$는 정답 확률 분포, $Q$는 신경망 (예측) 출력 확률 분포라고 하자.
$P(0) = 1-y$
$P(1) = y$
$Q(0) = 1-o$
$Q(1)=o$ (신경망 출력으로 표기하면, $o=\sigma(z)$ 이고 $z=wx+b$)

교차 엔트로피는 다음과 같이 쓸 수 있다.
$H(P, Q) = -\Sigma_{y∈\{0,1\}}P(y)log_2Q(y)$

• 교차 엔트로피 목적함수
  $e = -(ylog_2o + (1-y)log_2(1-o)$

• 공정한 벌점을 부여하는지 확인해보자(MSE의 느린 학습 문제를 해결하는지)
  - 도함수
  

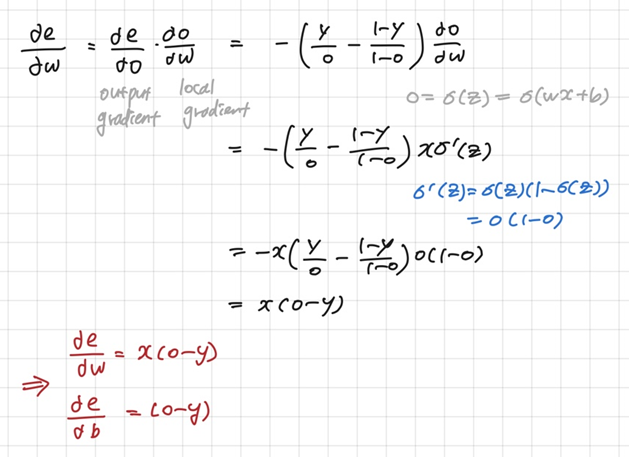
  • 경사도를 계산해보면, 오류가 더 큰 쪽에 더 큰 벌점(경사도)을 부과하는 것을 확인할 수 있다.

• $c$개의 출력 노드를 가진 경우로 확장
  - 출력 벡터 $o=(o_1, o_2, ..., 0_c)^T$인 상황으로 확장
  
  

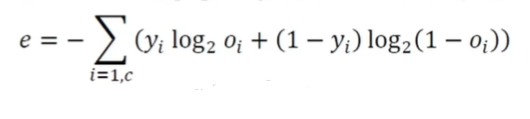
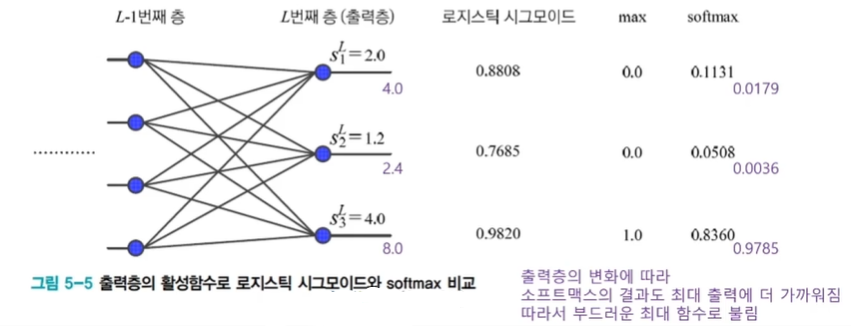
소프트맥스 함수와 로그우도 목적함수

• 소프트맥스(softmax) 함수
  
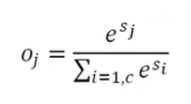
  - exponential 함수는 음의 무한대부터 양의 무한대까지 모든 범위를 양수로 만들어주는 효과
  - 최대(max)를 모방
  - 출력 노드의 중간 계산 결과 $s_i^L$의 최댓값을 더욱 활성화하고 다른 작은 값들은 억제
  - 모두 더하면 1이 되어 확률 모방
  
  

• 음의 로그우도 목적함수
  
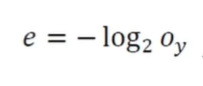
  - 모든 출력 노드값을 사용하는 MSE나 교차 엔트로피와 달리 $o_y$라는 하나의 노드에만 적용
  - $o_y$는 샘플의 정답에 해당하는 노드의 출력값
  - 정답값을 잘못 예측하였다면 $o_y$가 작을 것이고, 이는 목적함수(손실함수)를 크게 만듦

• 소프트맥스와 로그우도
  - 소프트맥스는 최댓값이 아닌 값을 억제하여 0에 가깝게 만든다는 의도 내포
  - 신경망에 의한 샘플의 정답에 해당하는 노드만 보겠다는 로그우도와 잘 어울림
  - 둘을 결합하여 사용하는 경우가 많음
  

성능 향상을 위한 요령

데이터 전처리

• 규모(scale) 문제

• 모든 특징이 양수인 경우의 문제
  - 가중치가 뭉치로 증감하면 최저점을 찾아가는 경로가 갈팡질팡하여 느린 수렴

• 정규화(normalization)
  - 규모 문제와 양수 문제를 해결
  - 특징별 독립적으로 적용
  - 정규 분포를 활용한 표준화 변환(평균이 0, 표준편차가 1이 되도록 변환)
  
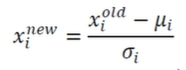
  - 최대 최소 변환(0~1사이의 범위로 변환)
  

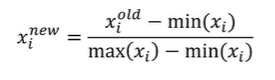
• 명목 변수를 원핫 코드로 변환
  - 명목 변수: 객체간 서로 구분하기 위한 변수로, 거리 개념이 없음
  - 원핫 코드는 값의 개수만큼 비트(bit)를 부여
  

가중치 초기화

• 대칭적 가중치 문제
  - 같은 값으로 갱신되어 두 노드가 같은 일을 하는 중복 발생
  - 난수로 초기화함으로써 대칭 파괴

• 난수로 가중치 초기화
  - 가우시안 혹은 균일 분포에서 난수 추출, 두 분포는 성능 차이 거의 없음
  - 난수의 범위는 무척 중요!
  - 아래 식으로 $r$을 결정한 후 $[-r, r]$사이에서 난수 발생
  ($n_{in}$은 노드로 들어오는 에지 개수, $n_{out}$은 노드에서 나가는 에지 개수)
  
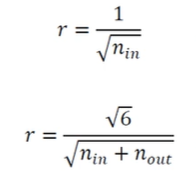
  - 편향은 보통 0으로 초기화

탄력(가속도, 관성)

• 경사도의 잡음 현상
  - 훈련집합을 이용하여 매개변수의 경사도를 추정하므로 잡음 가능성
  - 탄력(momentum)은 경사도에 부드러움을 가하여 잡음 효과 줄임
  - 관성(가속도): 과거에 이동했던 방식을 기억하면서 기존 방향으로 일정 이상 추가 이동
  - 수렴 속도 향상(local minima, saddle point에 빠지는 문제 해소)

• 관성을 적용한 가중치 갱신
  
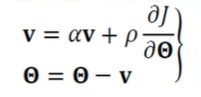
  - 속도 벡터 $v$: 이전 경사도를 누적한 것에 해당(처음 $v=0$로 출발)
  - $\alpha$의 효과(관성의 정도)

  • $\alpha=0$이면 관성이 적용 안된 이전 경사도 갱신 공식과 동일
  • $\alpha$가 1에 가까울수록 이전 경사도 정보에 큰 가중치를 주는 것으로 $\theta$가 그리는 궤적이 매끄러움
  • 보통 0.5, 0.9, 0.99등을 사용
    

• 네스테로프 가속 경사도 관성
  

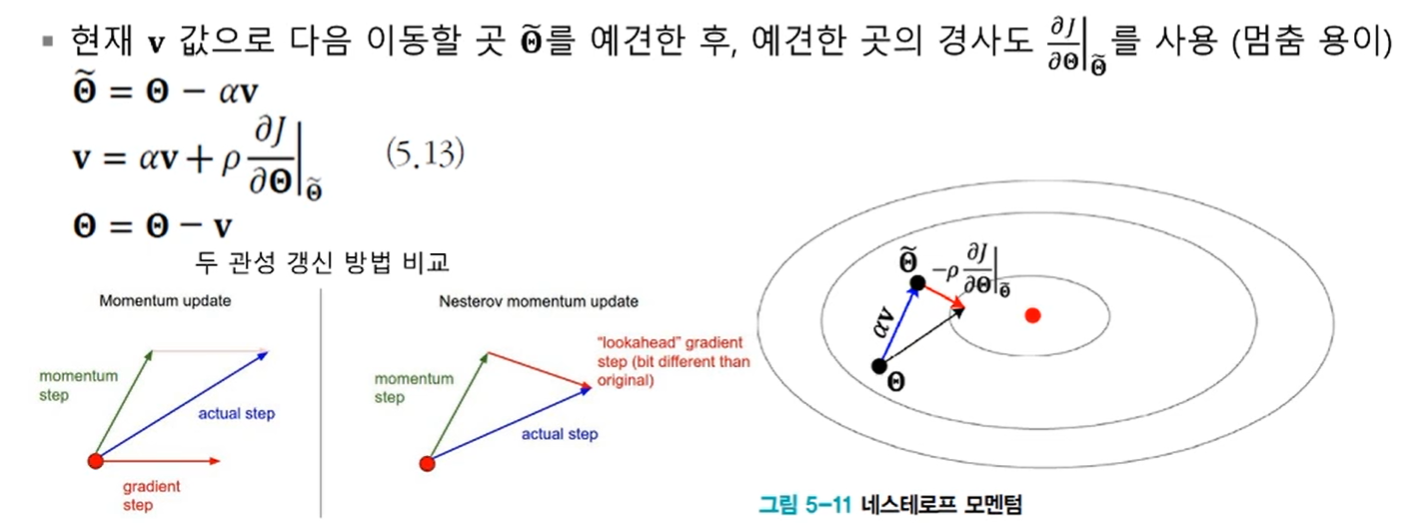
적응적 학습률

• 학습률의 중요성
  - 너무 크면 지나침에 따른 진자 현상
  - 너무 작으면 수렴이 느림

• 적응적 학습률(adaptive learning rates)
  - 기존 경사도 갱신은 모든 매개변수에 같은 크기의 학습률을 사용하는 셈
  - 적응적 학습률은 매개변수마다 자신의 상황에 따라 학습률을 조절해 사용
  - ex) 학습률 담금질(stimulated annealing)

  • 이전 경사도와 현재 경사도의 부호가 같은 매개변수는 값을 키우고 다른 매개변수는 값을 줄이는 전략