[TIL Day41] 신경망의 기초 - 심층학습 최적화 II

이다혜·2021년 6월 30일

TIL

목록 보기

42/60

성능 향상을 위한 요령

활성함수

선형 연산 결과인 활성값 $z$ 에 비선형 활성함수 $\tau$ 를 적용하는 과정

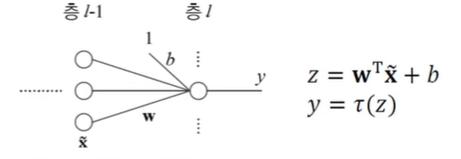
ReLU(Rectified Linear Unit) 활성함수
- 경사도 포화(gradient saturation) 문제 해소
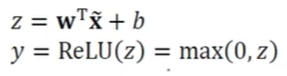
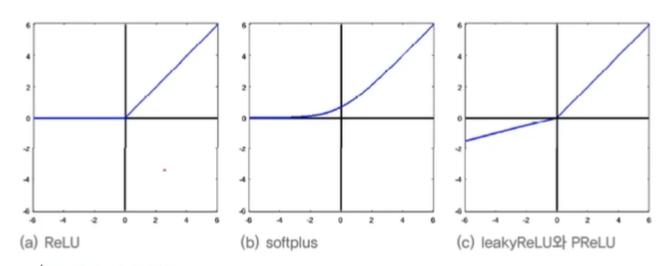
ReLU의 변형
- gradient가 0이 되어 한 번 deactivated 된 부분은 계속 탐색되지 않는 문제를 극복
- Leaky ReLU (보통 $\alpha=0.01$ 사용)

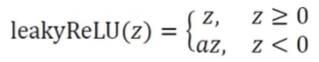
- Parametric ReLU ( $\alpha$ 를 학습으로 알아냄)

배치 정규화

공변량 변화 현상

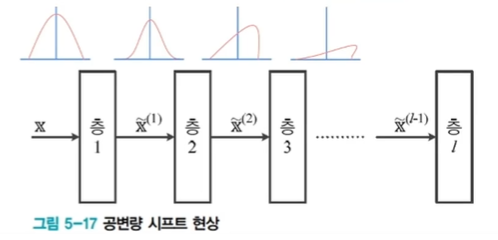
- 훈련집합과 테스트집합의 분포가 다름
- 딥러닝 모델 내부의 공변량 변화
- 학습이 진행되면서 첫번째 층의 매개변수가 바뀜에 따라 그 층의 output 분포가 바뀌고, 두번째 층 입장에서 보면 자신에게 입력되는 데이터의 분포가 수시로 바뀌는 셈
- 층이 깊어짐에 따라 더욱 심화되어 학습을 방해하는 요인으로 작용
배치 정규화

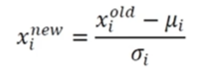
- 공변량 시프트 현상을 누그러뜨리기 위해 정규화를 층 단위 적용하는 기법
- 정규화를 적용하는 위치가 중요! 일반적으로 완전연결층, 합성곱층 후에 혹은 비선형 함수(활성함수) 전에 적용
- 훈련집합 전체가 아닌 미니배치에 적용하는 것이 유리
배치 정규화 과정

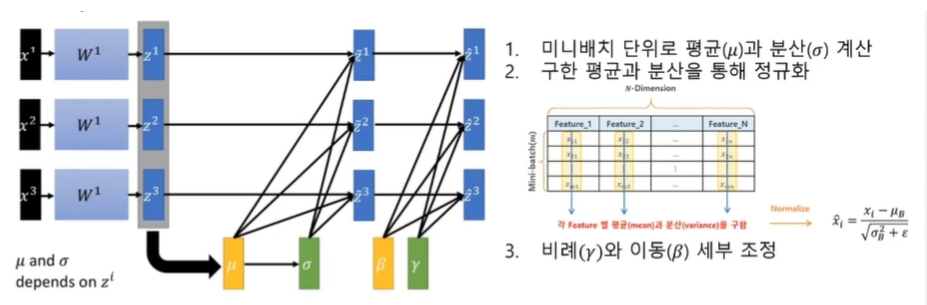
- 데이터 전처리 과정에서의 정규화와 다른 점
- 비례( $\gamma$ )와 이동( $\beta$ ) 세부 조정
- $\gamma$ 와 $\beta$ 는 노드마다 고유한 매개변수로서, 학습으로 알아냄
장점
- 신경망의 경사도 흐름 개선
- 높은 학습률 허용
- 초기화에 대한 의존성 감소
- 규제와 유사한 행동을 하며, 드롭아웃의 필요성 감소시킴
(학습이 끝난 후) 예측 단계
- 전체 훈련집합에 대해 $\mu, \sigma^2$ 를 구함
- 학습을 통해 얻은 $\gamma, \beta$ 와 함께 아래 식 적용
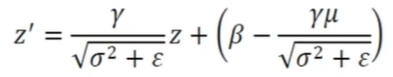
CNN에서는 노드 단위가 아니라 특징 맵 단위로 적용
- 특징 맵의 크기가 pxq라면, 미니배치(크기 m)에 있는 샘플마다 pg개의 값이 발생
- 총 pgm개의 값을 가지고 $\mu_B$ 와 $\sigma_B^2$ 를 계산
- $\gamma$ 와 $\beta$ 는 특징 맵마다 하나씩 존재

규제

일반화 오류를 줄이려는 의도를 가지고 학습 알고리즘을 수정하는 방법

과잉적합에 빠지는 이유

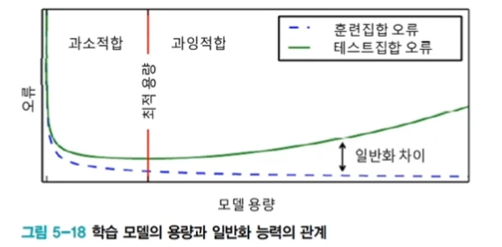
- 대부분 가지고 있는 데이터에 비해 훨씬 큰 용량의 모델을 사용
- 훈련 집합을 단순히 암기하는 과잉적합에 주의해야
- 현대 기계학습의 전략은, 충분히 큰 용량의 모델을 설계한 다음 "학습 과정에서" 여러 규제 기법을 적용
규제의 정의
- 모델 용량에 비해 데이터가 부족한 경우의 부족조건문제를 푸는 접근법
- "입력과 출력 사이의 변환은 매끄럽다"는 사전 지식(가정)을 투입하여 문제를 품
- 규제항에 추가적으로 만족하길 원하는 조건을 포함시키자
- 대표적인 티호노프의 규제 기법
본 문제: $Ax = b$
관점 변환: $||Ax - b||_2^2$ 최소화
규제를 적용한 문제: $||Ax-b||_2^2 + ||\Gamma x||_2^2$

명시적 규제와 암시적 규제
- 명시적 규제: 가중치 감쇠, 드롭아웃 등 목적함수나 신경망 구조를 직접 수정
- 암시적 규제: 조기 멈춤, 데이터 증대, 잡음 추가, 앙상블 등 간접적 영향

규제 기법

1. 가중치 벌칙
규제항을 큰 가중치에 벌칙을 가해 작은 가중치를 유지하기 위해 적용, 주로 $L2 norm$ (ridge regression)이나 $L1 norm$ (lasso regression)을 사용

가중치 감쇠(weight decay)
- 규제항 $R$ 로 $L2 norm$ 을 사용하는 규제 기법

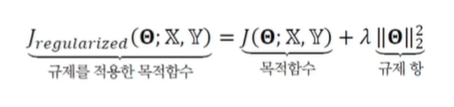
- 매개변수를 갱신하는 수식

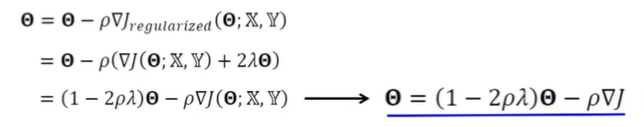
- 가중치 감쇠는 $\theta$ 에 $(1-2\rho\lambda)$ 를 곱해주는 셈
- 최종해를 원점 가까이 당기는 효과가 있음, 즉 가중치를 작게 유지
효과
- 가중치에 대한 선호도 표현( $\lambda$ 값으로 조절)
- 학습 모델을 단순화시킴으로 일반화 성능 향상
- 매끄럽게 하여 최적화 개선

2. 조기 멈춤
일정 학습 시간이 지나면 과잉적합 현상이 나타나 일반화 능력이 저하된다. 즉, 훈련 데이터를 단순히 암기하기 시작하는 것. 조기 멈춤은 검증집합의 오류가 최저인 점에서 학습을 멈추는 규제 기법.

참을성(duration)을 반영
- 일정 횟수 이상 연속적으로 성능 향상이 없으면 학습을 멈춤
- 설익은 수렴 방지

3. 데이터 확대
과잉적합을 방지하는 가장 확실한 방법은 큰 훈련집합을 사용하는 것. 데이터를 인위적으로 변형하여 데이터를 확대해 사용하자. 이동, 회전, 반전, 자르기, 노이즈 추가, 색상 변환 등을 적용할 수 있다.

4. 드롭아웃
완전연결층의 노드 중 일정 비율(일반적으로 p=0.5)을 임의 선택하여 제거하는 규제 기법으로, 많은 부분 신경망을 만들고 앙상블 결합하여 사용할 수 있다.

적용 방법
- 참거짓 배열 $\pi$ 로 노드 제거 여부를 표시
- $\pi$ 는 (미니배치) 샘플마다 독립적으로 정함, 난수로 설정
- 일반적으로 입력층 제거 비율 $p_{input}=0.2$ , 은닉층 제거 비율 $p_{hidden}=0.5$ 로 설정
예측 단계
- 학습 과정에서 가중치가 (1-드롭아웃 비율 $p$ )만큼만 참여했기 때문에 $p$ 만큼 보정 필요

5. 앙상블 기법
서로 다른 여러 개의 모델을 결합하여 일반화 오류를 줄이는 기법

서로 다른 예측기를 학습
- 서로 다른 구조의 신경망 여러개를 학습, 또는 같은 구조를 사용하지만 서로 다른 초기값과 하이퍼 매개변수를 설정하고 학습
- 배깅: 훈련 집합을 여러 번 샘플링하여 서로 다른 훈련집합을 구성
- 부스팅: i번째 예측기가 틀린 샘플을 i+1번째 예측기가 잘 인식하도록 연계성 고려
학습된 예측기를 결합
- 모델 평균
- 여러 모델의 출력에서 평균을 구하거나 투표하여 최종 결과 결정