순차 데이터
순차 데이터의 표현
-
순차 데이터의 일반적 표기
- 벡터의 벡터(벡터의 요소가 벡터)
- 훈련집합
,
- 각 샘플(여기서 와 는 1대1 대응되지 않을 수 있다)
, -
대표적인 순차 데이터, 문자열의 표현: 사전 사용
- 사전 구축 방법: 사람이 사용하는 단어를 모아 구축 또는 주어진 말뭉치를 분석하여 단어를 자동 추출하여 구축
- 사전을 사용한 텍스트 순차 데이터의 표현 방법- 단어가방(BoW; Bag of Words)
단어 각각의 빈도수를 세어 m차원의 벡터로 표현(m은 사전 크기)하는 방식으로, 시간성 정보는 반영하지 못하는 한계가 있음 - 원핫코드(one-hot code)
해당 단어의 위치만 1로 표시하는 방식으로, 한 단어를 표현하는데 m차원 벡터를 표현하는 비효율성을 가지며 단어 간 유사성을 측정할 수 없음 - 단어 임베딩(word embedding)
단어 사이의 상호작용을 분석하여 새로운 공간으로 변환(m보다 훨씬 낮은 차원)하는 방식으로, 변환 과정은 학습이 말뭉치를 훈련집합으로 사용하여 알아냄
- 단어가방(BoW; Bag of Words)
순차 데이터의 특성
- 특징이 나타나는 순서가 중요
- 순서가 바뀌면 의미가 크게 훼손됨
- 샘플마다 길이가 다름
- 순환 신경망은 은닉층에 순환 연결을 부여하여 가변 길이 수용
- 문맥 의존성
- 비순차 데이터는 공분산이 특징 사이의 의존성을 나타냄
- 순차 데이터에서는 공분산은 의미가 없고, 대신 문맥 의존성이 중요
- 중요 문맥(특징) 간 간격이 클 경우 '장기 의존성'이라 부름(LSTM으로 처리)
순환 신경망(RNN)
- 순환 신경망이 갖추어야 할 세 가지 필수 기능!
- 시간성: 특징을 순서대로 한번에 하나씩 입력
- 가변 길이: 길이가 T인 샘플을 처리하려면 은닉층이 T번 나타나야 함(T는 가변적)
- 문맥 의존성: 이전 특징 내용을 기억하고 있다가 적절한 순간에 활용
구조
기존의 깊은 신경망과 유사하게 입력층, 은닉층, 출력층이 있으나 다른 점은 은닉층이 순환 연결을 가진다는 점!
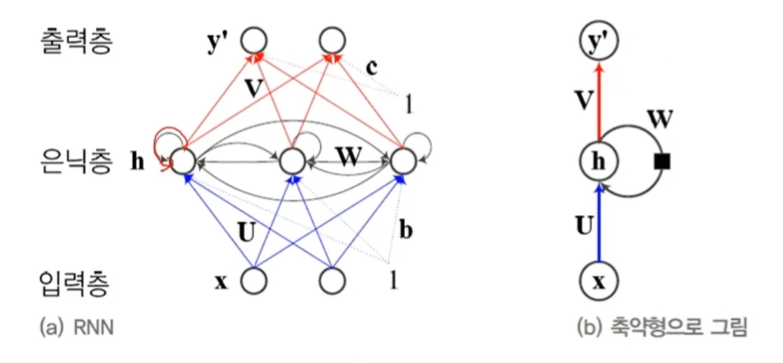
-
은닉층의 순환 연결
- 시간성, 가변 길이, 문맥 의존성을 모두 처리할 수 있음
- 순환 연결은 t-1 순간에 발생한 정보를 t 순간으로 전달하는 역할 -
수식적으로 살펴보자
- 순간에 계산, 그 결과를 가지고 순간에 계산, ... 순간까지 반복
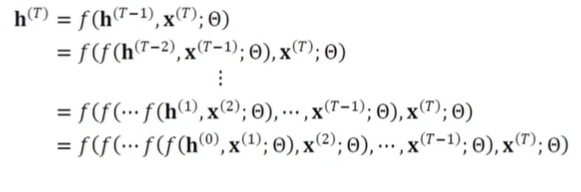
- 일반적으로 순간에는 순간에 은닉층 값(상태) 와 t순간의 입력 를 받아 로 전환 -
순환 신경망의 매개변수
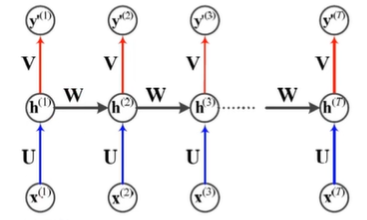
- 가중치 집합
- 는 입력층과 은닉층을 연결하는 pxd행렬
- 는 은닉층과 은닉층을 연결하는 pxp행렬
- 는 은닉층과 출력층을 연결하는 qxp행렬
- 는 바이어스로서 각각 px1과 qx1행렬 -
매개변수 공유
- 매 순간 다른 값을 사용하지 않고 같은 값을 공유함
- 추정할 매개변수 수가 획기적으로 줄어듦
- 매개변수의 수가 특징 벡터의 길이 에 무관
- 특징이 나타나는 순간이 뒤바뀌어도 같더나 유사한 출력을 만들 수 있음
동작
-
은닉층의 계산
,
이때,
(순간의 입력에서 를 곱하고, 이전 층에서 나온 에 를 곱함) -
출력층의 계산
BPTT학습
back propagation through "time"
-
RNN과 DMLP의 차별성
- RNN은 샘플마다 은닉층의 수가 다름(얼마나 전달될 수 있는지에 따라)
- DMLP는 왼쪽에 입력, 오른쪽에 출력이 있지만 RNN은 매 순간 입력과 출력이 있음
- RNN은 가중치를 공유 -
목적함수의 정의
- 출력값을 , 목푯값을 으로 표기
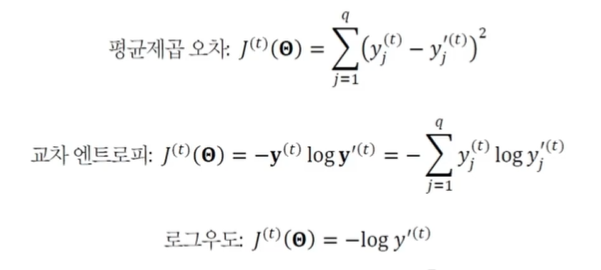
- 학습이 할 일

-
경사도 계산()
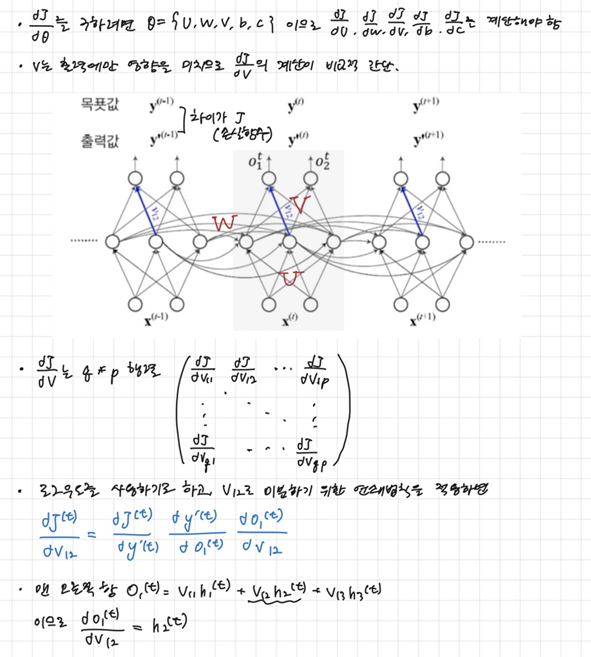
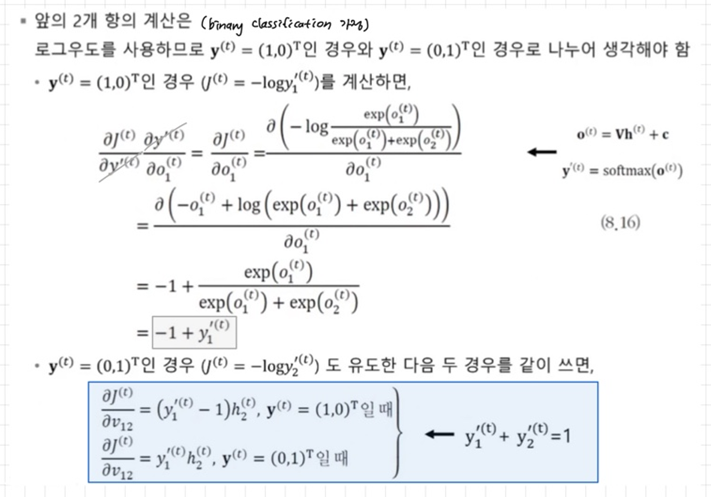

-
BPTT 알고리즘
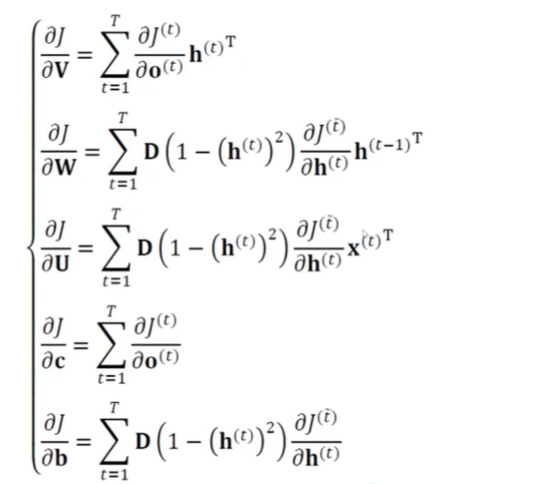
양방향 RNN
- Bidirectional RNN
- 왼쪽에서 오른쪽으로만 정보가 흐르는 단방향 RNN은 한계가 있음
- 이를 극복하기 위해 t순간의 단어는 앞쪽 단어와 뒤쪽 단어 정보를 모두 보고 처리되도록 함
- 기계번역에서도 BRNN 활용
