집합론

Remarks.정칙 공리는 다음과 동치$$\\exists x \\in X : x \\cap X = \\varnothing$$(\*)로 표시된 공리는 분류 공리꼴로부터 유도할 수 있다.(\*\*)로 표시된 공리는 치환 공리꼴로부터 유도할 수 있다.분류 공리꼴의 내용은 “

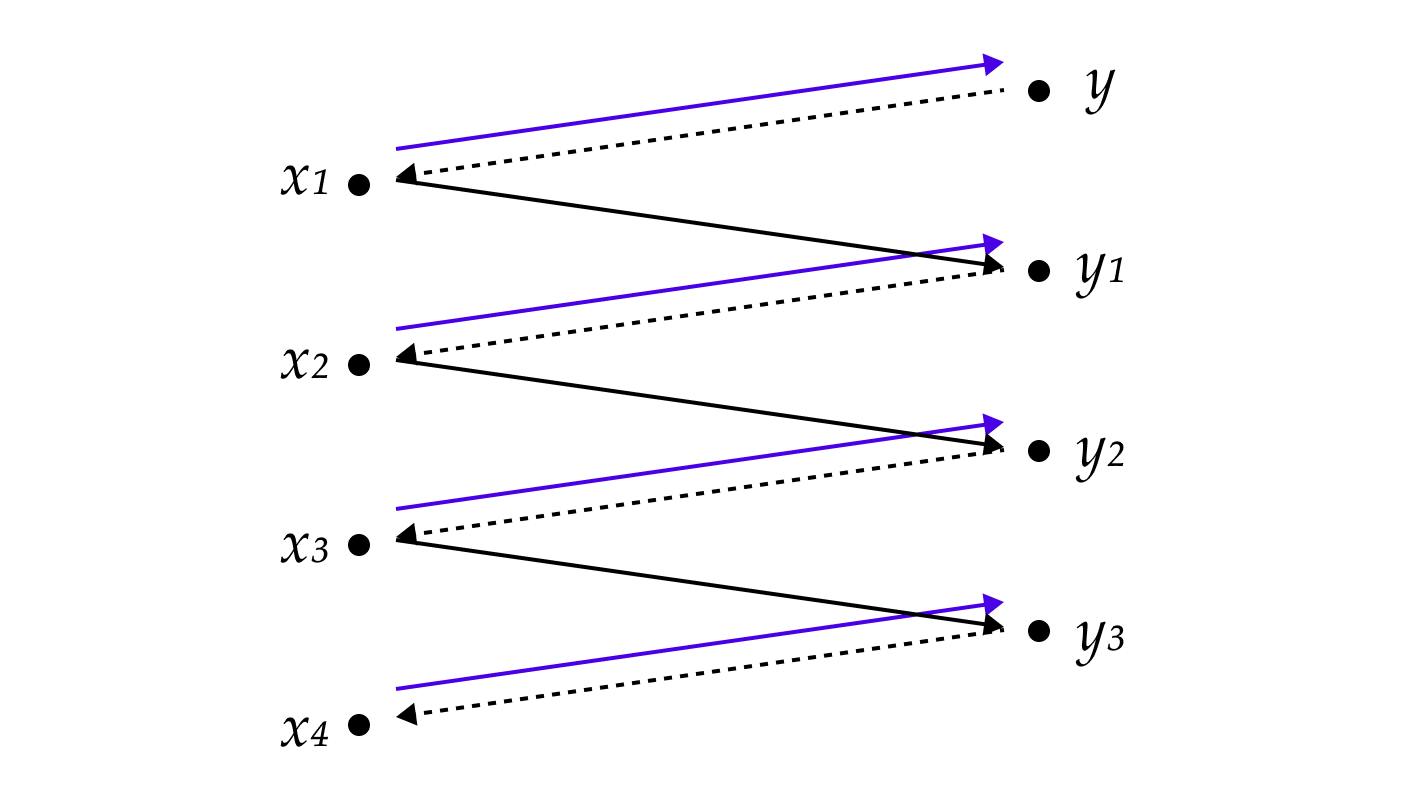
정리. 두 집합 $A, B$에 대해 $|A| \\leq |B|$, $|A| \\geq |B|$라면 $|A| = |B|$이다.매우 당연해 보이지만 $\\leq$가 단사함수의 존재성으로, $=$가 전단사함수의 존재성으로 정의된다는 점에서 트리키한 함수 핸들링을 요구한다.여

칸토어의 동형성 정리 | 데데킨트 절단 | 완비화 정리

1. 기본 개념 > 정의. 다음을 만족하는 $(W, > 1. $(W, 2. $W$의 임의의 부분집합은 최소 원소를 가진다. > > 정의. $(W, 정리. $S$가 정렬 집합 $(W, $$ > S = W[a] \coloneqq \{ x \in W : x $$

정리. $P$가 서수 위에서 정의된 속성이고 임의의 $\\alpha \\in \\mathrm{Ord}$에 대해$$ \\forall \\beta < \\alpha : P(\\beta) → P(\\alpha)$$가 성립할 때, $P$는 모든 서수에 대해 참이다. Re

1. 전체 1.1. 폰 노이만 전체 초한귀납적으로 $\{ V_\alpha \}$를 정의하자. $V_0 = \varnothing$ $V{\alpha + 1} = V\alpha \cup \mathcal{P}(V_\alpha)$ $\lambda$가 극한 서수일 때, $