5. Actor-Critic Algorithm

Advanced Policy Gradient

Progress beyond Vanilla Policy Gradient

• Natural Policy Gradient: REINFORCE
• PPO (Proximal Policy Optimization)
• TRPO (Trust Region Policy Optimization)

Basic idea in on-policy optimization

training performace를 무너뜨리는 taking bad actions의 경우를 피하자

• PPO
  • line search : first pick direction, then step size
• TRPO
  • trust region : first pick step size, then direction

둘이 opposite한 방식 사용
PPO가 stable

Improving the policy gradient: Lowering Variance

trajectory가 적을수록 variance는 높아짐

$\bigtriangledown_\theta J(\theta) \approx \frac{1}{N}\underset{i=1}{\overset{N}{\sum}}\underset{t=1}{T}\bigtriangledown_\theta \log\pi_\theta(a_{i,t}|s_{i,t})\big(\underset{t'=1}{\overset{T}{\sum}}r(s_{i.t'}. a_{i.t'})\big)$
뒤에 $-avg(r)$을 더하기도 함
N=number of trajectory

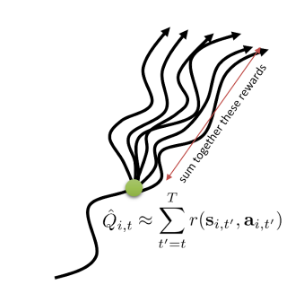
• $\big(\underset{t'=1}{\overset{T}{\sum}}r(s_{i.t'}. a_{i.t'})\big) = \hat{Q}_{i,t}$ : reward to go
  • state $s_{i,t}$에서 action $a_{i.t}$를 취할 경우의 expected reward 추정값

$s_t$에서 할 수 있는 action이 다양하기 때문에 여러 시나리오(trajectory)가 존재함

can we get a better estimate?

• $Q(s_t.a_t) = \sum_{t'=t}^{T}E_{\pi_\theta}[r(s_{t'}. a_{t'}) | s_t.a_t]$ : true expected reward-to-go
  $\hat{Q}$를 $Q$로 바꾸어 모든 trajectory를 고려하도록 함

$\rightarrow \bigtriangledown_\theta J(\theta) \approx \frac{1}{N}\underset{i=1}{\overset{N}{\sum}}\underset{t=1}{T}\bigtriangledown_\theta \log\pi_\theta(a_{i,t}|s_{i,t})Q(s_{i,t},a_{i,t})$

Baseline Trick: Lowering Variance

위의 식에서 reward가 언제나 양수면 학습을 잘 못하기 때문에, $Q-V$로 변경
$\rightarrow \bigtriangledown_\theta J(\theta) \approx \frac{1}{N}\underset{i=1}{\overset{N}{\sum}}\underset{t=1}{T}\bigtriangledown_\theta \log\pi_\theta(a_{i,t}|s_{i,t})(Q(s_{i,t},a_{i,t})-V(s_{i,t}))$

• $Q(s_{i,t},a_{i,t})-V(s_{i,t})$ : Advantage function
• $Q(s_{i,t},a_{i,t})$ : 모든 시나리오의 reward 평균
• $V(s_{i,t})$ : b(=baseline)
  lower the variance를 통해 학습이 더 stable할 수 있도록 함

$b_t = \frac{1}{N}\underset{i}{\sum}Q(s_{i,t},a_{i,t})$
$V(s_t) = E_{a_t\sim \pi_\theta(a_t|s_t)}\big[Q(s_t,a_t)\big]$
$= V^\pi(s_t) = \underset{t'=t}{\overset{T}{\sum}}E_{\pi_\theta}[r(s_{t'},a_{t'})|s_{t'}]$

이때, baseline은 trajectory에 따라 다름(depend on state)
state가 action보다 reward에 영향 大
→ 다양한 action에 대해 평균 내서 구함

State & State-action Value Function

• $Q^\pi(s_t,a_t) = \underset{t'=t}{\overset{T}{\sum}}E_{\pi_\theta}[r(s_{t'}, a_{t'})|s_t,a_t]$ : total reward from taking $a_t$ in $s_t$
• $V^\pi(s_t) = \underset{t'=t}{\overset{T}{\sum}}E_{\pi_\theta}[r(s_{t'},a_{t'})|s_{t'}]$ : total reward from $s_t$
• $A^\pi(s_t,a_t) = Q^\pi(s_t,a_t)-V^\pi(s_t)$ : how much better $a_t$ is
• $\bigtriangledown_\theta J(\theta) \approx\frac{1}{N}\underset{i=1}{\overset{N}{\sum}}\underset{t=1}{\overset{T}{\sum}}\bigtriangledown_\theta(a_{i,t}|s_{i,t})A^\pi(s_{i,t},a_{i,t})$

다양한 trajectory를 사용하기 때문에,
the better this estimate, the lower the variance
그러나 sample에 따라 미분값이 달라지는 biased 발생

policy gradient와의 비교

$\bigtriangledown_\theta J(\theta) \approx\frac{1}{N}\underset{i=1}{\overset{N}{\sum}}\underset{t=1}{\overset{T}{\sum}}\bigtriangledown_\theta(a_{i,t}|s_{i,t})\big(\underset{t'=1}{\overset{T}{\sum}}r(s_{i,t'},a_{i,t'}-b)\big)$

b에 따라 미분값에 변화가 없기 때문에 unbiased
but high variance single-sample estimate

Value Function Fitting

무엇을 fit해야 되냐면...

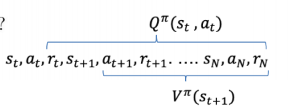
이에 따라서
$Q^\pi(s_t,a_t) = r(s_t,a_t)+V^\pi(s_{t+1})$

$\rightarrow A^\pi(s_t,a_t)=Q^\pi(s_t,a_t)-V^\pi(s_t) \\\quad\quad\quad\quad\quad\space\space= r(s_t,a_t)+V^\pi(s_{t+1}) - V^\pi(s_t)$

$\Rightarrow\space V^\pi(s)$만 fit하면 됨

Policy Evaluation

$V^\pi(s_t) = \underset{t'=t}{\overset{T}{\sum}}E_{\pi_\theta}[r(s_{t'},a_{t'}|s_t)]$
$J(\theta) = E_{s_1\approx p(s_1)}\big[V^\pi(s_1)\big]$

여기서 policy evaluation은 Monte Carlo policy evaluation을 통해 함
what policy gradient does

• $V^\pi(s_t)\approx\underset{t'=t}{\overset{T}{\sum}}r(s_{t'},a_{t'})$
• $V^\pi(s_t) \approx\frac{1}{N}\underset{i=1}{\overset{N}{\sum}}\underset{t'=t}{\overset{T}{\sum}}r(s_{t'},a_{t'})$

다양한 초기 조건을 통해 더 일반적인 추정치를 얻기 위해 시뮬레이터를 여러 번 초기화

추정의 신뢰성을 높이기 위해 많은 trajectory를 생성해야 하므로, 시뮬레이터를 reset해서 여러 에피소드를 독립적으로 진행

Monte Carlo evaluation with function approximation

$V^\pi(s_t)\approx\underset{t'=t}{\overset{T}{\sum}}r(s_{t'},a_{t'})$ 은 $V^\pi(s_t) \approx\frac{1}{N}\underset{i=1}{\overset{N}{\sum}}\underset{t'=t}{\overset{T}{\sum}}$ 만큼 좋지는 않음

but still pretty good!

• training data: ${(s_{i,t},\sum_{t'=t}^{T}r(s_{i,t'},a_{i,t'}))}$ $\quad\sum_{t'=t}^{T}r(s_{i,t'},a_{i,t'}) : y_{i,t}$

• supervised regression: $L(\phi) = \frac{1}{2}\underset{i}{\sum}\Vert\hat{V}_\phi^\pi(s_i)-y_i\Vert^2$

Can we do better?

• ideal target
  $y_{i,t} = \underset{t'=t}{\overset{T}{\sum}}E_{\pi_\theta}r(s_{t'},a_{t'}|s_{i,t})\approx r(s_{i,t},a_{i,t})+V^\pi(s_{i,t+1})\approx r(s_{i,t},a_{i,t})+\hat{V}_\phi^\pi(s_{i,t+1})$

• Monte carlo target
  $y_{i,t}=\underset{t'=t}{\overset{T}{\sum}}r(a_{i,t'},a_{i,t'})$

• training data
  ${(s_{i,t},r(s_{i,t},a_i,t)+\hat{V}_\phi^\pi(s_{i,t+1}))}$

  • $\hat{V}_\phi^\pi(s_{i,t+1})$ might incorrect
  • $r(s_{i,t},a_{i,t})+\hat{V}_\phi^\pi(s_{i,t+1}) = y_{i,t}$

• supervised regression
  $L(\phi) = \frac{1}{2}\underset{i}{\sum}\Vert\hat{V}_\phi^\pi(s_i)-y_i\Vert^2$

sometimes referred to as a "bootstrapped" estimate
low variance, high bias

이해가 안 돼서 gpt한테 물어봤는데

• Low Variance:
  bootstrapped target $r(s_{i,t},a_{i,t})+\hat{V}_\phi^\pi(s_{i,t+1})$는 다음 상태의 가치 함수 추정치를 사용해 평균적인 변동성을 줄이므로 Monte Carlo 방식보다 variance가 낮아 학습이 안정적
• High Bias:
  target이 미래 상태에 대한 추정치에 기반하므로, 초기에는 부정확한 추정치가 누적될 가능성이 있음. 이는 이상적인 target보다 낮은 수준의 정확도를 제공하게 되어 편향이 발생 가능

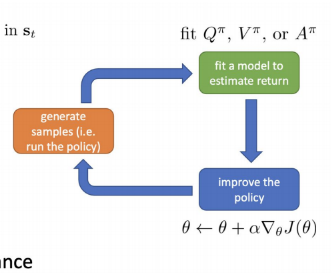
From Evaluation to Actor Critic

An actor-critic algorithm

batch actor-critic algorithm

1. sample ${s_i,a_i}$ from $\pi_\theta(a|s)$ (run it on the robot)
2. fit $\hat{V}_\phi^\pi(s)$ to sampled reward sums
3. evaluate $\hat{A}^\pi(s_i,a_i) = r(s_i,a_i)+\hat{V}_\phi^\pi(s_i')-\hat{V}_\phi^\pi(s_i)$
   $s_i' = s_{i+1}$
4. $\bigtriangledown_\theta J(\theta)\approx\underset{i}{\sum}\bigtriangledown_\theta\log\pi_\theta(a_i|s_i)\hat{A}^\pi(s_i,a_i)$
5. $\theta\leftarrow\theta+\alpha\bigtriangledown_\theta J(\theta)$

이때,

• $y_{i,t} = r(s_{i,t},a_{i,t})+\hat{V}_\phi^\pi(s_{i,t+1})$
• $L(\phi) = \frac{1}{2}\underset{i}{\sum}\Vert\hat{V}_\phi^\pi(s_i)-y_i\Vert^2$
  알고리즘에 optimize는 policy를 하는 거고, $V$는 이 loss function을 이용해 optimize함

on-policy에서 기원한 알고리즘이라 trajectory를 모두 꺼내고 다음을 진행해야 함 $\rightarrow$ 시간이 오래 걸리고 비효율적

Putting Discount Factors

T(episode length)가 $\infty$인 경우,
$\hat{V}_\phi^\pi$ can get infinitely large in many cases

simple trick: better to get reward sooner than later

$y_{i,t} \approx r(s_{i,t},a_{i,t}) + \gamma\hat{V}_\phi^\pi(s_{i,t+1})$

여기서 $\gamma \in [0,1]$ : discount factor 0.99 works well

$A^\pi(s_t,a_t) = Q^\pi(s_t,a_t)-V^\pi(s_t) \\=r(s_t,a_t)+V^\pi(s_{t+1})-V^\pi(s_t) \\\approx r(s_t,a_t)+\gamma V^\pi(s_{t+1})-V^\pi(s_t)$

Actor-critic algorithm (with discount)

batch actor-critic algorithm

1. sample ${s_i,a_i}$ from $\pi_\theta(a|s)$ (run it on the robot)
2. fit $\hat{V}_\phi^\pi(s)$ to sampled reward sums
3. evaluate $\hat{A}^\pi(s_i,a_i) = r(s_i,a_i)+\gamma\hat{V}_\phi^\pi(s_i')-\hat{V}_\phi^\pi(s_i)$
   $s_i' = s_{i+1}$
4. $\bigtriangledown_\theta J(\theta)\approx\underset{i}{\sum}\bigtriangledown_\theta\log\pi_\theta(a_i|s_i)\hat{A}^\pi(s_i,a_i)$
5. $\theta\leftarrow\theta+\alpha\bigtriangledown_\theta J(\theta)$

online actor-critic algorithm

bootstrapping한 알고리즘

1. take action $a\sim \pi_\theta(a|s)$, get $(s,a,s',r)$
2. update $\hat{V}_\phi^\pi$ using target $r+\gamma\hat{V}_\phi^\pi(s')$
3. evaluate $\hat{A}^\pi(s_i,a_i) = r(s_i,a_i)+\gamma\hat{V}_\phi^\pi(s_i')-\hat{V}_\phi^\pi(s_i)$
   $s_i' = s_{i+1}$
4. $\bigtriangledown_\theta J(\theta)\approx\underset{i}{\sum}\bigtriangledown_\theta\log\pi_\theta(a_i|s_i)\hat{A}^\pi(s_i,a_i)$
5. $\theta\leftarrow\theta+\alpha\bigtriangledown_\theta J(\theta)$

한 timestep에서만 trajectory를 뽑을 수 있게 되어 sampling efficent해짐
one transition($s_t,a_t,r_t$)만 가지고 와서 학습이 가능해짐