[Deep Learning] Chapter 2 - Machine Learning Basics

이한량·2025년 4월 8일

목록 보기

1/10

Machine Learning

과거 AI는 인간에게는 어렵지만 컴퓨터에게는 쉬운 문제를 주로 다루도록 설계되었던 반면, 현대 AI는 직관적이지만 표현하기 어려운 문제(Easy to Human, Hard to Computer)를 다루도록 설계되고 있다.

Machine Learning(기계 학습)이란 다음과 같이 정의할 수 있다.

어떤 프로그램이 특정한 작업 $T$ 에 대한 경험 $E$ 를 통해 성능 측정 기준 $P$ 에 따른 성능이 향상된다면 그 프로그램은 "학습했다"고 부를 수 있다.

즉, 기계의 학습은 어떤 작업을 잘 할 수 있는 능력을 얻는 과정 정도로 이해할 수 있다.

Task

Task $(T)$ 란, 기계가 해결해야 하는 어떠한 작업을 의미한다.

기계를 학습시키는 방식은 다음과 같이 나눌 수 있다.

Supervised Learning (지도 학습) : 정답(Label)을 제공하여 학습을 진행
- Classification (분류) : 입력에 대한 이산적인 정답을 예측
- Regression (회귀) : 입력에 대한 연속적인 정답을 예측
Unsupervised Learning (비지도 학습) : 정답(Label)을 제공하지 않고 학습을 진행 $\rarr$ 데이터에 숨겨져 있는 유용한 정보를 발견할 수 있음
- Clustering (군집화) : 원본 데이터들을 그룹화
Reinforcement Learning (강화 학습) : 정답을 맞출 경우 얻을 수 있는 보상을 최대화하는 방향으로 학습을 진행

Experience

Experience $(E)$ 란, 모델이 학습에 사용하는 데이터(Data Set)를 의미한다.

어떤 데이터를 학습에 사용하기 위해선 데이터를 구조화해야 한다.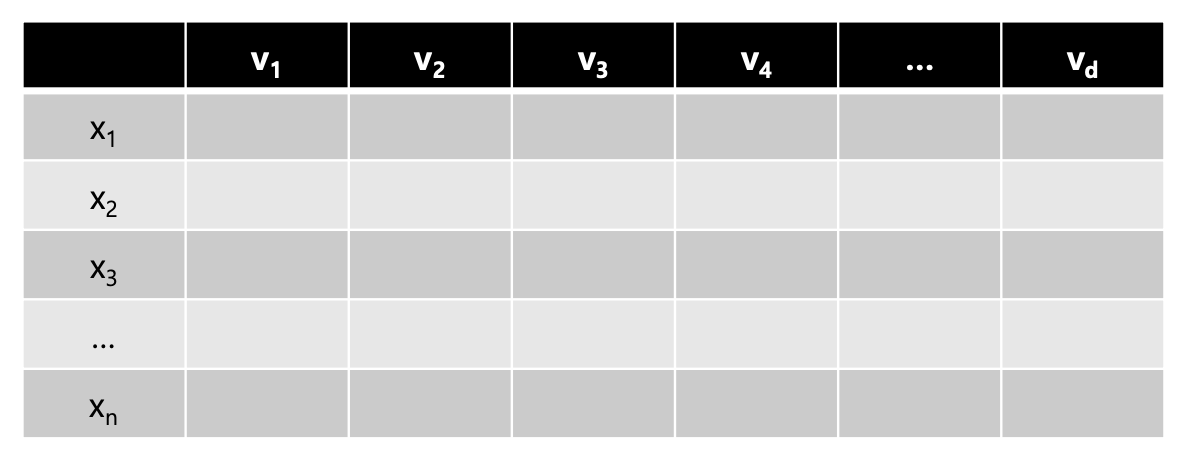

Performance

Performance $(P)$ 란, 모델이 Task를 얼마나 잘 수행하고 있는지 평가하기 위한 수치적 지표를 의미한다.

Classification(분류) 문제에서 활용하는 대표적인 평가 지표들을 살펴보자.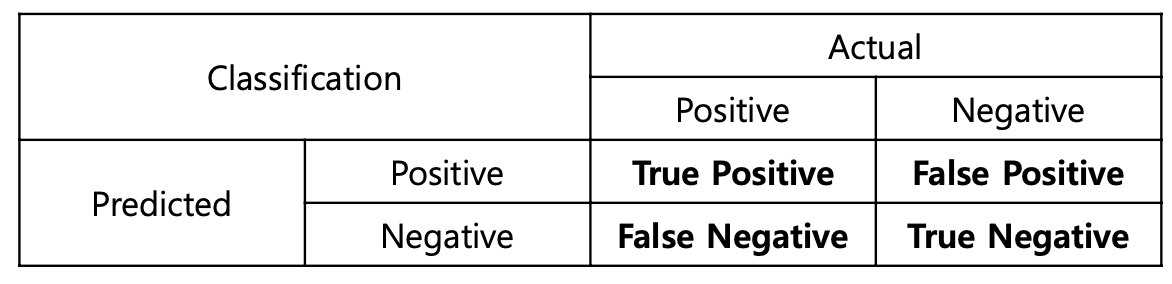

Accuracy : $\frac{TP + TN}{TP+FP+FN+TN}$
Precision : $\frac{TP}{TP+FP}$
Recall (Sensitivity, True positive rate, Hit ratio) : $\frac{TP}{TP+FN}$
Specificity (True negative rate) : $\frac{TN}{TN+FP}$
False alarm (False positive rate) : $\frac{FP}{TN+FP} = 1-specificity$
F1-score : $2\times\frac{precision\times recall}{precision + recall}$

Foundation Model

다양한 Task에 활용이 가능하도록 대규모 데이터셋으로 사전 학습된 모델을 Foundation Model이라고 한다.

Foundation Model은 Self-supervised Learning이 가능하다.

(Contrastive Learning)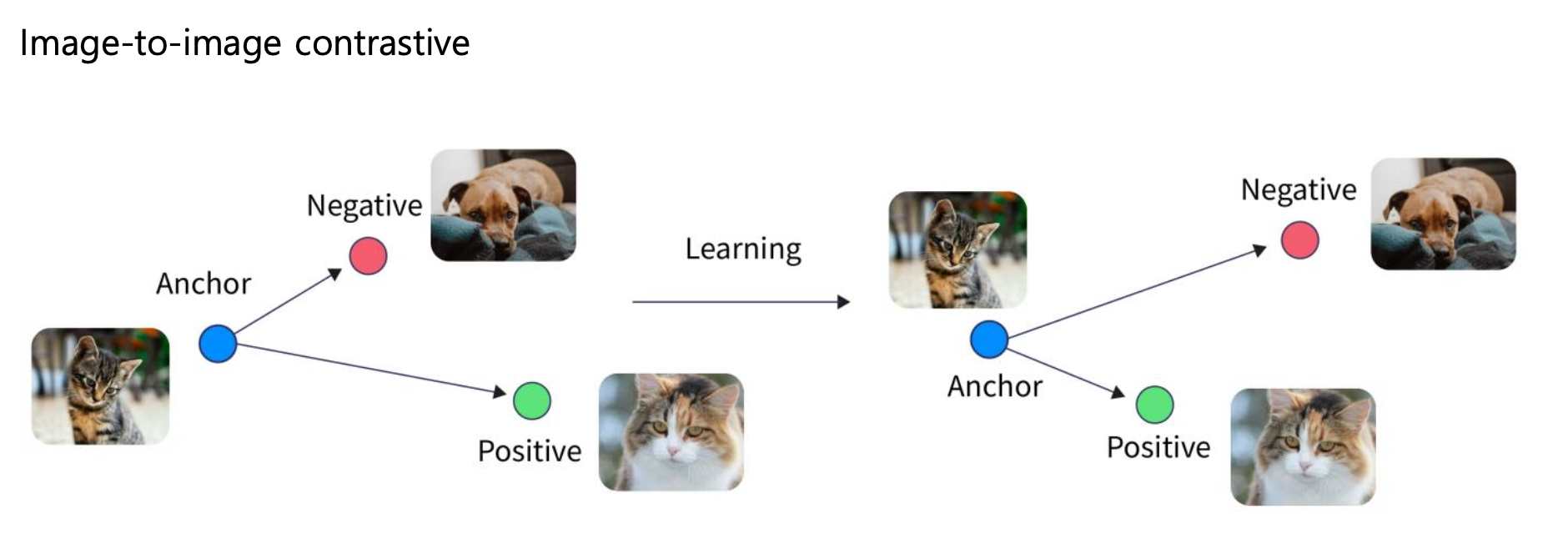

(Generation-based Method)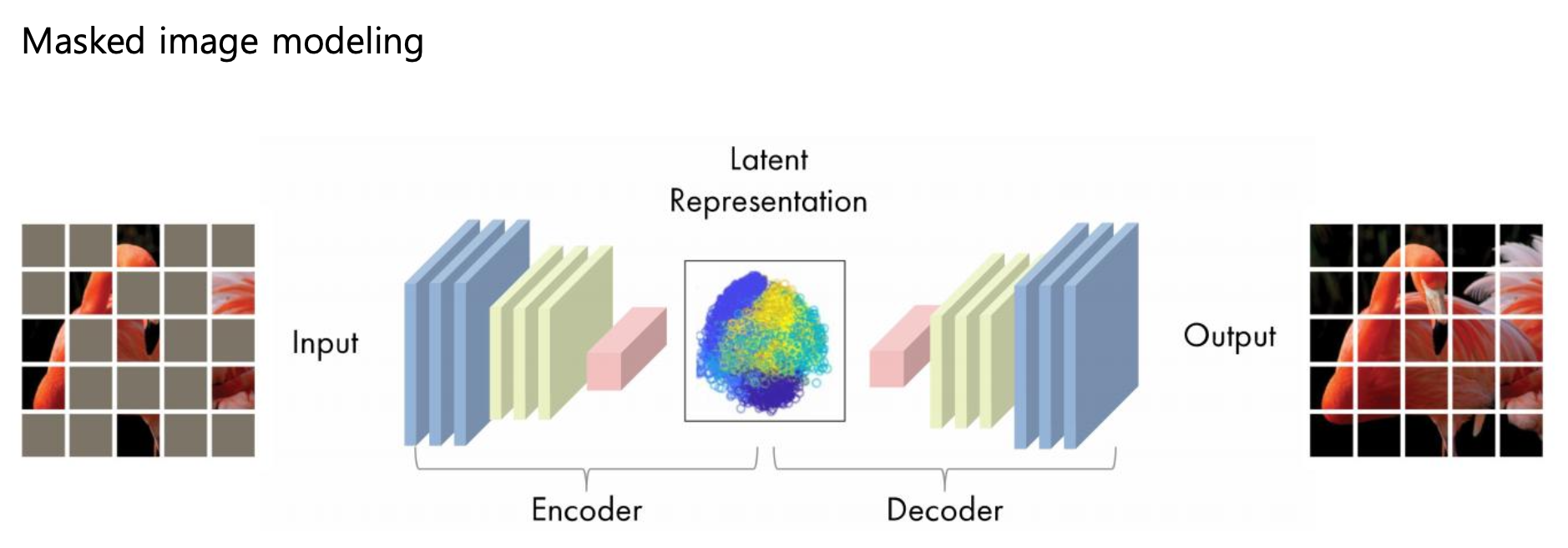

Dataset

세상에 존재하는 모든 데이터를 학습에 활용한다는 것은 현실적으로 불가능하다.

따라서 기계학습의 목표는 학습에 사용되지 않은 데이터셋에 대한 예측 성능을 높이는 것이다.

즉, Generalization(일반화) 성능이 높은 모델을 생성하는 것이 기계학습의 목표이다.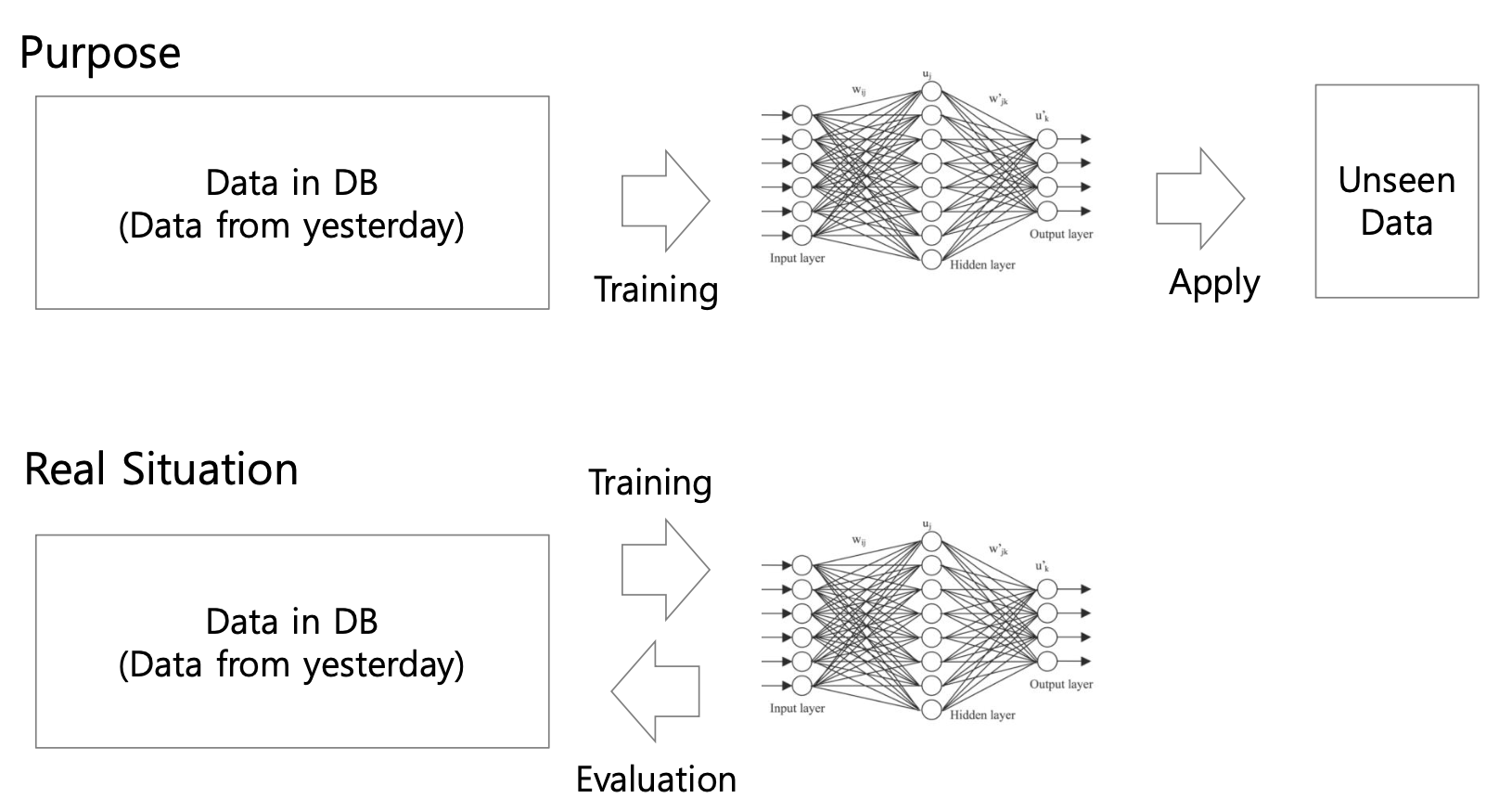

Training performance : 훈련 데이터에 대한 모델의 성능 측정
Test performance : 테스트 데이터에 대한 모델의 성능 측정. 보통 일반화 성능과 관련이 있다.

테스트를 위한 별도의 데이터셋을 마련하는 경우는 적다. 그럼에도 우리는 통계적 학습 이론(Statistical Learning Theory)에 기반하여 테스트 성능이 일반화 성능을 대변한다고 믿는다.

i.i.d assumption

i.i.d assumption이란, 훈련 데이터와 테스트 데이터가 동일한 확률 분포로부터 독립적으로 샘플링된다는 가정이다.

동일한 확률 분포에서 각 데이터가 독립적으로 샘플링될 경우, 훈련 데이터셋으로 학습한 모델이 테스트 데이터셋에서도 동일하게 작동할 것이다.

이 가정을 보장하기 위해 지켜야할 점은 다음과 같다.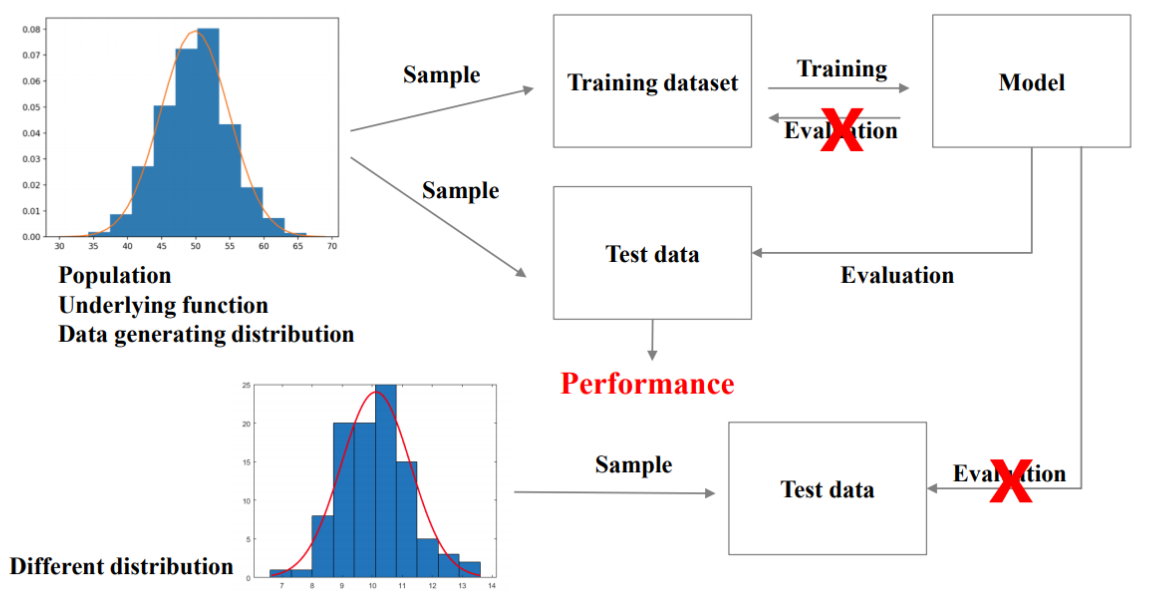

테스트 데이터로 훈련을 진행하면 안됨.
테스트 데이터와 훈련 데이터는 동일한 확률 분포에서 추출되어야 한다.
- 테스트 데이터가 훈련 데이터와 다른 확률 분포에서 추출되었다면, 테스트 성능은 일반화 성능을 대변할 수 없다.

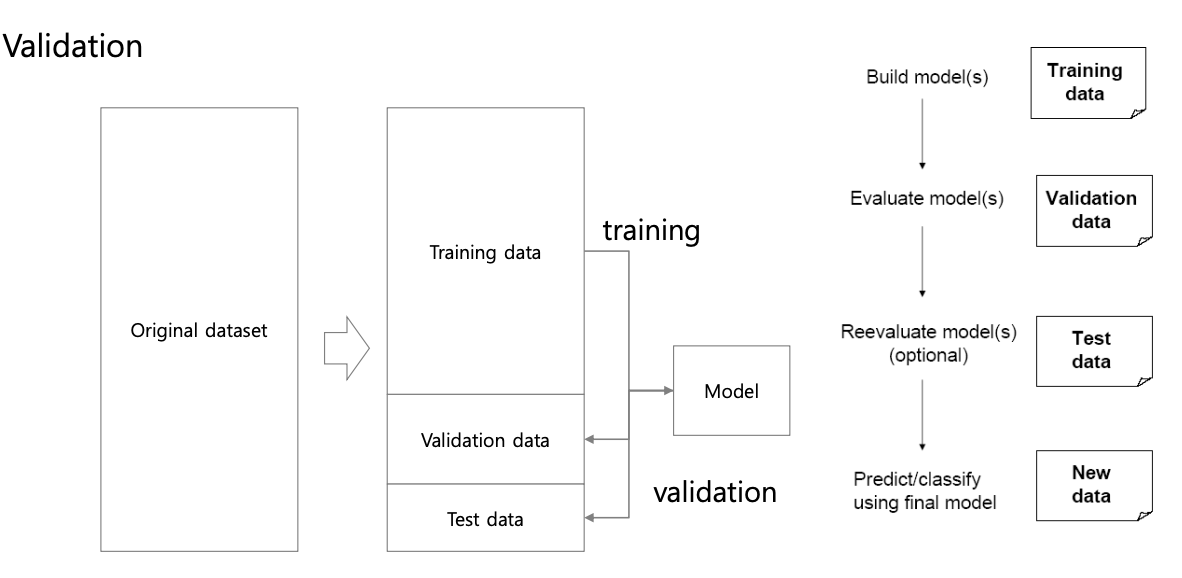
Validation Dataset

Training Dataset : 모델 학습을 위한 데이터셋
Validtaion Dataset : 학습 중간에 모델 성능을 평가하고 튜닝하기 위한 데이터셋
Test Dataset : 최종 모델을 평가하기 위한 데이터셋, 일반화 성능을 대변

K-fold cross validation

Validation Dataset을 생성할 때 K-fold corss validation을 자주 활용한다.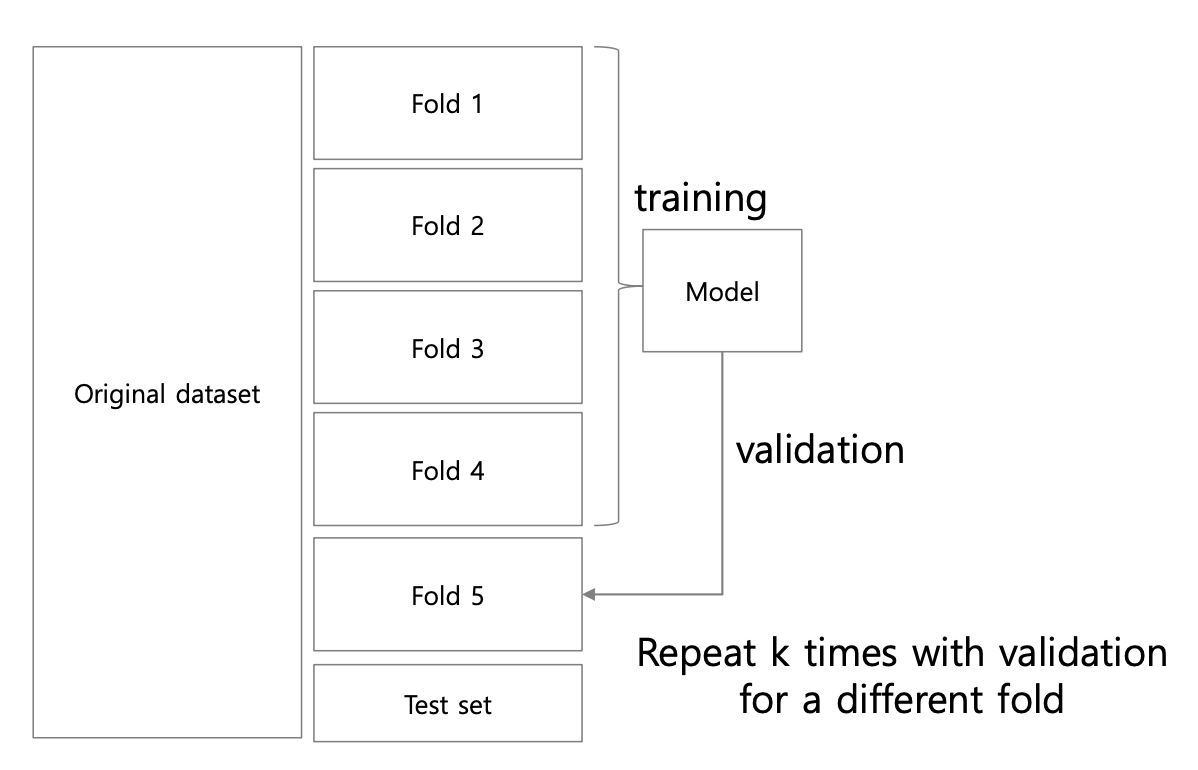

1) 전체 데이터(Batch)를 k등분 (k-fold)

2) $1$ fold for Validation

3) $k-1$ fold for Training

4) 총 $k$ 번 반복하여 전체 fold를 한번씩 validation dataset으로 사용

Model Capacity

Model Capacity(모델 용량)이란, 모델을 구성하는 파라미터의 수를 의미한다. Model Capacity가 크다는 것은 파라미터가 많은 복잡한 모델이라는 의미와 같다.

Model Capacity에 따라 모델이 근사할 수 있는 함수의 복잡도가 결정된다. 즉, 모델 용량이 커질수록 $가설공간^{*}$ 의 크기도 커진다.

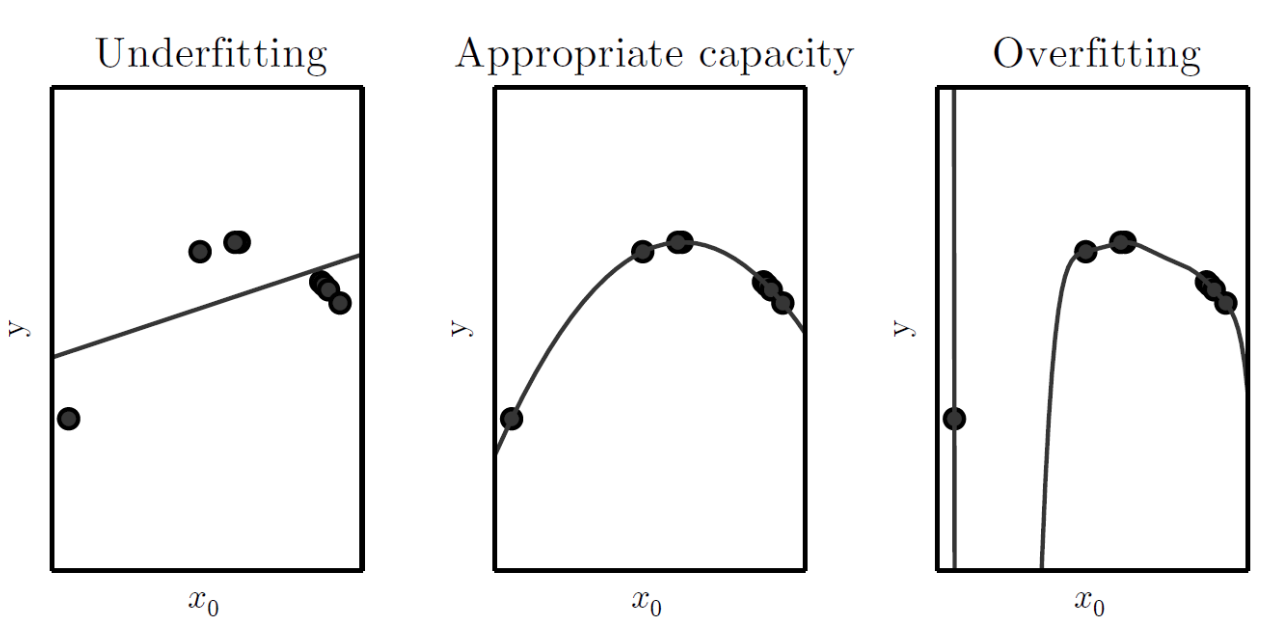
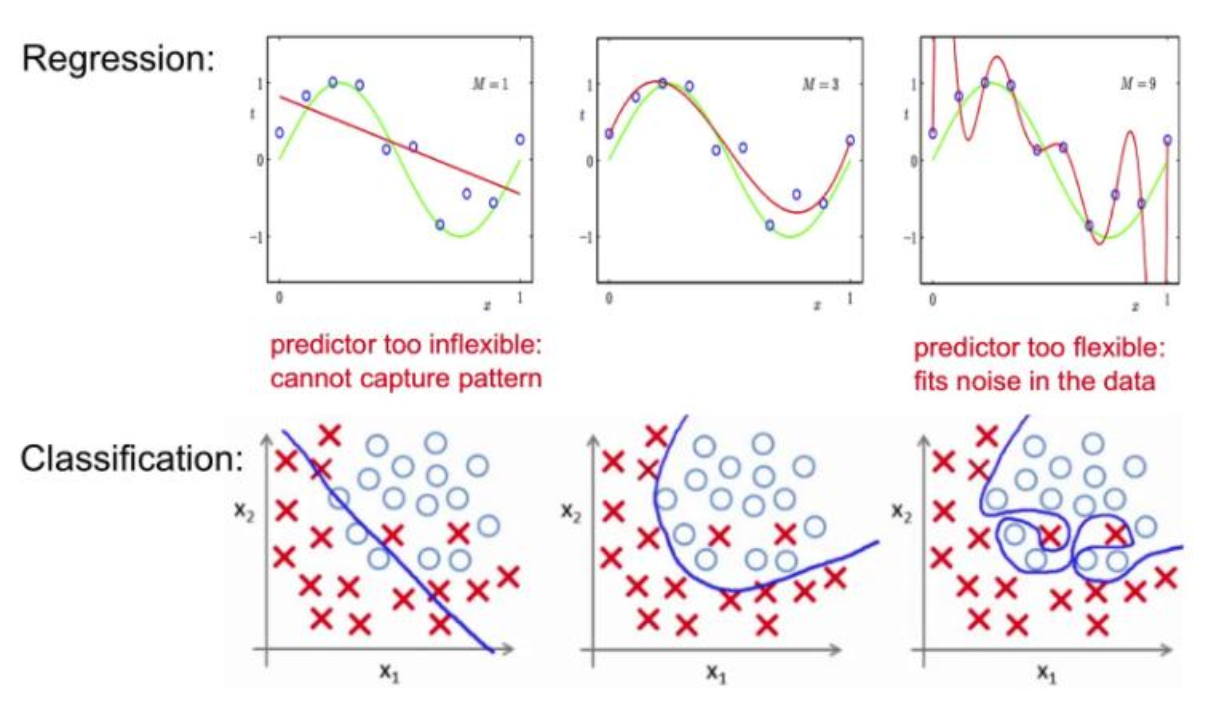
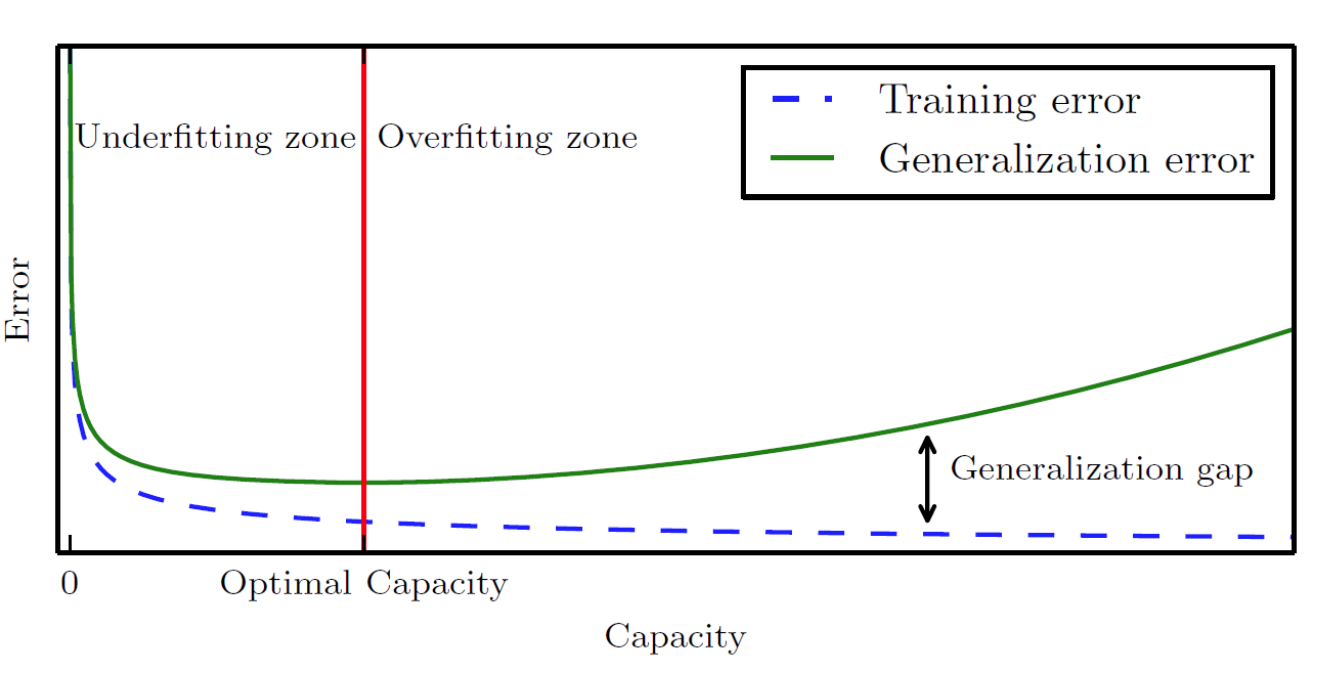
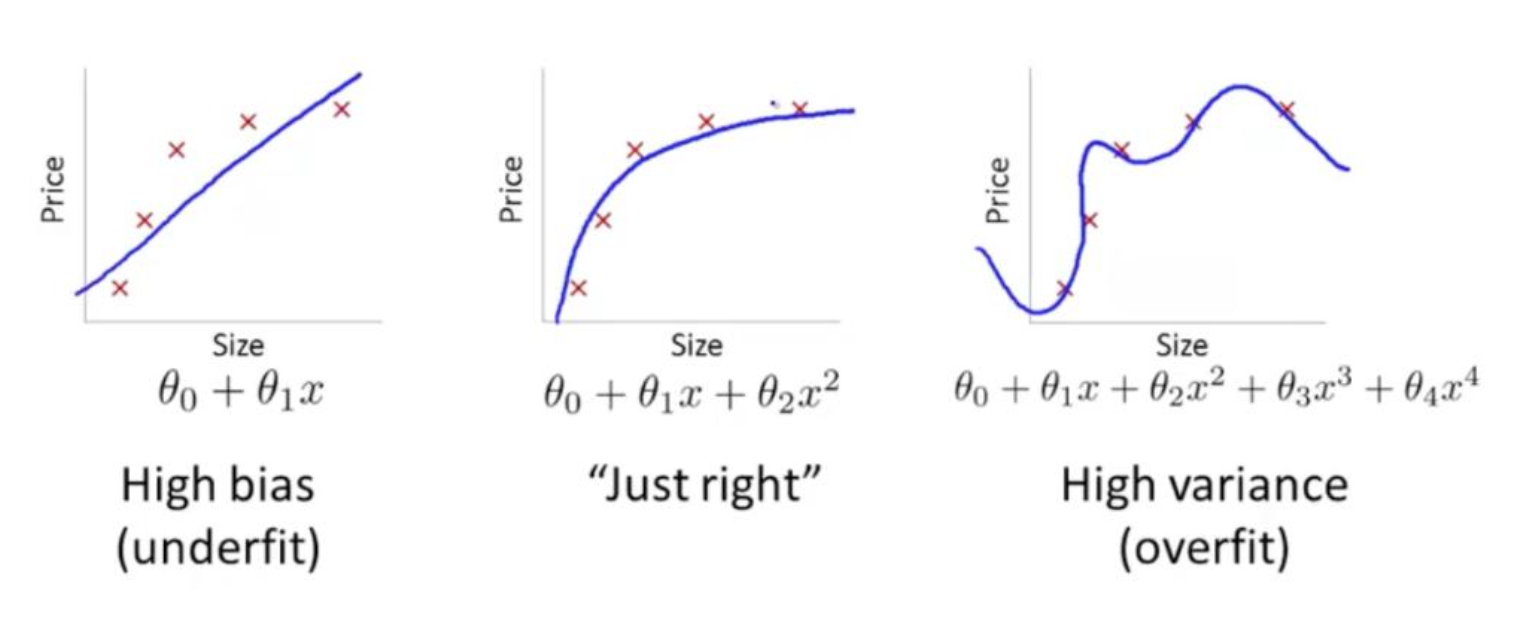
* Hypothesis Space(가설 공간) : 모델이 선택할 수 있는 함수들의 집합

복잡한 모델일수록 Model Capacity가 크며, 복잡한 모델일수록 과적합(Overfitting)의 위험성이 증가한다.

과적합은 모델이 지나치게 복잡할 때 발생
훈련 데이터에 대해서는 예측 성능이 뛰어나지만, 일반화 성능이 떨어짐
모델 용량을 낮추기 위해 정규화(Regularization) 기법이 활용됨

Model Capacity가 작은 모델은 지나치게 단순한 구조일 가능성이 높다. 이는 복잡한 연산이 불가능하다는 의미이며, 과소적합(Underfitting)의 위험성이 존재한다.

과소적합은 모델이 지나치게 단순할 경우 발생
어떤 데이터에 대해서도 예측 성능이 떨어짐
Model Capacity를 증가시키거나, 훈련 데이터셋의 크기를 증가시켜 과소적합을 회피

Parameter and Hyperparameter

Parameter(파라미터)는 학습이 진행됨에 따라 업데이트되는 값으로, 파라미터가 모델의 예측 성능을 결정짓는다.

Hyperparameter(하이퍼 파라미터)는 파라미터를 제어하기 위한 목적으로 사람이 설정하는 값이다. 따라서 고정된 값으로 유지되며 학습의 진행 속도를 조절한다.

Parameter vs Hyperparameter

파라미터

모델 내부에 존재 (weight, bias, etc...)

학습의 대상

하이퍼파라미터

모델 외부에서 인위적으로 설정 (learning rate, etc...)

파라미터의 튜닝이 목표 (학습 대상이 아님)

Estimation

Estimator(추정량)은 모델이 목표 값 $\theta$ 를 추정하기 위해 사용하는 수식이나 방법을 의미하며, 일반적으로 모델이 추정한 값은 $\hat{\theta}$ 로 표기한다.

정답 : $\theta$
추정값 : $\hat{\theta}$

Bias-variance trade-off

Bias(편향)이란, 추정값과 정답값의 차이를 의미한다.

bias(\hat{\theta}) = \mathbb{E}[\hat{\theta}] - \theta

Variance(분산)이란, 추정값의 분포가 흩어져있는 정도를 나타낸다.

var(\hat{\theta}) = \mathbb{E}[(\hat{\theta}-\mathbb{E}[\hat{\theta}])^2]

(Bias-variance trade-off) 일반적으로 Bias를 줄일 경우 Variance가 증가하고, Variance를 줄일 경우 Bias가 증가한다.

MSE를 최소화하기 위해 편향과 분산 사이의 균형을 찾아내 정의한 MSE 함수는 다음과 같다.

MSE = Variance + Bias^2

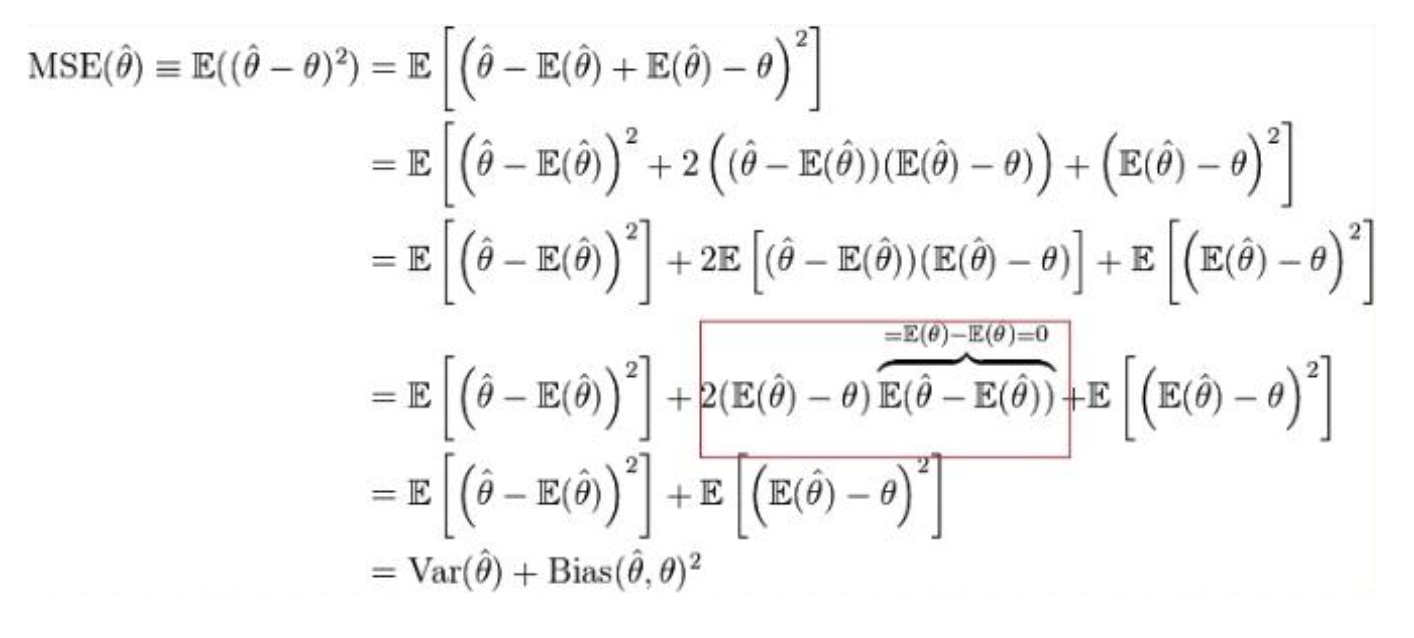
Maximum Likelihood Estimation

데이터를 추출한 모집단의 분포에 대한 정보가 없다고 생각해보자.

주어진 데이터들을 가장 잘 설명할 수 있는 분포(Likelihood)를 찾을 수 있다면, 해당 데이터의 모집단의 분포와 근접할 확률이 가장 높지 않을까?

위와 같은 생각에서 시작된 것이 바로 Maximum Likelihood Estimation(MLE, 최대 우도 추정)이며, 이는 파라미터를 추정하는 방법 중 가장 대표적인 방법 중 하나이다.

다음 예시를 살펴보자.

우리는 $m$ 개의 샘플을 갖고 있다.
$X = [x^{(1)}, x^{(2)}, ..., x^{(m)}]$
우리는 샘플이 어떤 분포에서 추출되었는지 모른다.
모델의 파라미터를 $\theta$ 라고 할 때, 우리는 데이터가 추출된 모집단과 가장 유사한 확률 분포를 찾고싶다.
최대 확률 분포가 모집단과 가장 유사한 확률 분포일 확률이 높다.
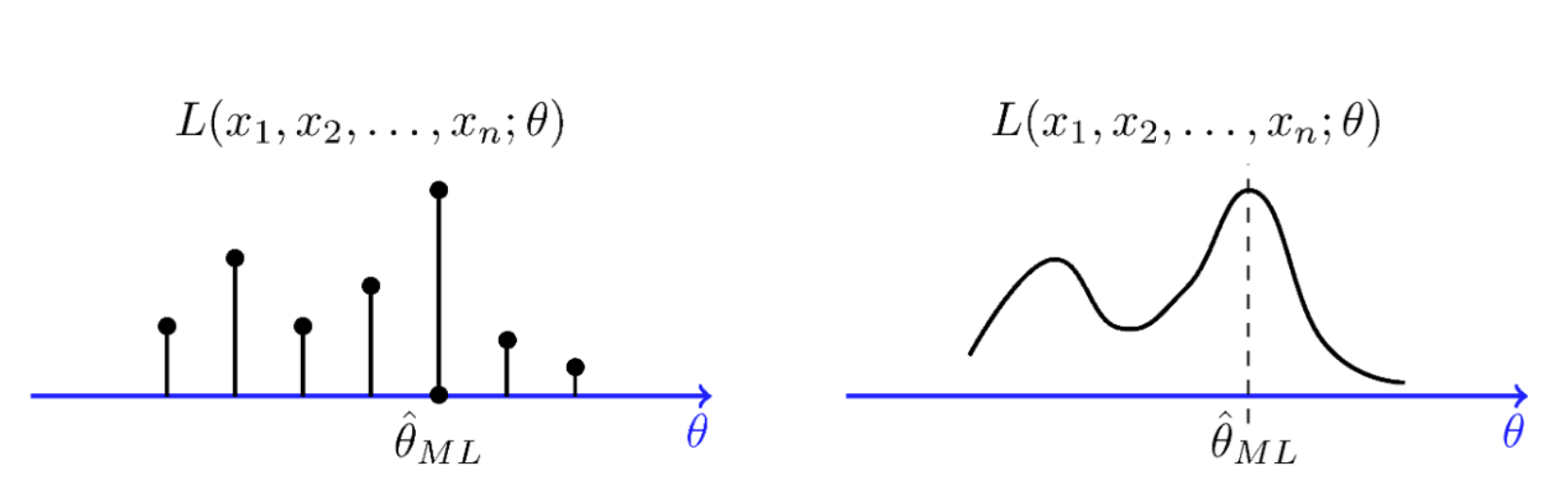
따라서 MLE는 다음과 같이 정의한다.

\theta_{ML} = \argmax \prod_{i=1}^{m} p_{\text{model}}(x^{(i)}; \theta)

연산의 안정성을 위해 log와 함께 사용하는 것이 일반적이다.

\theta_{ML} = \argmax \sum_{i=1}^{m} log{p_{\text{model}}(x^{(i)}; \theta)}

Bayesian Statistics

통계학을 관통하는 두 가지 시각이 존재한다.

Frequentist(빈도 주의)는 고정된 정답 $\theta$ 가 존재하며, Point estimation(점 추정)를 통해 정답을 추정할 수 있다고 본다.

Bayesian(베이즈 주의)는 정답 $\theta$ 는 불확실성을 갖고 있으며, 이에 대한 확률 분포를 추정해야 한다는 관점이다.

확률은 믿음의 정도를 반영할 뿐이다.
데이터 관측 이전 데이터에 대한 사전 지식을 확률로 표현 : $p(\theta)$
데이터 관측 이후(Posterior), Likelihood 획득 : $p(X|\theta)$
파라미터에 대한 확률 업데이트 : Bayes' rule
$P(\theta|X) = \frac{p(X|\theta)p(\theta)}{p(X)}$

MLE는 우리가 어떤 파라미터를 추정할 때, likelihood를 최대로 하는 확률 분포를 찾는 과정이다.

MLE는 우리가 알고 있는 데이터의 사전 지식 정보는 반영하지 않는다는 한계점이 존재한다.

우리가 데이터에 대해 갖고 있는 사전 정보를 활용하여 Posterior를 최대화 하는 파라미터를 찾는 추정법을 Maximum A Posterior(MAP)이라고 하며, 다음과 같이 정의한다.

\theta_{MAP} = \argmax p(\theta|X) = \argmax p(X|\theta)p(\theta)

MLE의 경우와 마찬가지로, 연산의 안정성을 위해 log를 활용하는 것이 일반적이다.

\theta_{MAP} = \argmax log p(\theta|X) = \argmax logp(X|\theta) + logp(\theta)

Optimization

우리는 목적 함수(최적화 대상)가 어떤 형태인지 정확한 모양을 알지 못한다. 따라서 Gradient-based Method와 같은 방식을 활용하여 근사적으로 최적화를 진행한다.

어떤 함수의 도함수(기울기)를 구하여 기울기를 감소시키는 방향으로 $x$ 값을 조정하며 최적화를 진행하는 알고리즘을 Gradient Descent(경사 하강법)이라고 한다.

초기 위치 : $x_0$
다음 위치 : $x_1 = x_0 - \eta f^\prime(x_0)$
위 과정을 반복하며 최적해 탐색

머신러닝은 대부분 다음과 같은 형태의 벡터를 입력으로 받는다.

X = [x_1, x_2, ... ,x_n]

함수 $f(x)$ 는 사실 다음과 같은 형태를 띈다고 볼 수 있다.

f(X) = f([x_1,x_2,...,x_n])

따라서 기계학습에서 사용되는 함수의 도함수는 Partial derivatives(편미분)을 통해 구하는 것이 일반적이다.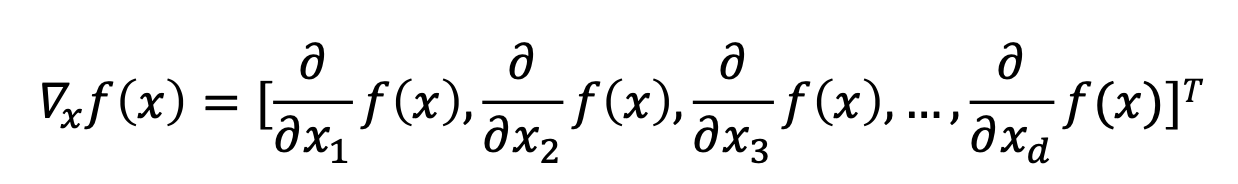

GD(Gradient Descent, 경사 하강법)은 모든 데이터를 사용해 기울기를 계산하기 때문에 계산 비용이 크다.

이를 해결하기 위해 일부 샘플 데이터(Minibatch)를 추출하여 기울기를 계산하는 Stochastic Gradient Descent(SGD) 기법을 활용하기도 한다.

Global Optimal(전역 최적점)은 이상적인 목표이지만, 현실적으로 찾기 어렵다. 또한 초기값을 잘못 설정하거나, 함수의 형태로 인해 Local Optimal(국소 최적점)에 갇히는 경우도 발생한다.

따라서 좋은 Local Optimal을 찾는 것이 현실적인 목표이며, 이를 Approximate Optimization(근사 최적화)라고 한다.

Information Theory

Information Theory(정보 이론)이란 불확실성을 수치적으로 표현하는 것으로, 어떤 사건이 발생하였을 때 해당 사건이 어느정도의 정보를 담고있는지 측정하는 것이다.

드물게 발생하는 사건이 흔히 발생하는 사건보다 더 많은 정보를 담고있을 가능성이 크다.

Entropy(엔트로피)는 확률 분포의 불확실성 정도를 수치로 표현한 것으로, 특정 랜덤 변수가 제공하는 정보량의 기댓값을 의미한다.

H(x) = -\sum_i{p(x_i)logp(x_i)}

Kullback-Leibler Divergence

두 확률 분포 사이의 차이를 측정하기 위해 Kullback-Leibler(KL) Divergence 라는 방식이 사용되는데, 다음을 살펴보자.

실제 데이터 분포 $P$
모델이 추정한 분포 $Q$

D_{KL}(P||Q) = \sum_ip(x_i)log\frac{p(x_i)}{Q(x_i)}

KL Divergence를 최소화 한다는 것은 모델이 추정한 분포가 실제 데이터의 분포와 유사해진다는 의미이다.

Cross-entropy

Entropy를 활용해서 정답과 예측 사이의 정보 손실을 계산할 수 있는데, 이를 Cross-Entropy라고 한다.

실제 데이터 분포 $P(x)$
모델이 추정한 분포 $Q(X)$

H(P,Q) = -\sum_i{P(x_i)logQ(x_i)} = H(P) + D_{KL}(P||Q)

$H(P)$ 는 실제 데이터 분포의 엔트로피
$H(Q)$ 는 모델이 추정한 데이터 분포의 엔트로피
$H(P,Q)$ 두 분포 사이의 Cross-Entropy

Cross-Entropy를 최소화 한다는 것은 정보 손실을 최소화 한다는 것이고, 이는 모델이 추정한 데이터의 분포와 실제 데이터의 분포가 유사하다는 의미이다.

이한량

한량 극복 프로젝트

다음 포스트