[Deep Learning] Chapter 3 - Neural Networks

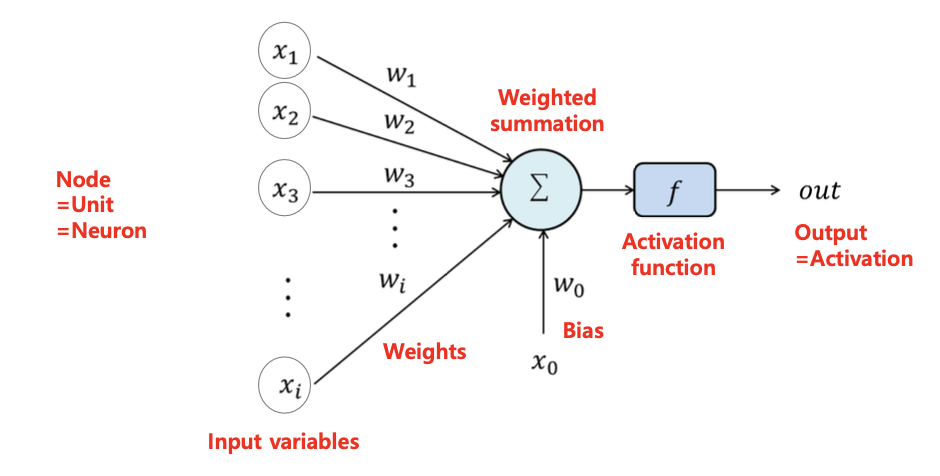
Neural Networks

Neural Networks란 인간 뇌의 뉴런 구조를 수학적으로 모방한 모델로, 여러 개의 간단한 연산 단위(노드 = 뉴런)의 연결로 복잡한 함수를 근사한다.

• 노드들은 서로 연결되어 있으며, 각 연결마다 가중치(Weight)가 존재한다.

• 출력층에 전달된 신호들은 합산되어 활성화 함수를 거쳐 최종 출력

가장 간단한 구조의 뉴럴 네트워크(Linear Machine)는 다음과 같다.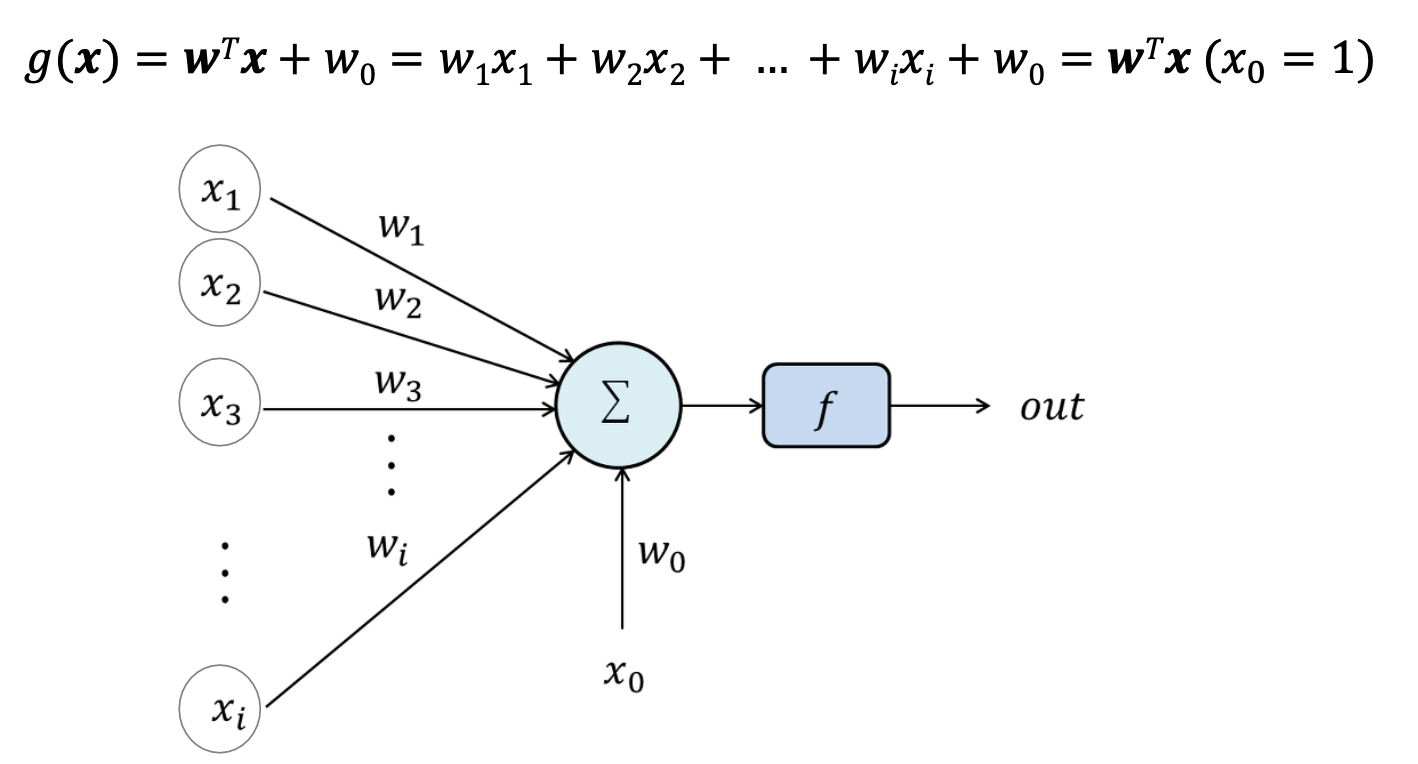

위와 같은 단순한 형태의 뉴럴 네트워크는 선형 분리 문제만 해결 가능하며, 비선형 문제(ex, XOR)는 해결하지 못하는 한계가 존재한다.

Optimization

최적화란, 모델의 성능을 개선하는 작업을 의미한다.

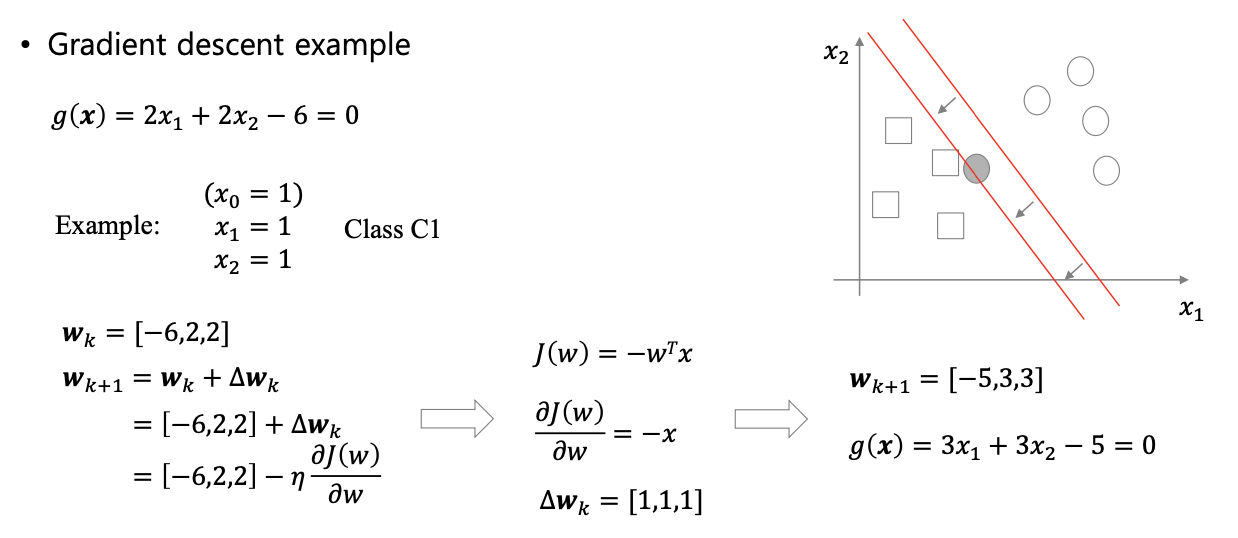
Gradient Descent(경사 하강법)은 손실 함수의 기울기가 감소하는 방향으로 값을 조정하며 최적화를 진행하는 기법이다.

최적화를 위해 손실 함수 기울기의 반대 방향으로 이동하면서 가중치 $w$를 반복적으로 업데이트한다.

오차는 정답과 예측값 사이의 차이로 정의하며, 오차가 클수록 해당 샘플에 대한 기울기가 커진다. 따라서 오차가 클수록 가중치의 업데이트 정도도 커진다.

• 손실 함수 $J(w)$를 최소화 하도록 가중치를 수정

• $w_{k+1} = w_k + \Delta w_k$

• $w_{k+1} = w_k - \eta \frac{\partial J(w)}{\partial w}$(편미분)

  • $\eta$는 하이퍼 파라미터로, 기울기의 증감 정도를 조정한다.

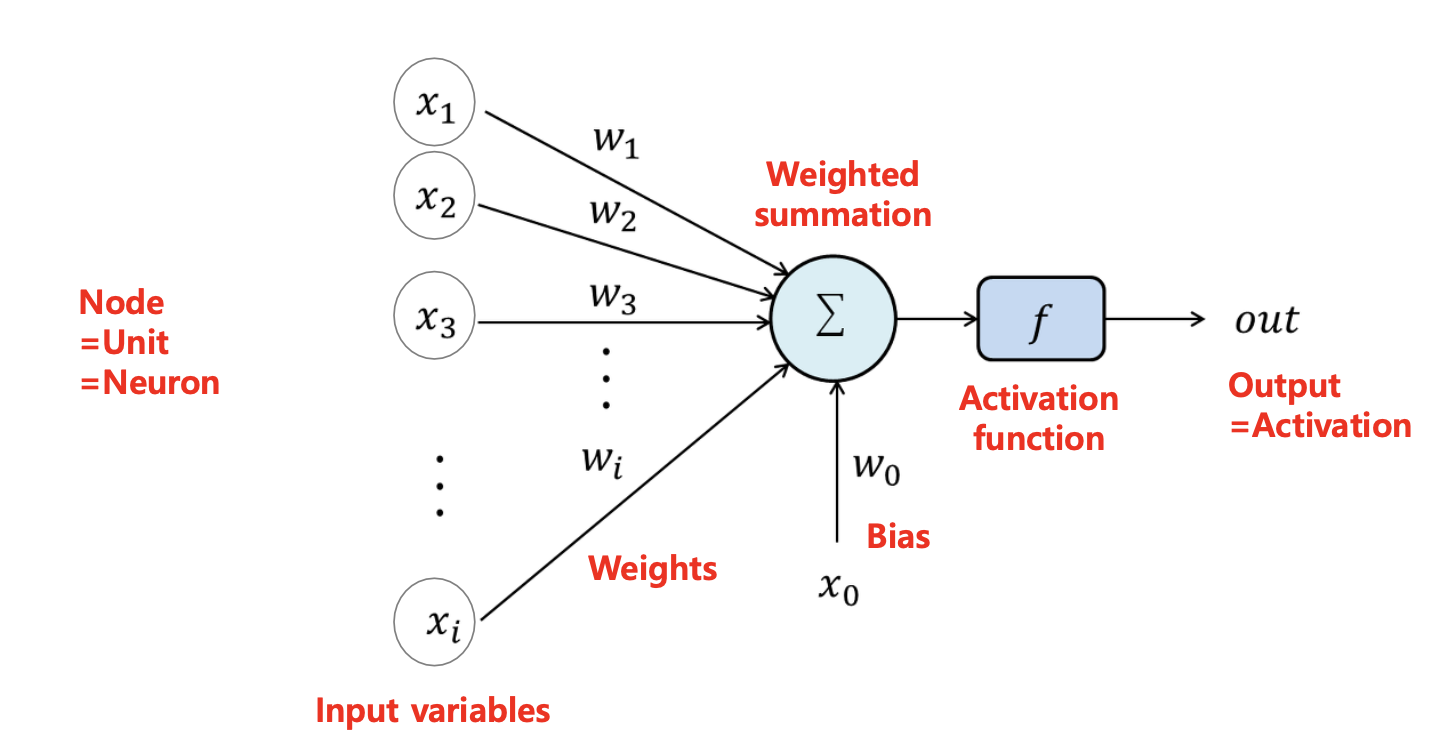
Perceptron

Perceptron은 입력층과 출력층이 직접 연결되어 있는 가장 단순한 형태의 인공 신경망이다.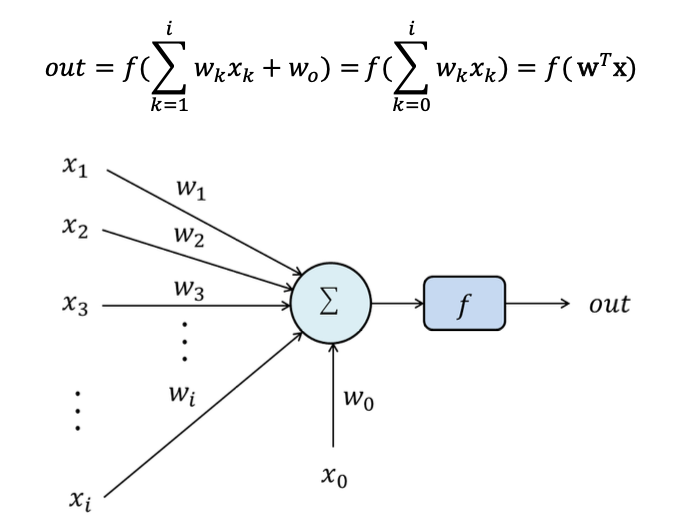

출력 노드는 출력값을 결정하기 위해 여러가지 종류의 함수를 사용하는데, 이를 Activation function(활성화 함수)이라고 한다.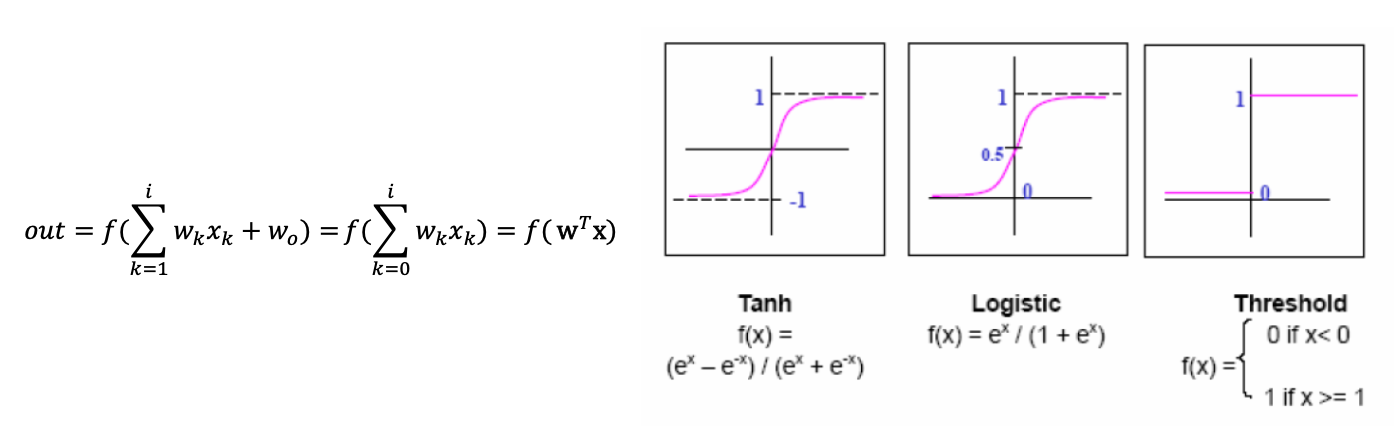

• Input : $z = w^Tx$

• Output : $f(w^Tx) = f(z)$

단일 퍼셉트론 모델은 비선형 문제(ex, XOR)를 해결할 수 없는 문제점이 존재한다.

이를 해결하기 위해 은닉층을 도입한 MultiLayer Perceptron(MLP)가 등장하였다.

은닉층은 입력층과 출력층 사이를 매개하며, 은닉층에 전달된 신호는 활성화 함수를 거쳐 출력층으로 전달된다.

은닉층은 활성화 함수를 통해 입력 신호를 새로운 공간에서 표현한다. 이러한 메커니즘으로 인해 비선형 변환이 가능해지는 것이다.

• 단순 퍼셉트론 : 입력층 - 출력층

• 다층 퍼셉트론 : 입력층 - 은닉층 - 출력층

은닉층과 적절한 가중치, 활성화 함수만 있다면 신경망은 어떤 연속적인 함수도 근사할 수 있는데, 이를 Universal Approximation Theorem (보편 근사 정리)라고 한다.

Feedforward Process

입력층에서 출력층으로 전달되는 방향의 신호를 순전파(Feedforward Process)라고 한다.

Input $\rarr$ Hid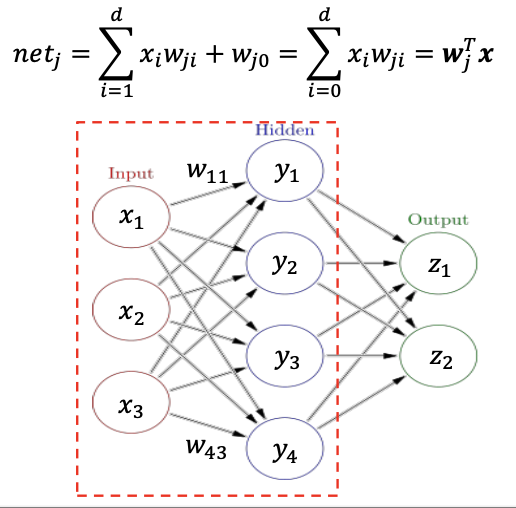deen

Hidden $\rarr$ Ou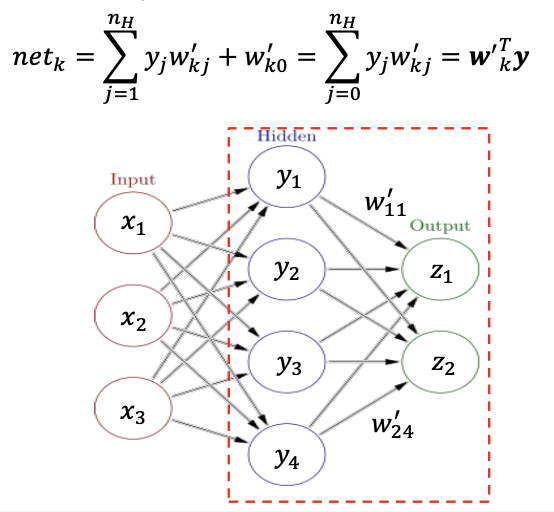tput

결론적으로, Input-to-Output 순전파는 다음과 같은 수식으로 나타낼 수 있다.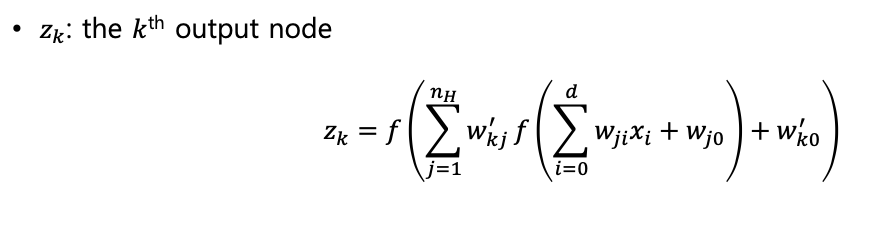

은닉층에서 출력층으로 신호를 전달할 때 왜 굳이 활성화 함수를 거쳐서 전달할까?

만약 은닉층에서 출력층으로 단순하게 신호를 전달한다면, 사실상 입력층과 출력층이 직접 연결되어 있는 구조와 동일하다.

비선형 활성화 함수가 없다면, 여러 층을 쌓더라도 전체 네트워크는 여전히 선형 변환의 조합이기 때문에 깊은 구조를 사용할 이유가 없다.

따라서 은닉층의 활성화 함수가 Non-linear transform을 진행한다고 이해할 수 있다.

Activation Function

출력층의 활성화 함수는 최종 출력을 결정한다. 주로 사용되는 활성화 함수를 살펴보자.

• 2-class classification (이진 분할) : Sigmoid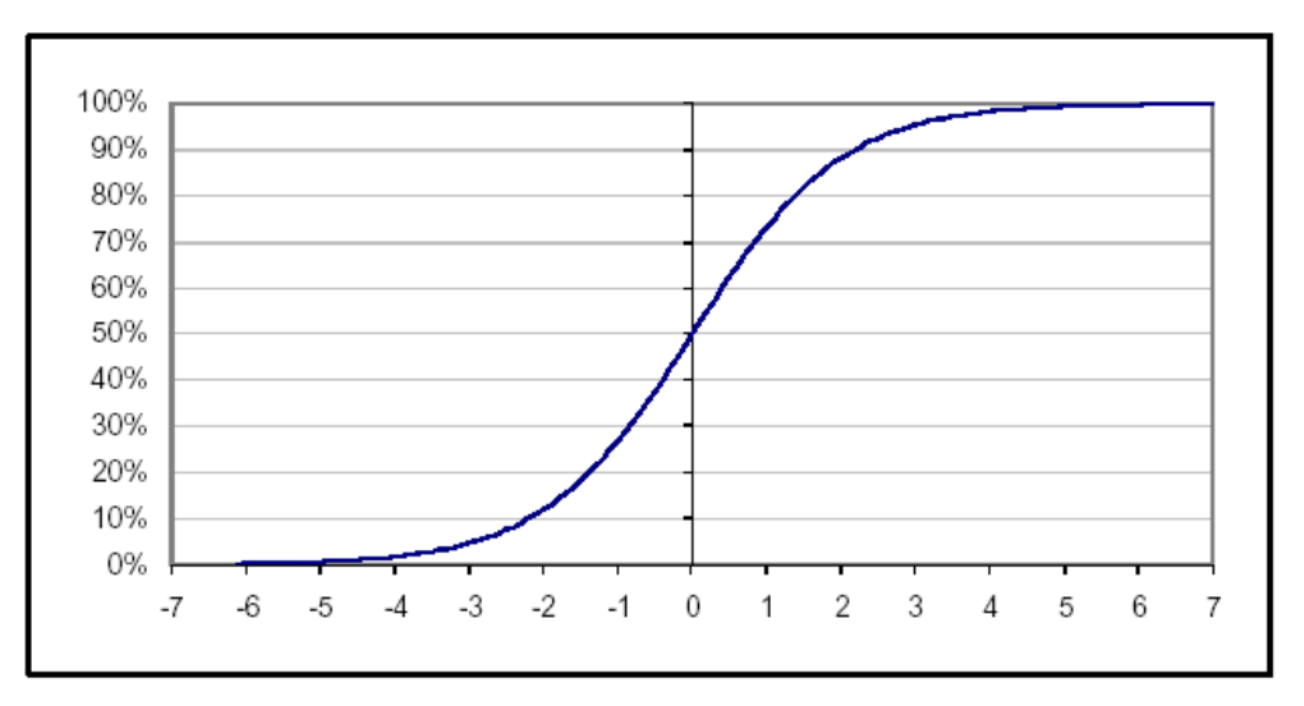

  $\delta(x) = \frac{1}{1+exp(-x)}, \hat{y} = \delta(w^Th + b)$

  • 출력은 0과 1사이에서 정의

  • 입력값이 커지면 1에, 작아지면 0에 수렴

  • 입력값이 0에서 멀어질수록 변화율이 매우 작아짐

• Multi-class classification (다중 분할) : Softmax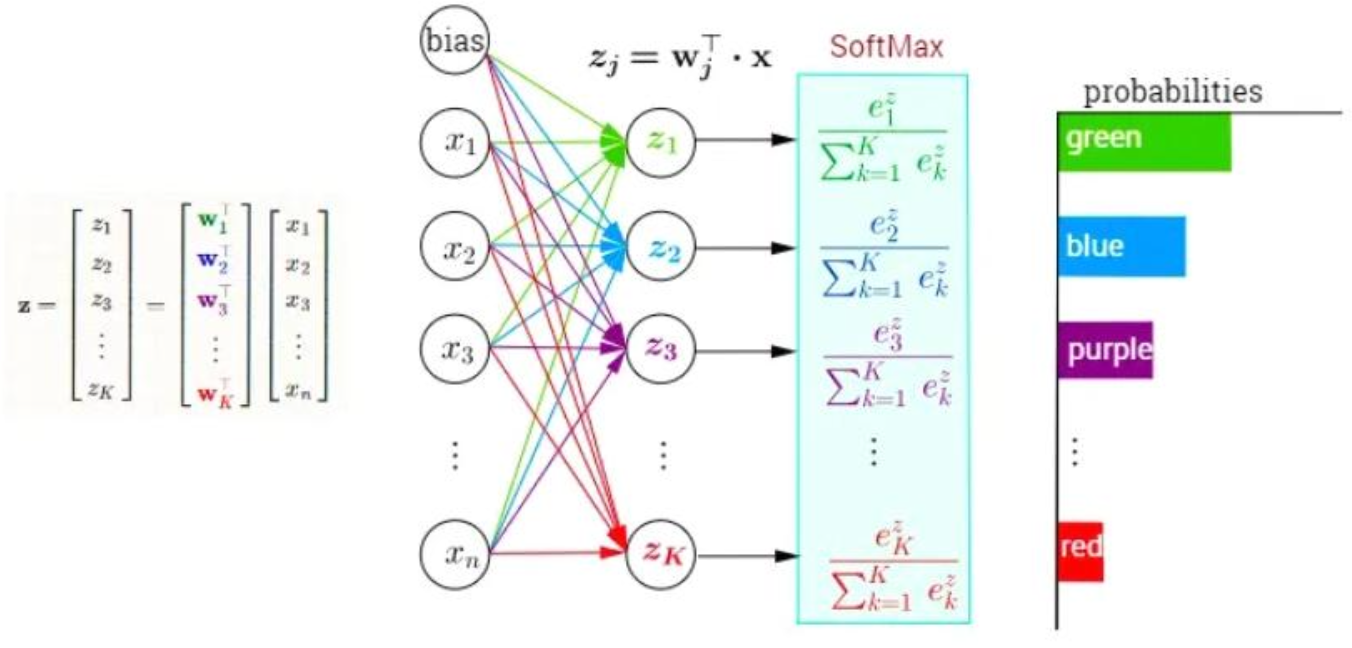

  $softmax(z)_i = \frac{exp(z_i)}{\sum_j exp(z_j)}$
  • Softmax : 각 샘플(데이터)이 각 클래스에 속할 확률 출력
    $\hat{y} = softmax(z_1) = 0.1 \\ \hat{y} = softmax(z_2) = 0.7 \\ ...$

• Regression (회귀) : Linear Units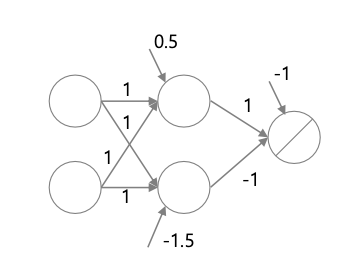

  $\hat{y} = W^Th + b$
  • 회귀 문제는 연속적인 수치를 예측하는 문제이기 때문에, 위와 같은 선형 함수를 주로 활용

Loss Function

Task에 따라 주로 사용되는 Loss Function에 대해서도 알아보자.

• Classification : Cross-entropy

  $J(w) = H(P, Q) = -\sum_i P(x_i)logQ(x_i) = -\sum_i z_ilog\hat{z_i}$

  • $z_i$ : 실제 정답

  • $\hat{z_i}$ : 모델이 예측한 확률

  • 엔트로피가 최소화된다는 것은, 정답을 예측할 확률이 높아진다는 것

• Regression : Mean Squared Error (MSE)

  $J(w) = \frac{1}{2}\sum_{k=1}^{n_O}(z_k - \hat{z_k})^2 = \frac{1}{2}||z - \hat{z}||^2$

  • $z_k$ : 실제 값

  • $\hat{z_k}$ : 예측 값

  • MSE가 감소한다는 것은, 정답과 예측 간 차이가 줄어든다는 것

Backpropagation

순전파와 반대로 출력층 방향에서 입력층 방향으로 전달되는 신호를 역전파(Backpropagation)이라고 한다.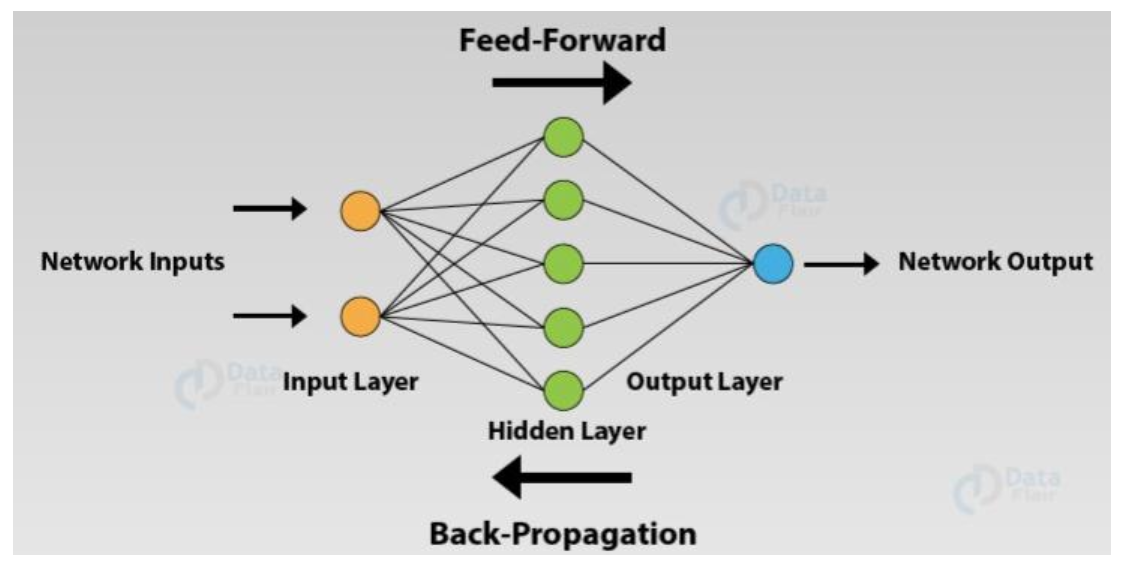

오차 역전파 알고리즘은 파라미터 업데이트를 위해 현재 가장 일반적으로 사용되는 핵심 기법이다. 이는 출력층에서 계산한 손실 함수의 기울기를 입력층 방향으로 전달하며 가중치(Weight)를 업데이트하는 방식이다.

직관적으로는 역전파 신호와 경사 하강법을 합친 방법으로 이해할 수 있다.

• 오차($E$)를 입력층 방향으로 전달하며 가중치를 업데이트

  • $E = y - \hat{y}$

  • $W \larr W - \eta \frac{\partial J}{\partial W}$