[Deep Learning] Convolutional Neural Networks

이한량·2025년 6월 2일

Deep Learning

목록 보기

5/10

Convolutional Neural Networks

Convolutional Neural Netwokrs(CNN, 합성곱 신경망)이란 그리드 구조(1D - 시계열 데이터, 2D - 이미지) 데이터의 국소적인 패턴을 감지하는 데 특화된 신경망이다.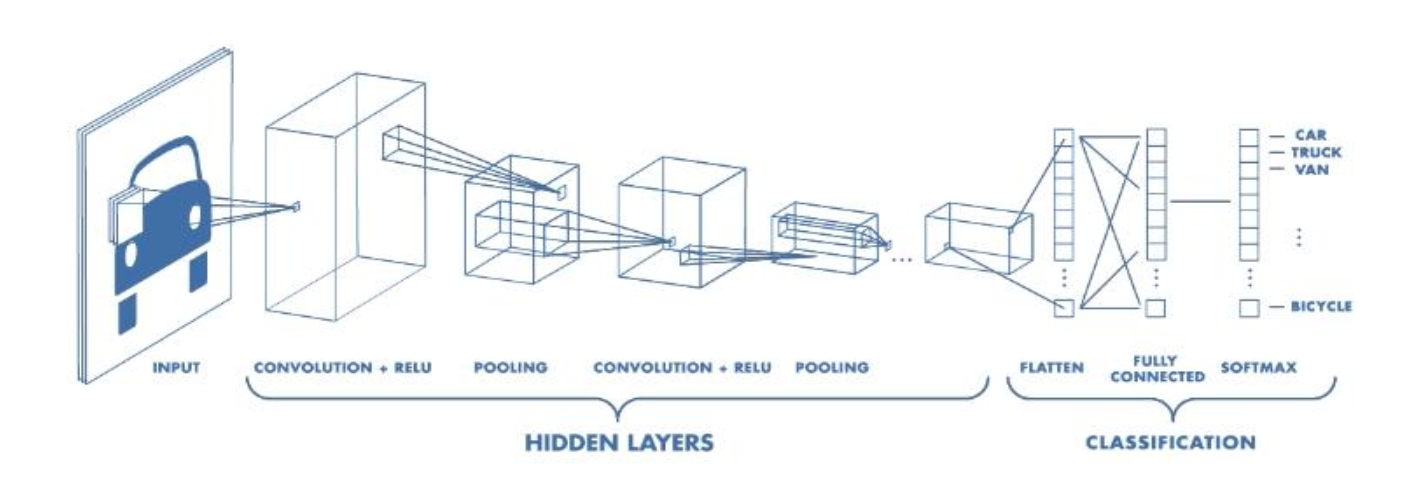

모든 CNN은 적어도 하나 이상의 합성곱 계층을 포함하고 있으며, CNN이 갖는 핵심적인 특징은 다음과 같다.

희소 연결(Sparse connections) : 고정된 크기의 필터에 의해서 합성곱 연산이 진행된다. 이로 인해 연산 효율성이 높으며, 지역적 특징을 더 잘 학습할 수 있다.
파라미터 공유(Parameter sharing) : 동일한 필터를 이미지 전체에 대해 적용하므로, 학습해야 할 파라미터의 수(=Filter size)가 매우 적다.
공간적 데이터(Spatial Data) : CNN은 특히 이미지 처리에 강점을 갖고 있다.

Convolutional operation

합성곱 연산은 다음과 같이 정의된다.

연속인 경우
이산적인 경우

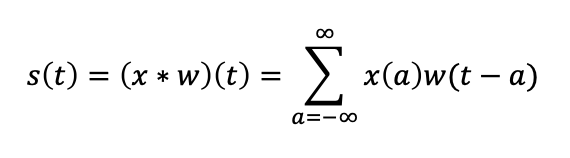
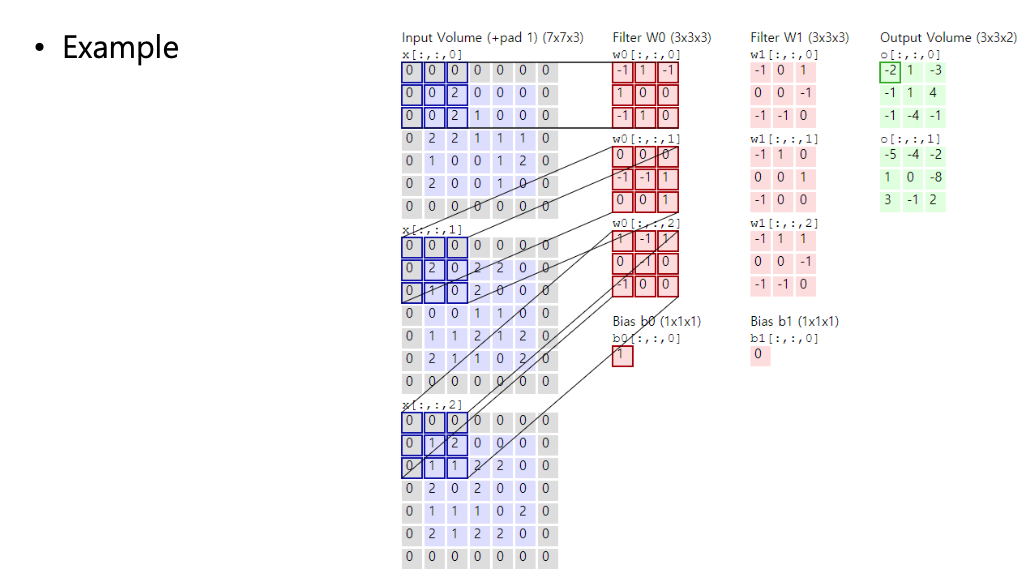
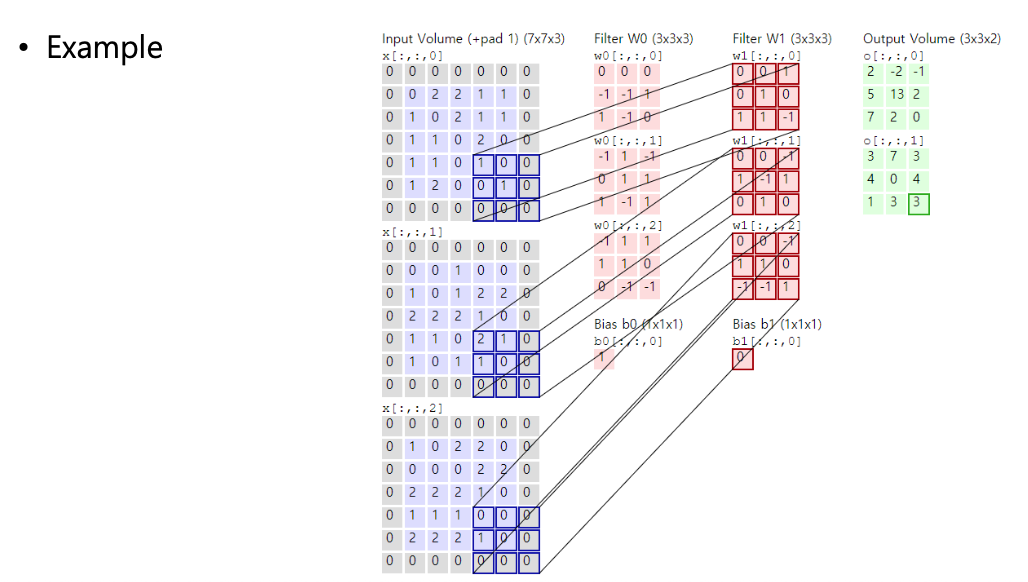
실제로 합성곱 연산이 어떻게 이루어지는지 예시를 살펴보자.

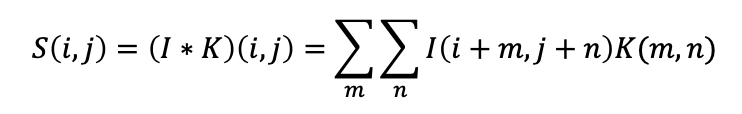
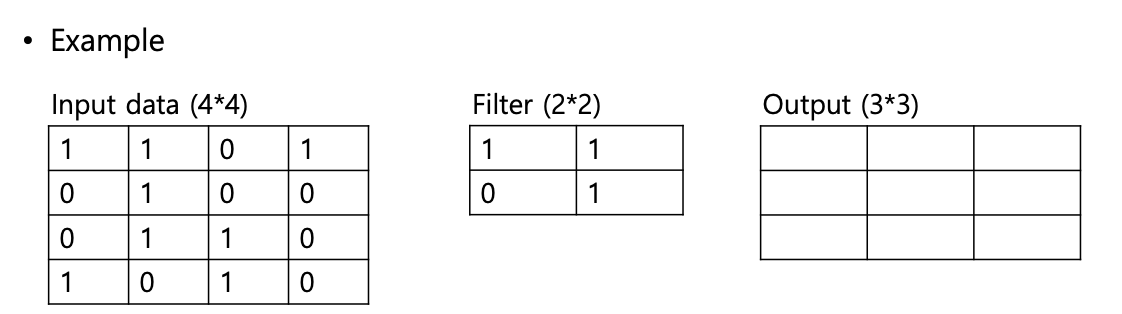
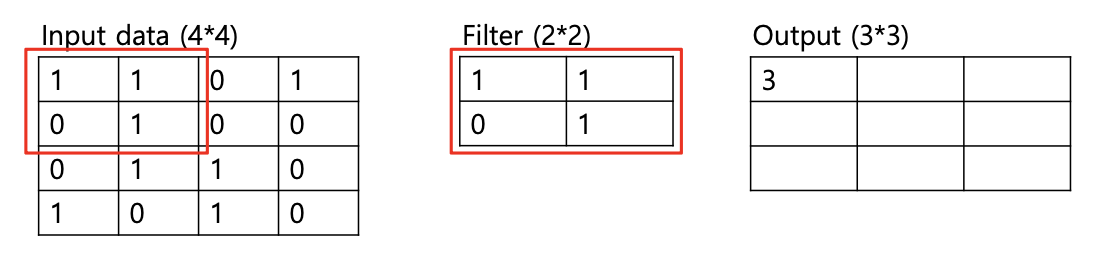
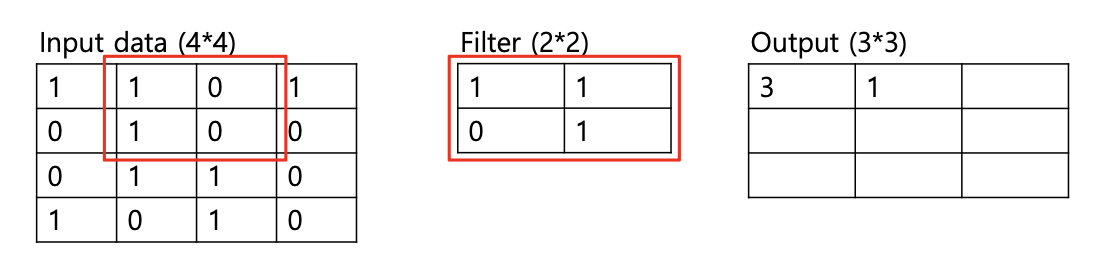
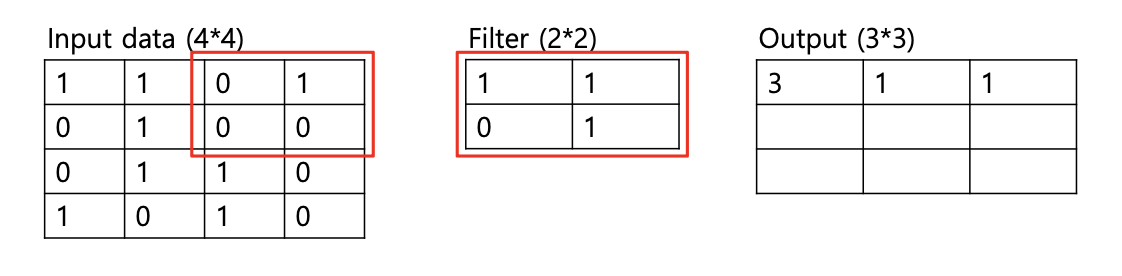
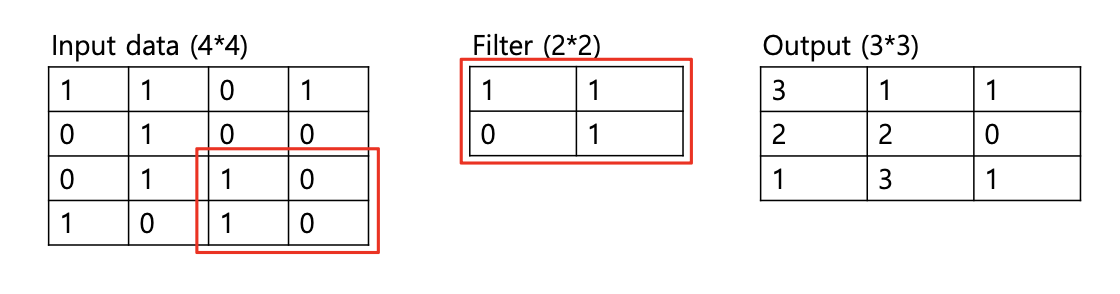
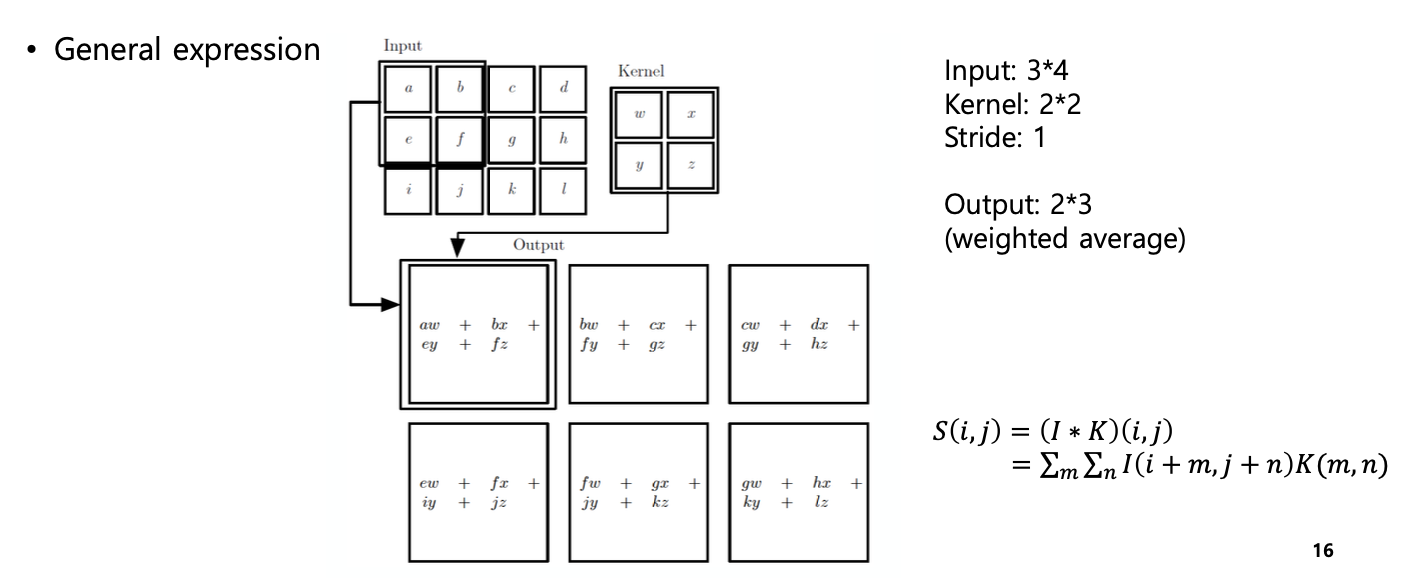
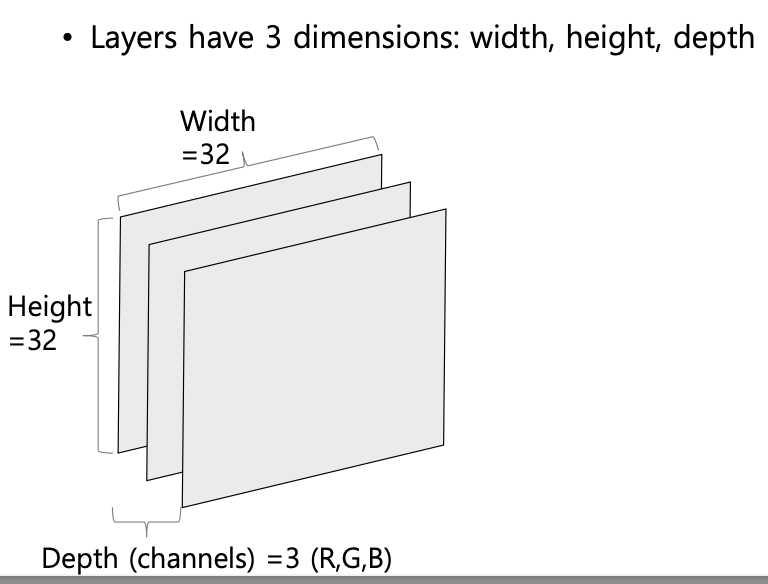
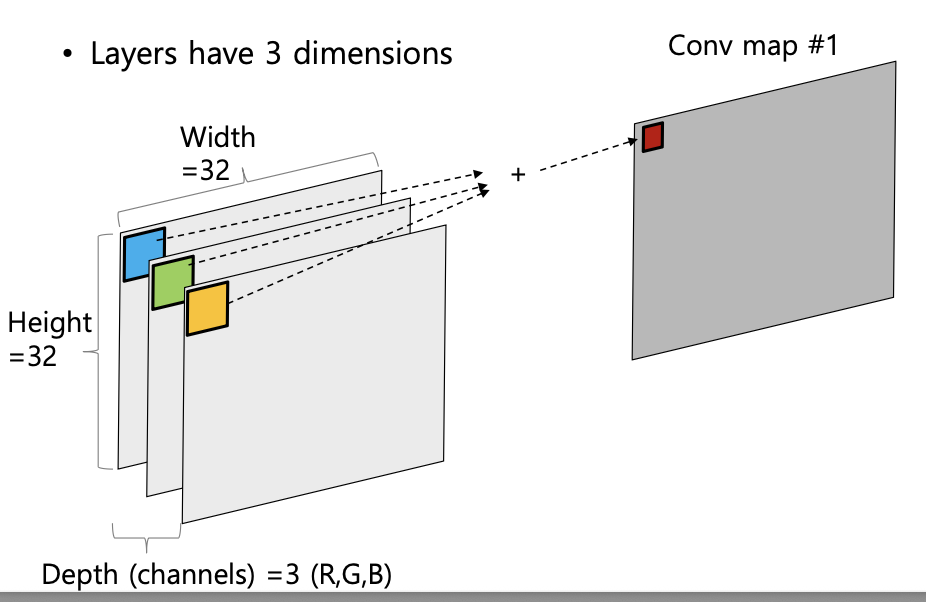
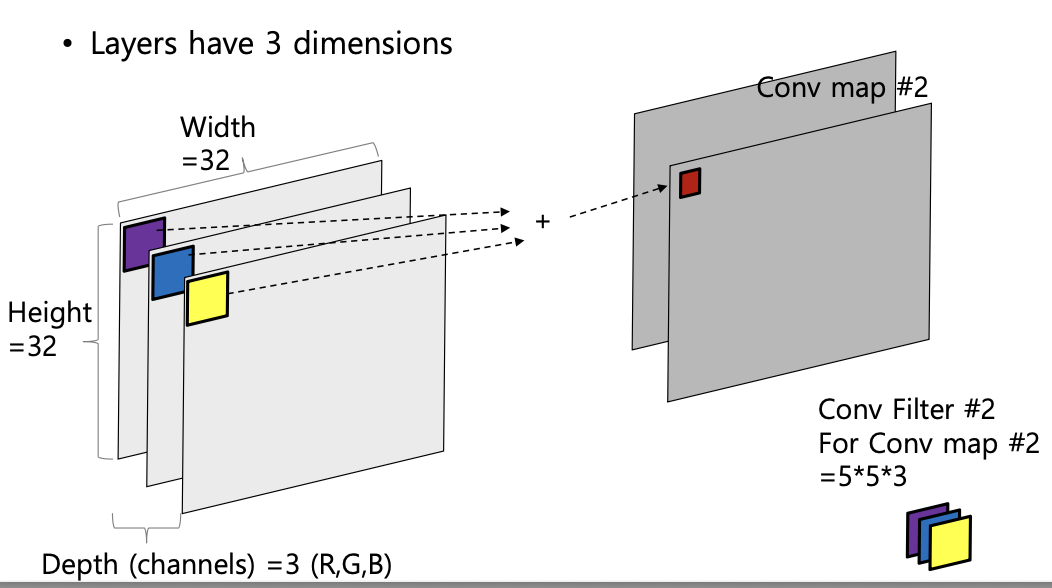
다중 채널(Ex, RGB 이미지)의 경우, 합성곱 연산은 다음과 같이 진행된다.

1) 각 채널별로 별도의 필터를 적용 (3가지)

2) 각 필터를 적용한 결과를 모두 합산하여 1개의 Convolution map 생성

3) 만약 필터의 개수가 $n$ 개라면, Convolution map의 depth $= n$

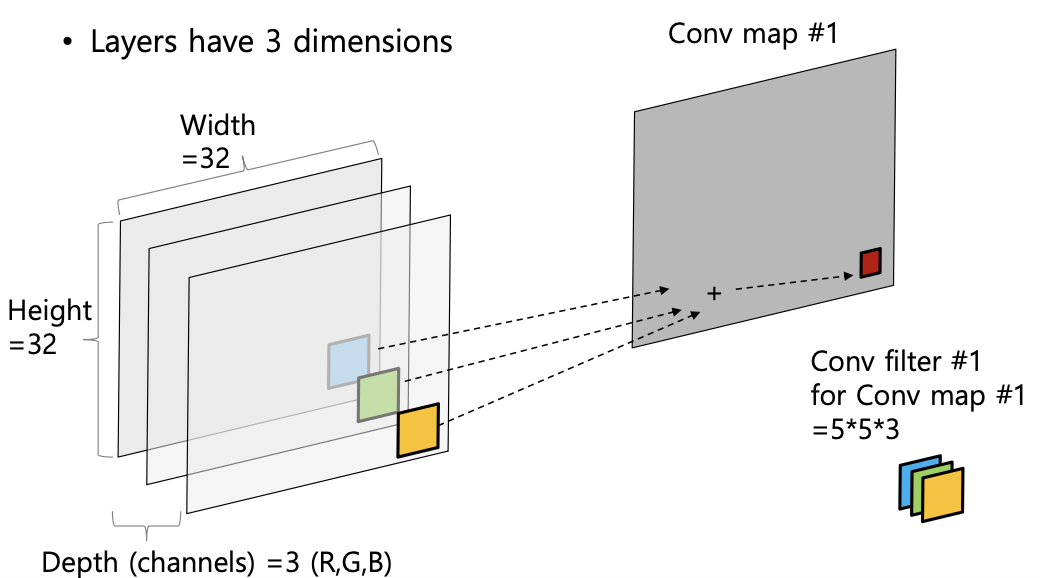
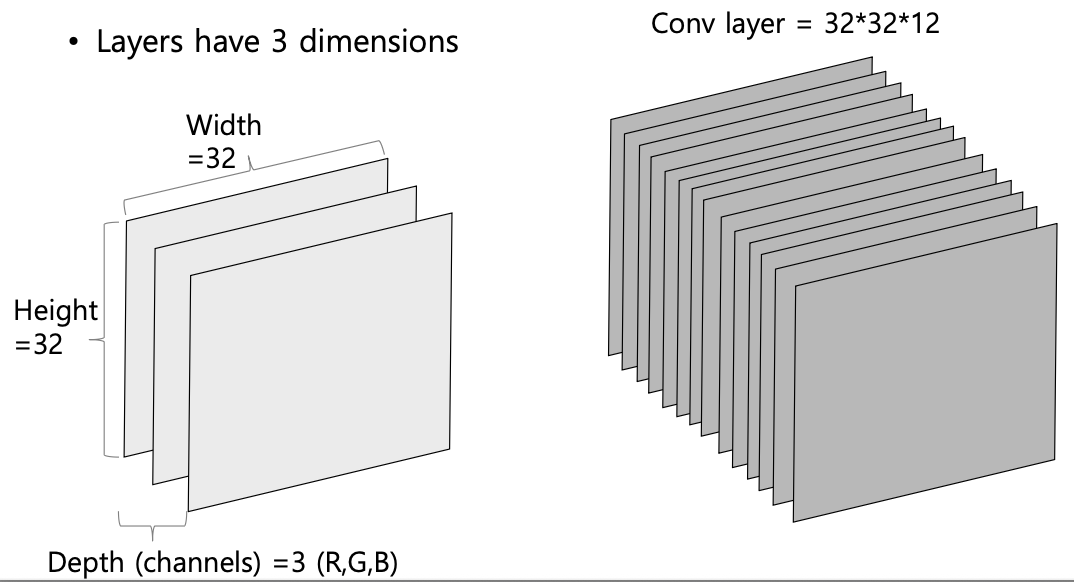
합성곱 연산으로 인해 CNN은 다음과 같은 특징을 갖게 된다.

희소 상호작용(Sparse interactions)

CNN의 합성곱 계층에서는 커널(필터)을 활용하여 데이터의 일부(Local)에만 합성곱 연산을 수행하며, 필터가 적용되는 영역을 수용 영역(Receptive field)이라고 한다. 이는 모든 입력에 대해 연결되는 MLP(Dense Connection)과 대비된다.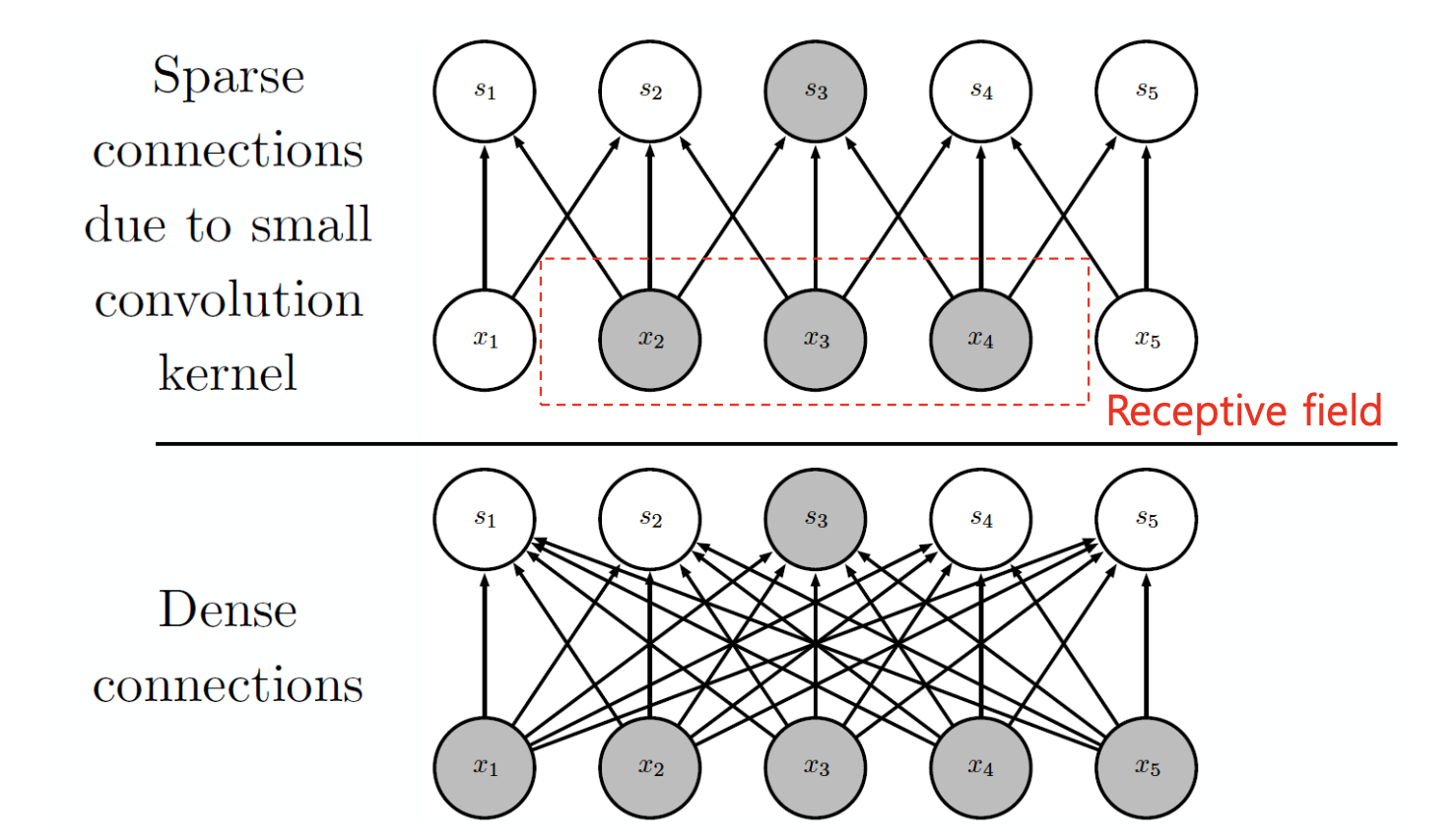

조밀 연결(Dense connection)은 모든 입력과 출력이 연결되어 있기 때문에 계산량이 크고, 입력의 지역적 특징(Local features)을 추출하기 어렵다.

반면 희소 연결(Sparse connection)의 경우, 일부 지역에 대해서만 합성곱 연산이 진행되므로 연산량이 적고 이미지의 지역 특징을 잘 추출할 수 있다.

CNN은 필터가 씌워진 부분과 뉴런이 직접으로 연결되며, 직접 연결이 형성된 특징의 영향력은 커지며, 간접 연결이 형성된 특징의 영향력은 작아진다.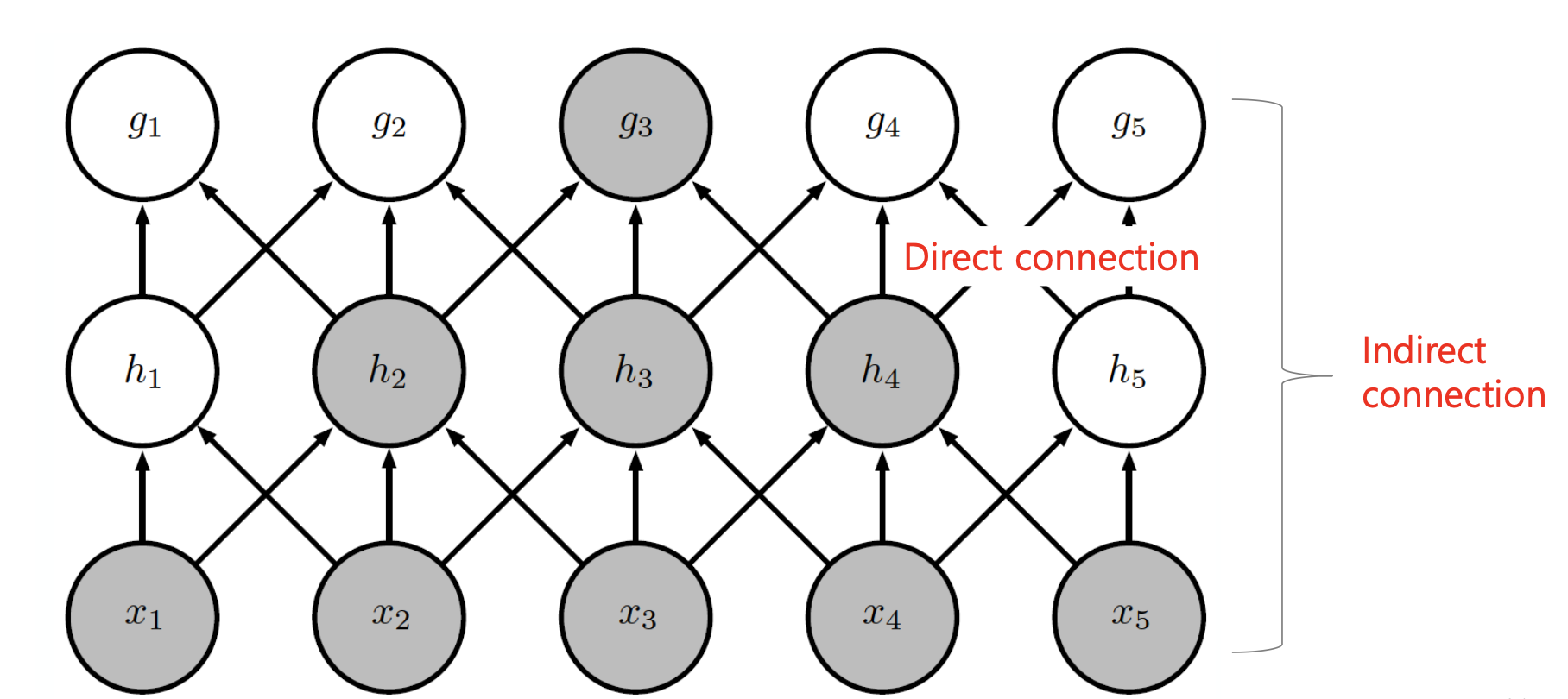

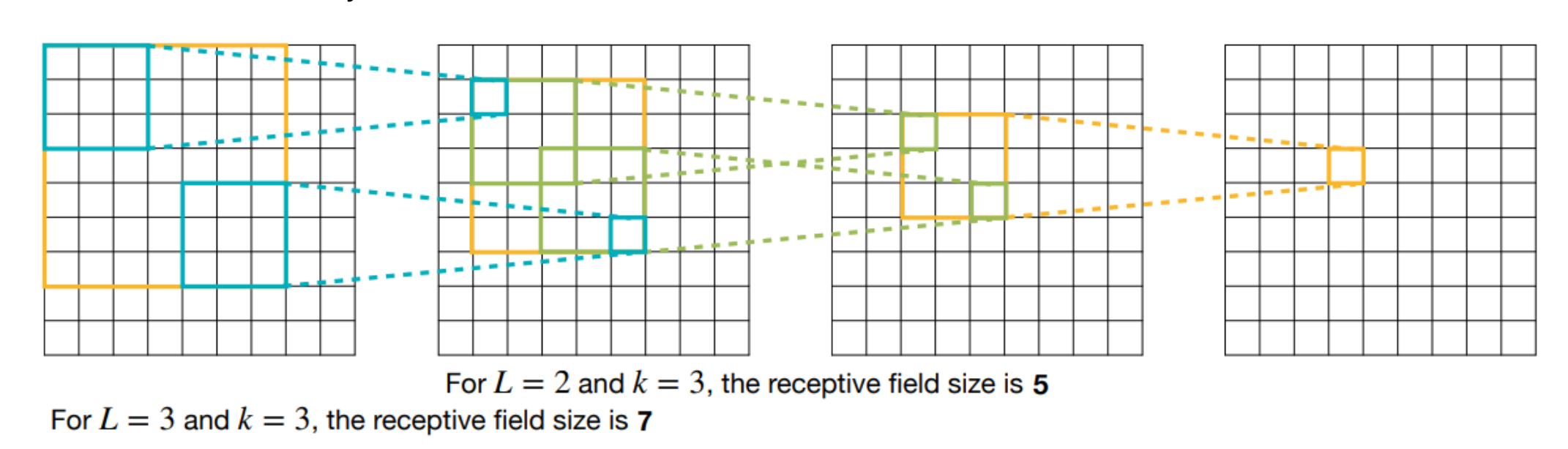
학습에 필요한 파라미터 수가 적고, 연산량이 적기 때문에 메모리와 계산 효율성이 좋다.

전통적인 신경망의 경우, 모든 입력 뉴런은 다음 계층의 모든 뉴런과 연결되며, 각 연결마다 고유한 가중치를 갖는다. 따라서 학습을 위해 사용되는 파라미터의 수가 매우 많은 구조이다.

반면 CNN의 경우, 동일한 필터를 이미지의 모든 위치에서 공유한다. 따라서 각 위치별로 고유한 파라미터가 불필요 하므로, 계산해야 할 파라미터 수가 매우 적다.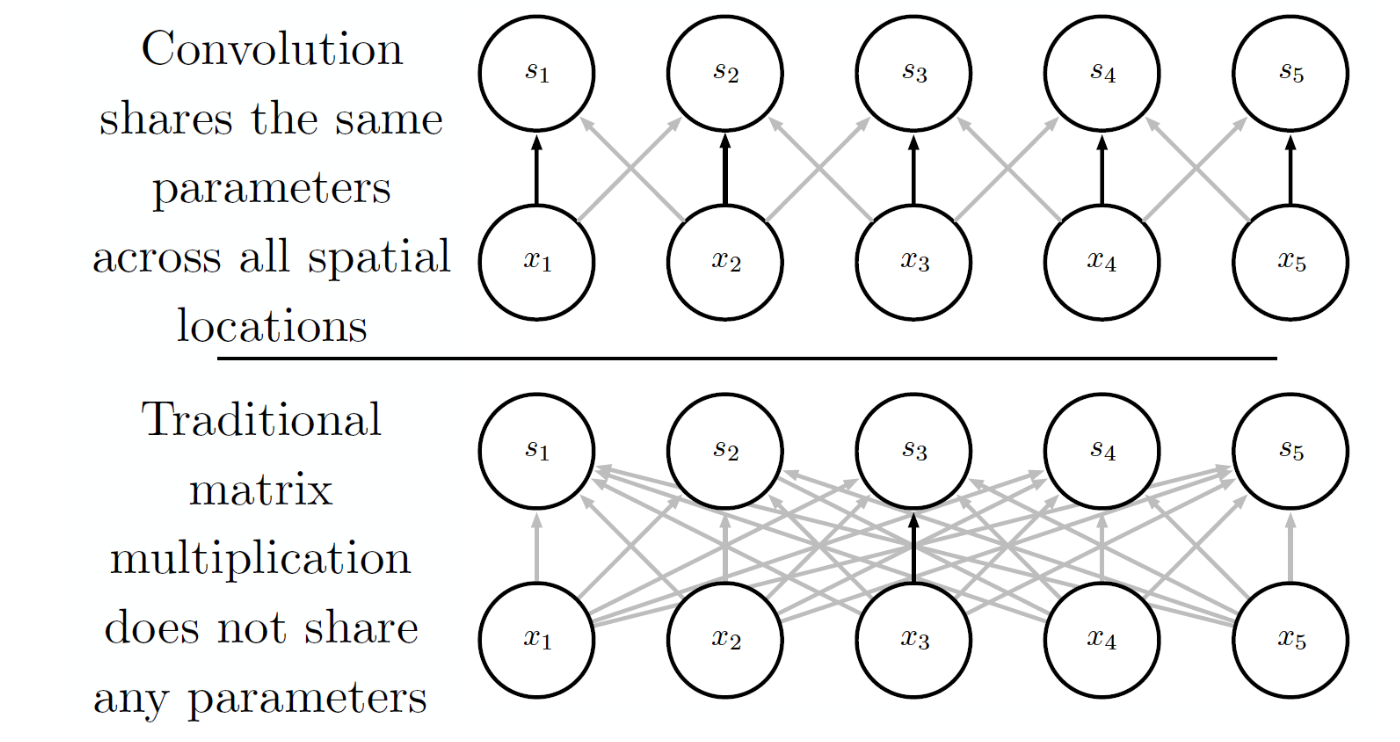

CNN의 이러한 특징은 계산해야 할 파라미터의 수를 줄이고, 이로 인해 높은 메모리 효율성을 갖게 된다. 또한 동일한 필터를 반복적으로 사용하는 것은 일종의 정규화(Regularization) 역할도 수행하게 된다.

등변 표현 (Equivariant representation)

등변성이란, 입력 데이터가 변함에 따라 출력이 동일한 방식으로 변형되는 성질을 의미한다.

f(g(x)) = g(f(x))

예를 들어 입력 이미지를 오른쪽으로 1픽셀 이동시키면, 출력 특징 맵도 똑같이 오른쪽으로 1픽셀 이동한다.

CNN에서 입력에 평행 이동 $g$ 를 적용한 후 합성곱을 수행한 것과 입력에 합성곱을 수행한 후 출력에 동일한 평행 이동 $g$ 를 적용한 것의 결과는 같다.

I(x,y) \rarr g(I) \rarr conv(g(I)) = I(x,y) \rarr conv(I) \rarr g(conv(I))

이러한 등변성은 입력이 변형되더라도 출력이 예측 가능하다는 것을 의미하며, 이는 로컬 패턴 감지와 변형에 대한 강건성을 갖도록 한다.

Pooling

Pooling은 특징 맵에서 특정 위치의 출력값을 주변 출력들의 요약 통계(Summary statistics)로 대체하는 방식이다.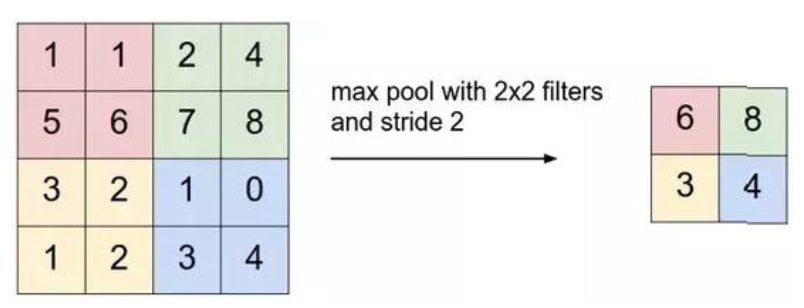

Max pooling : 가장 일반적으로 활용하는 방식; 영역 내 존재하는 값 중 최대값을 대표값으로 사용
Average pooling : 영역 내 존재하는 값들의 평균을 계산하여 대표값으로 사용

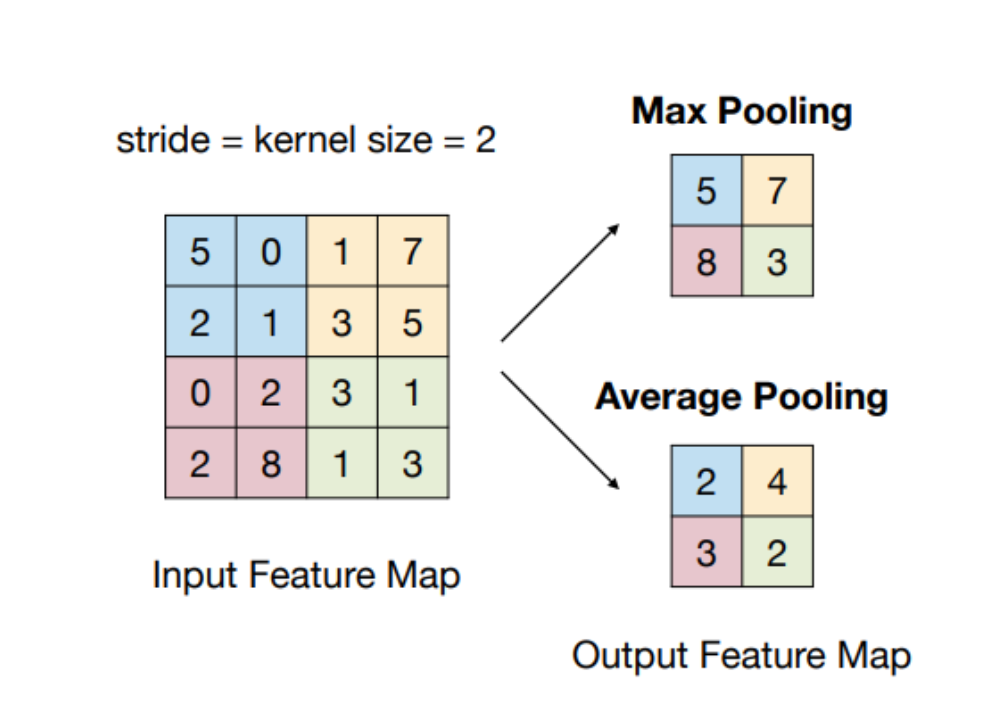
풀링은 이미지의 픽셀들을 요약하는 역할을 수행하므로, 이미지의 노이즈를 제거하고 강건성을 증가시키는 효과가 있다.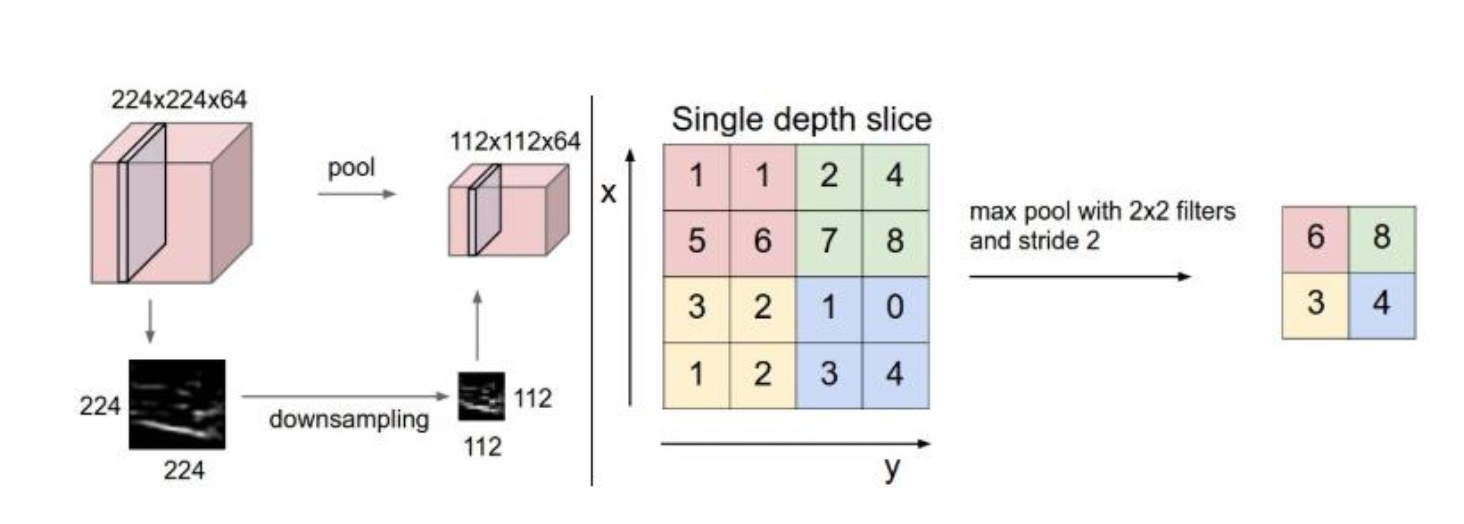

또한 풀링 연산은 $k$ 개의 유닛을 $1$ 개로 요약하기 때문에, 풀링 연산은 연산량을 줄여 계산 효율성을 높이는 데 도움을 준다.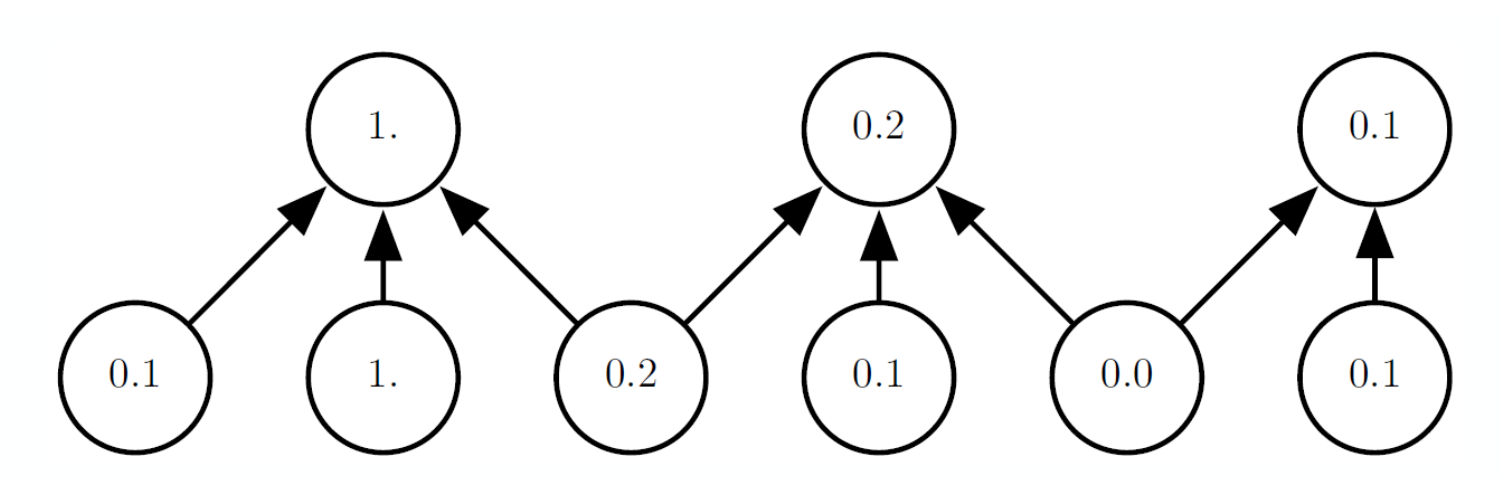

Variants of the basic convolution function

Stride

Stride란, 입력 데이터를 일정한 간격(2픽셀, 3픽셀)로 건너뛰며 합성곱을 수행하는 방식으로, 커널의 보폭을 설정하는 것으로 이해할 수 있다.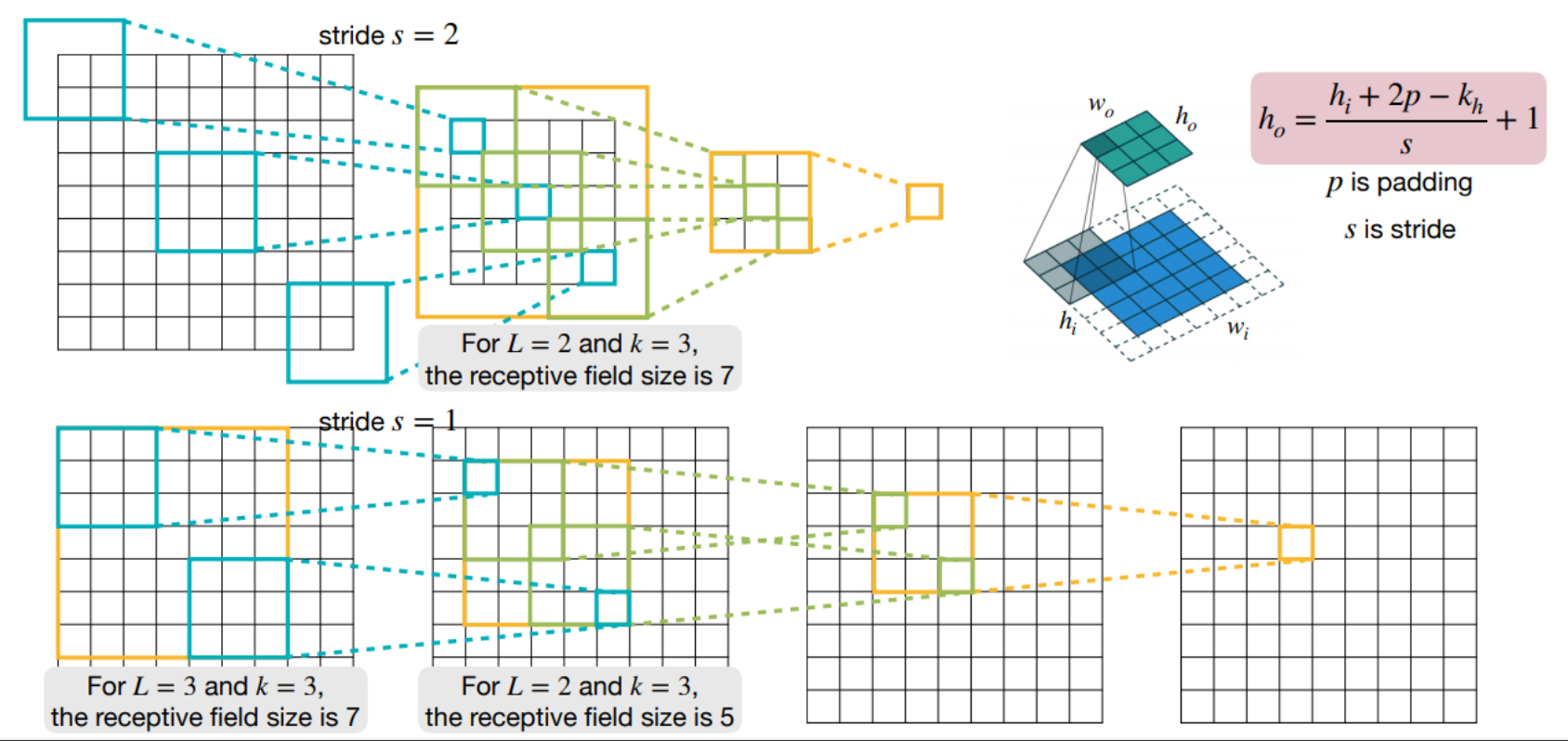

padding

합성곱 연산을 진행할 경우, 출력 이미지의 크기가 감소하는 단점이 존재한다. 이를 방지하기 위해 이미지에 패딩 픽셀을 추가하여 출력 이미지의 크기를 그대로 유지할 수 있다.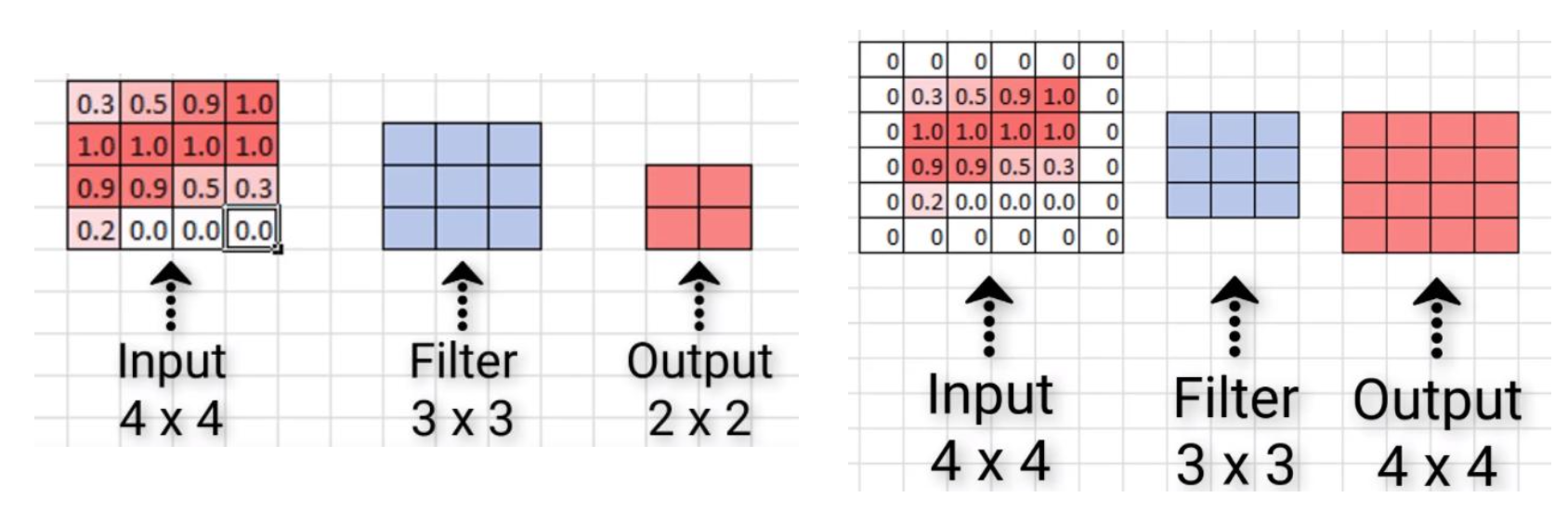

Zero-padding이 가장 일반적으로 사용되며, 이는 입력의 경계에 0으로 채워진 여백(Padding)을 추가하는 기법이다. 그 외에도 여러가지 종류의 패딩이 존재한다.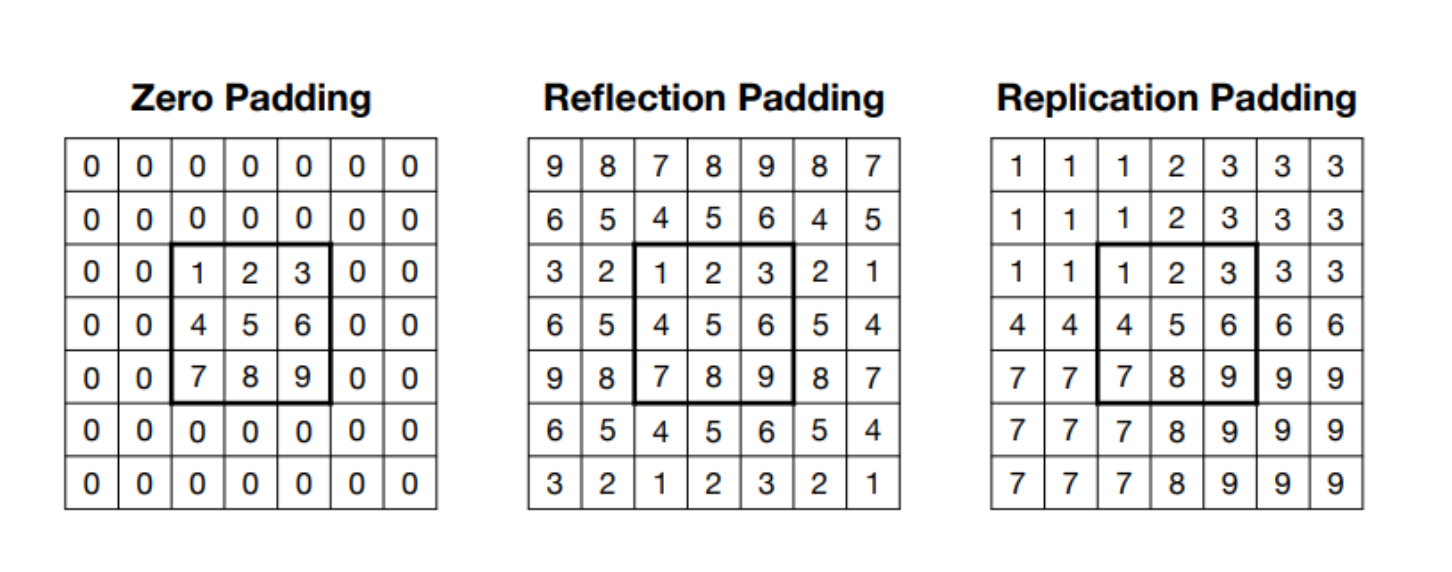

Unshared convolution

합성곱과 비슷하게 지역적인 연결을 가지지만, 파라미터를 공유하지 않는 방식이다.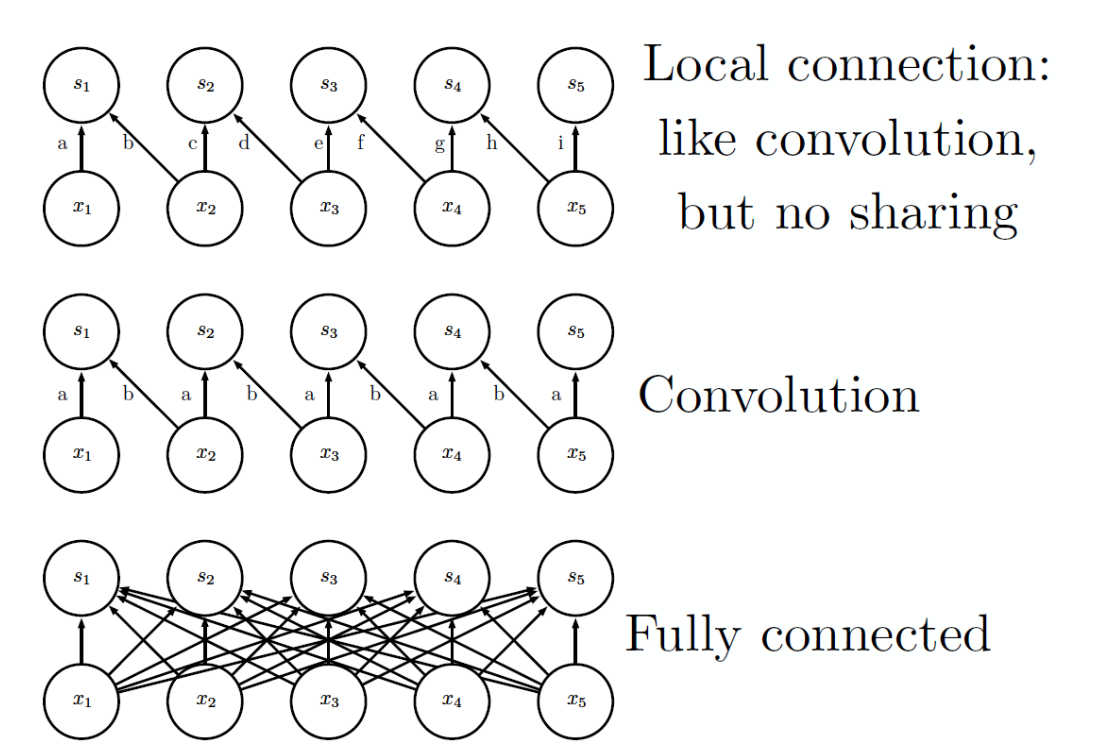

이 경우 각 위치마다 별개의 필터(파라미터)가 연결되므로 위치에 따른 지역적 특징을 추출하는 데 효과적이지만, 일반적인 합성곱 연산에 비해 연산량이 커진다.

Tiled convolution

이는 필터를 몇 가지 그룹으로 나누어 각 그룹에 속한 필터는 특정 영역에서만 공유되는 방식이다.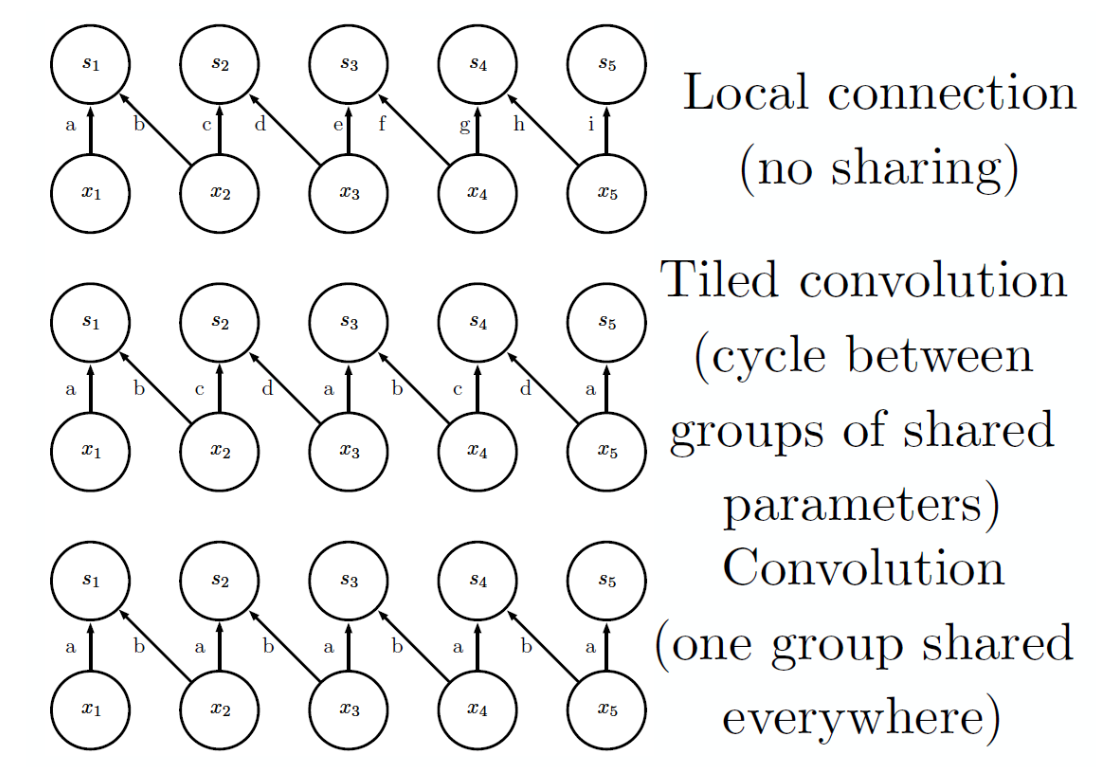

완전한 파라미터 공유보다 유연하고, 지역 특징을 더 세분화해서 학습할 수 있다는 장점이 존재한다.

CNN Architectures

CNN은 효율적인 네트워크인 동시에 높은 정확도를 달성 할 수 있는 아키텍처이다.

대표적인 CNN 아키텍처들에 대해 살펴보자.

LeNet(1998)
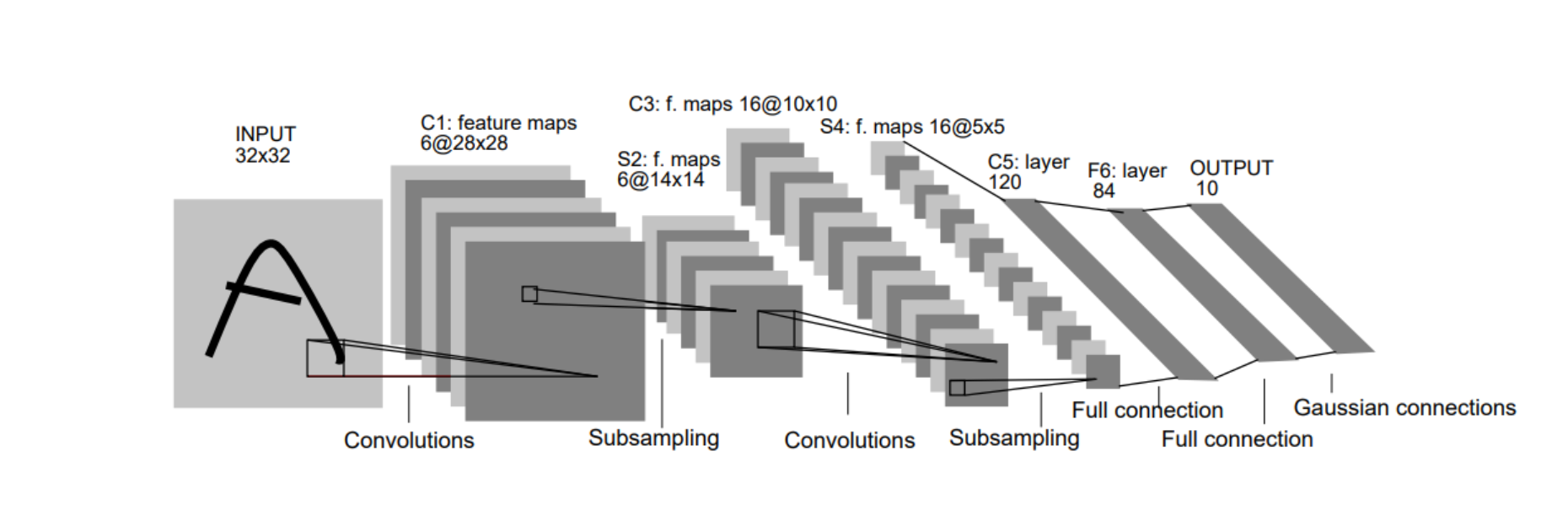
AlexNet(2012)
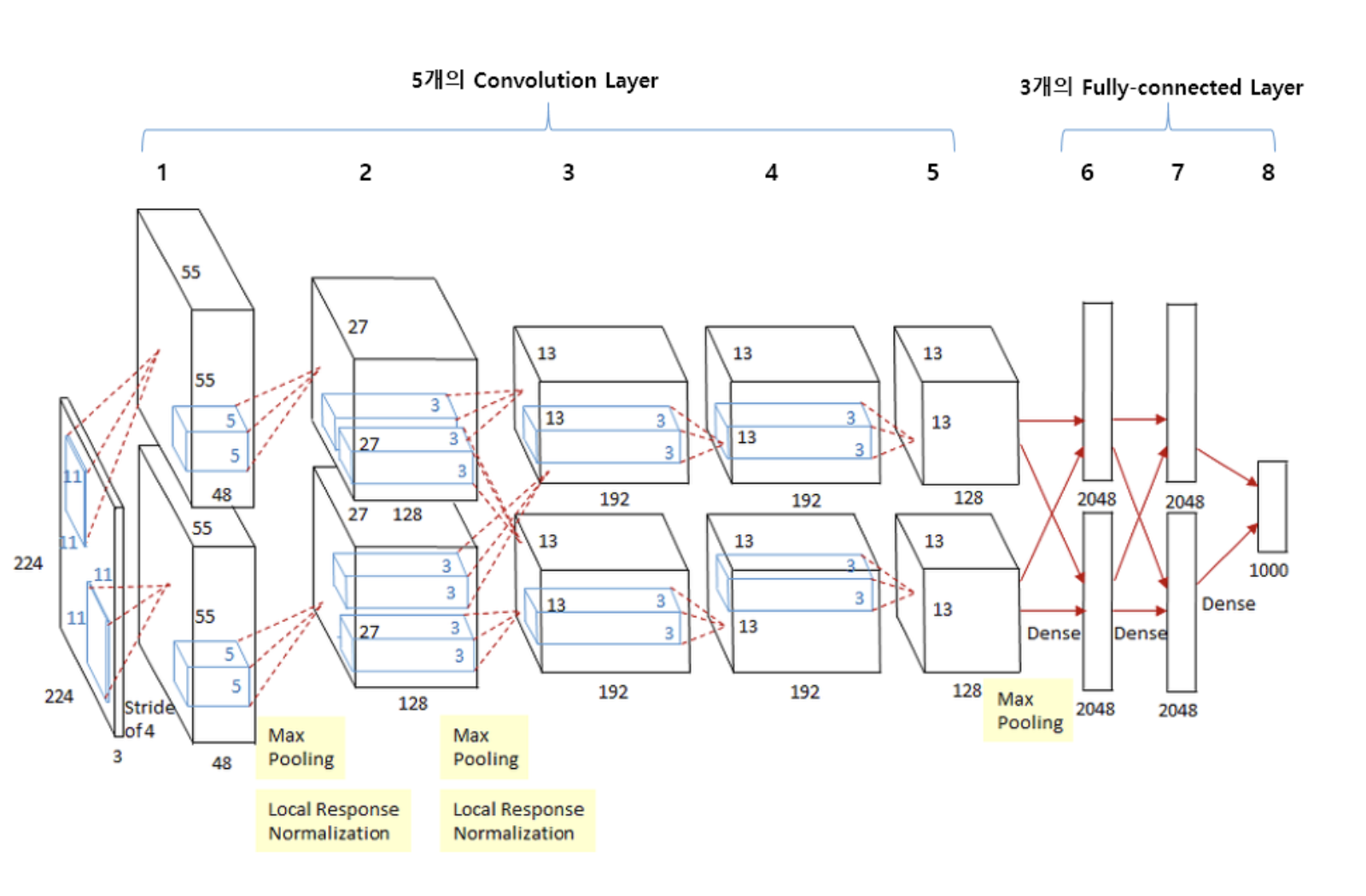
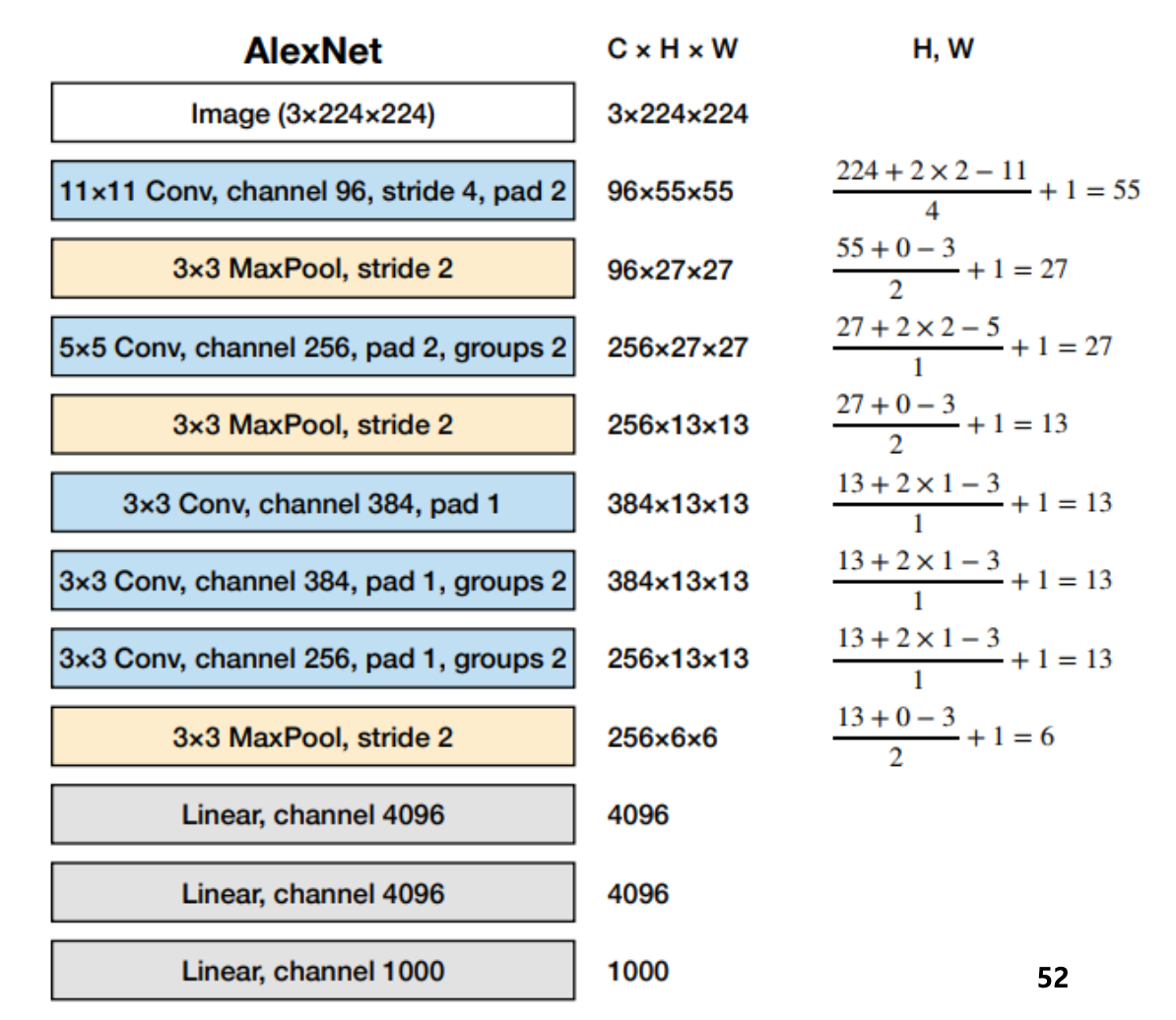
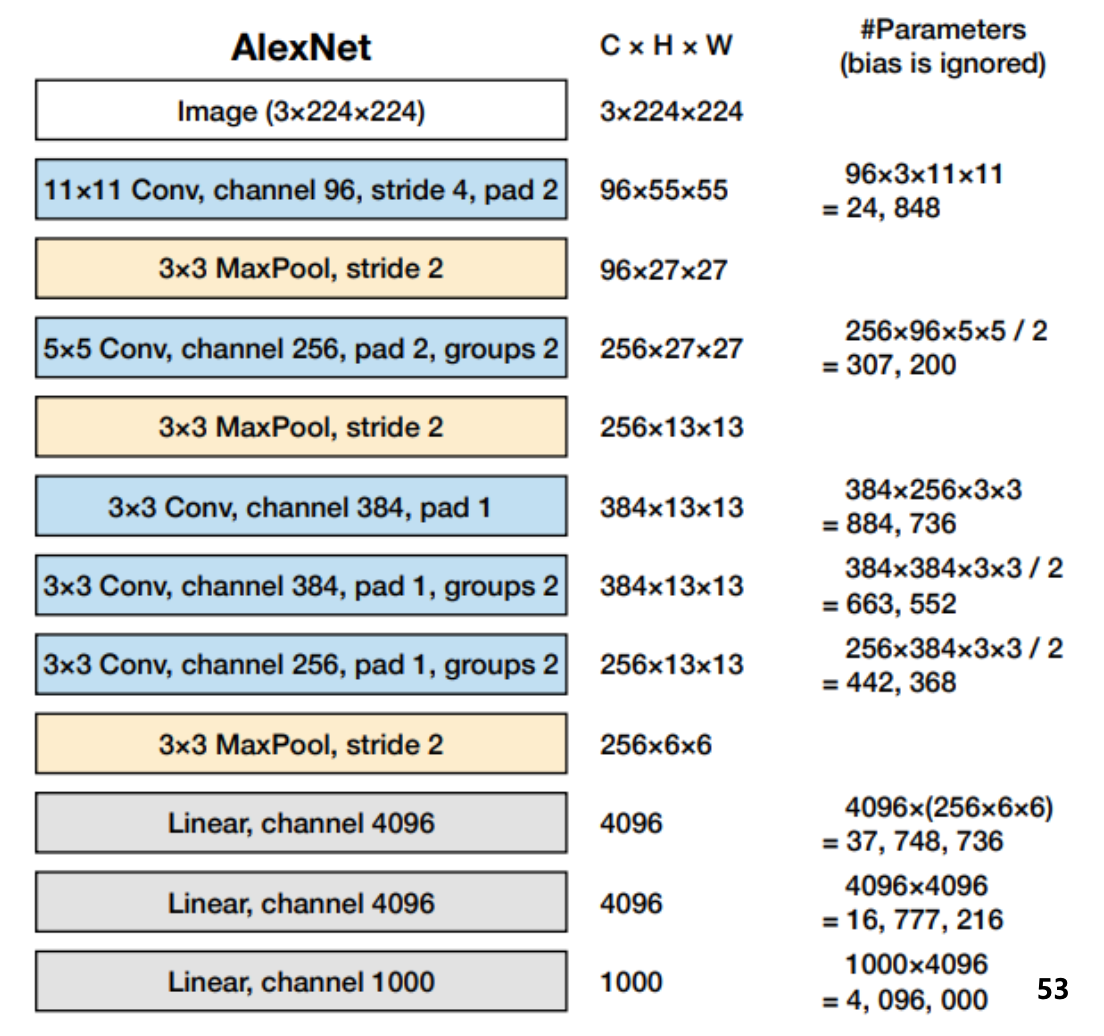
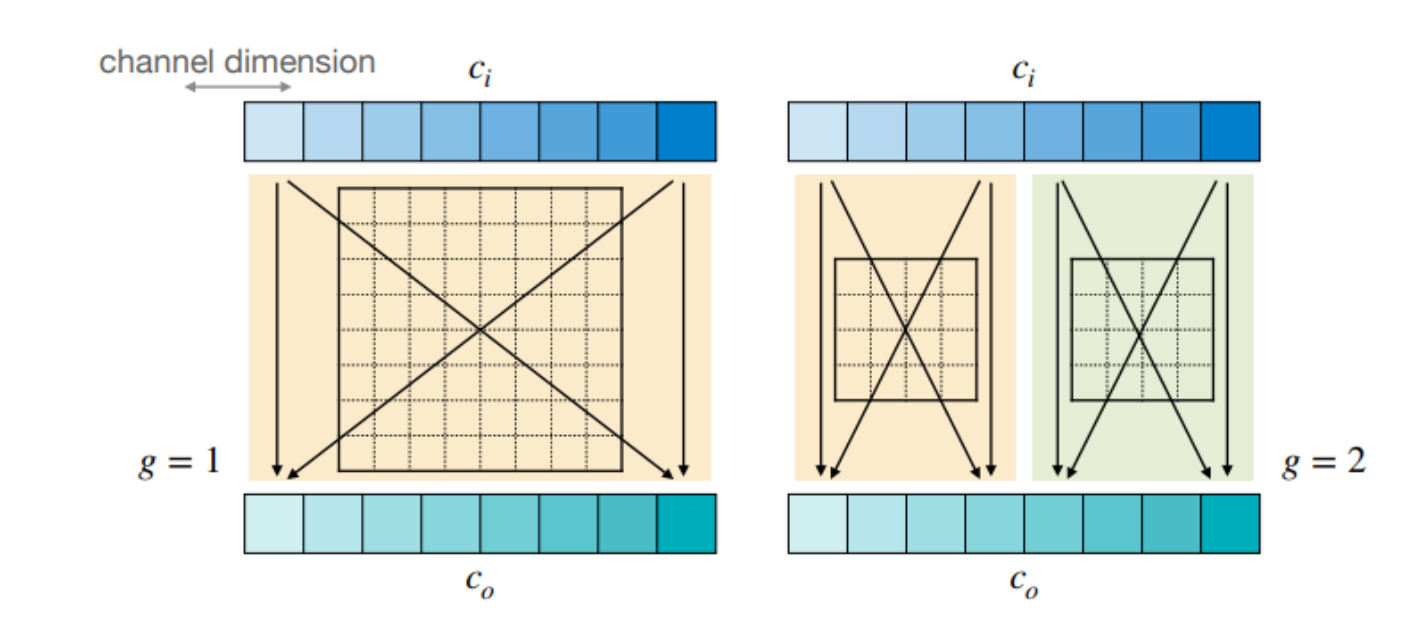
- 2개의 GPU로 병렬 연산을 수행하기 위해 병렬적인 구조로 설계 (Grouped convolution layer)
VGGNet(2014)
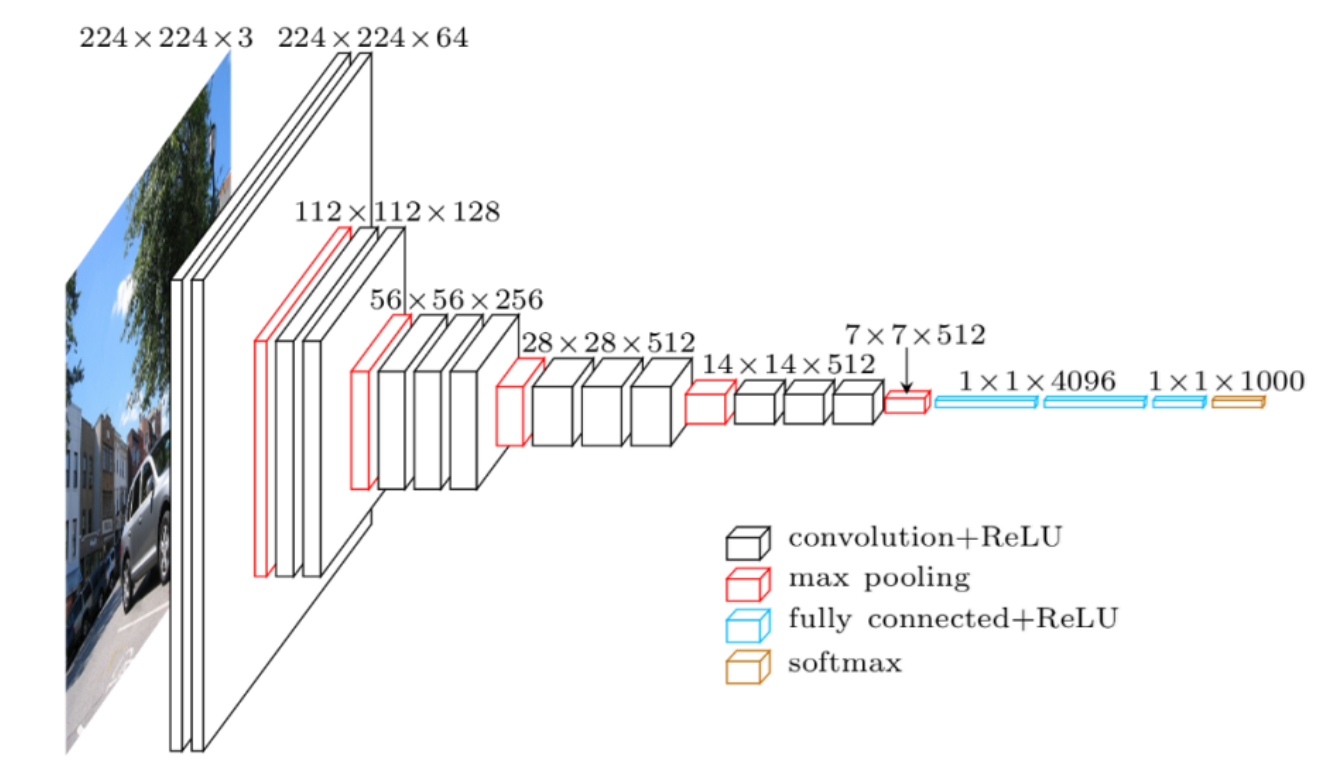
VGG-16(2014)
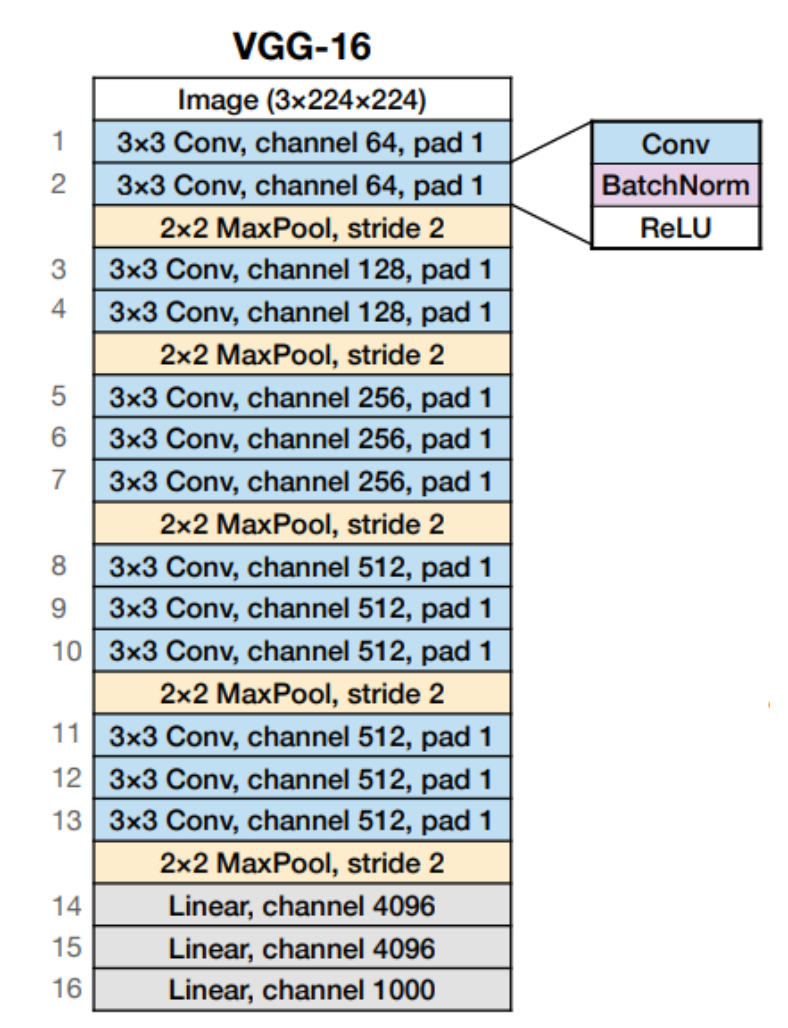
GoogleNet(2014)
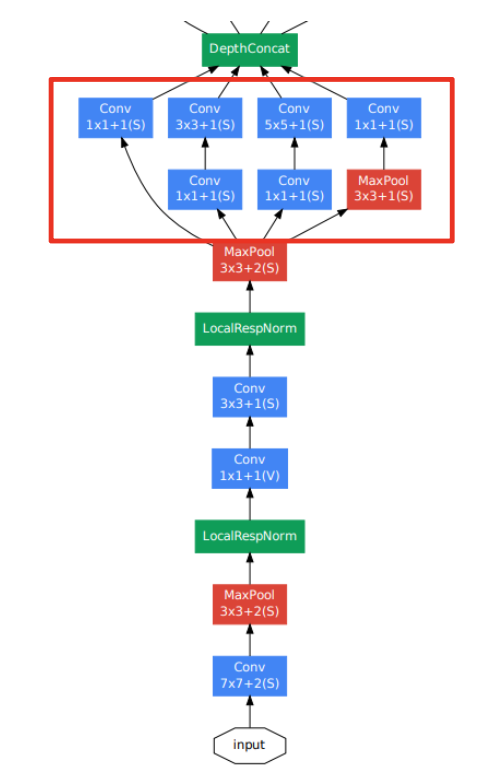
- Inception module : 다양한 종류의 필터를 활용해 추출한 여러 종류의 feature map들을 결합하면서 보다 풍부한 특징 추출이 가능

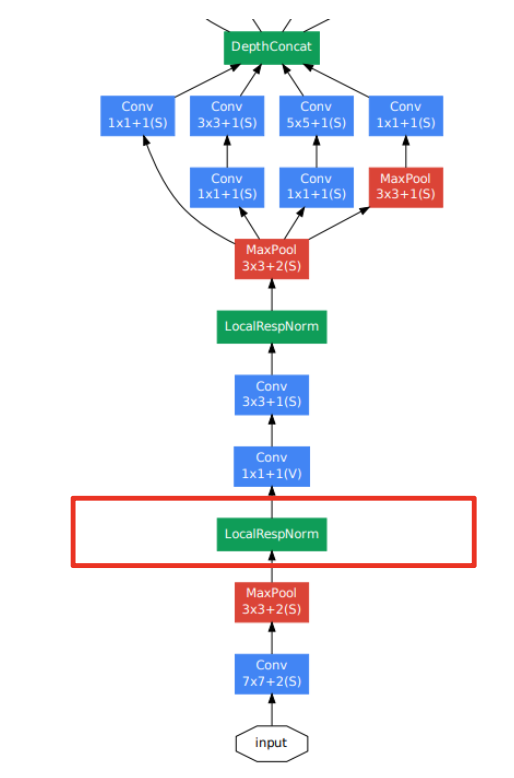
LRN(Local Response Normalization) : 동일한 위치를 공유하는 인접 채널의 뉴런들 간 정규화를 통해 특정 채널의 높은 활성화를 억제하는 기법
ResNet(2015)
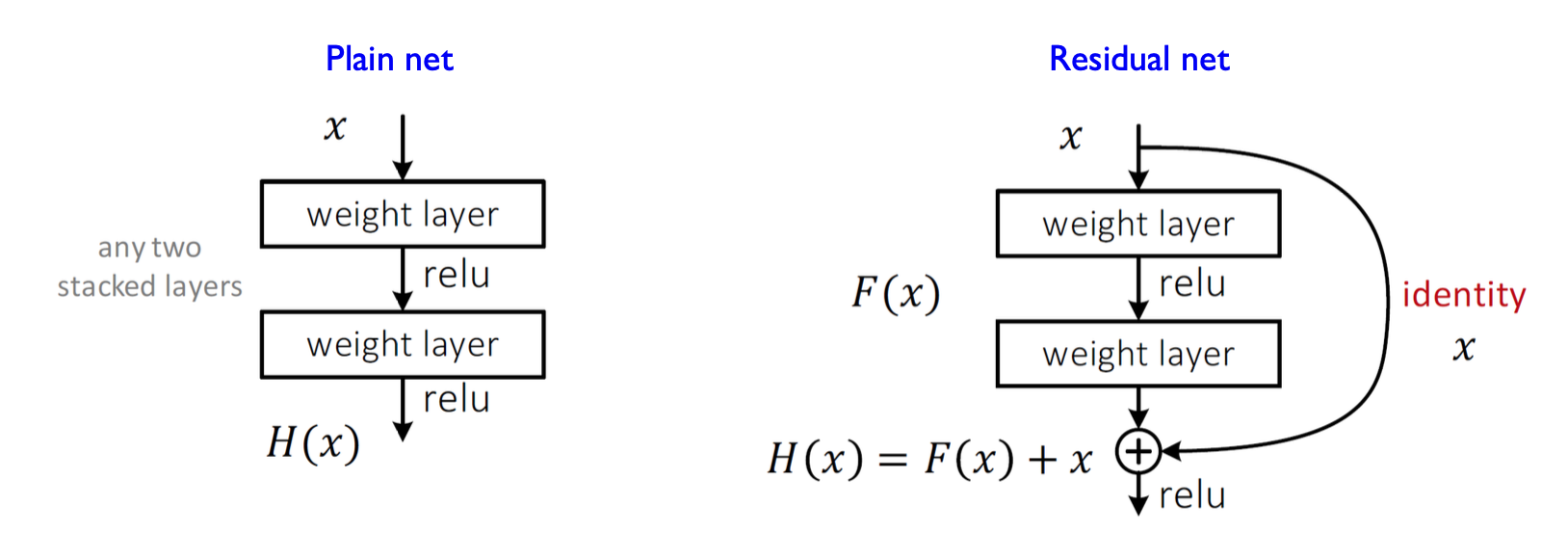
- Skip connection : 입력을 그대로 다음 층에 전달함으로써, 층의 입력을 다음 층에 직접 전달해주는 기법이다.
  - 이는 Gradient vanishing/exploding 문제를 완화할 수 있다.
  - 입력 정보를 계속 보존할 수 있어 학습의 안정성과 빠른 수렴을 유도한다.
ResNet-50(2016)
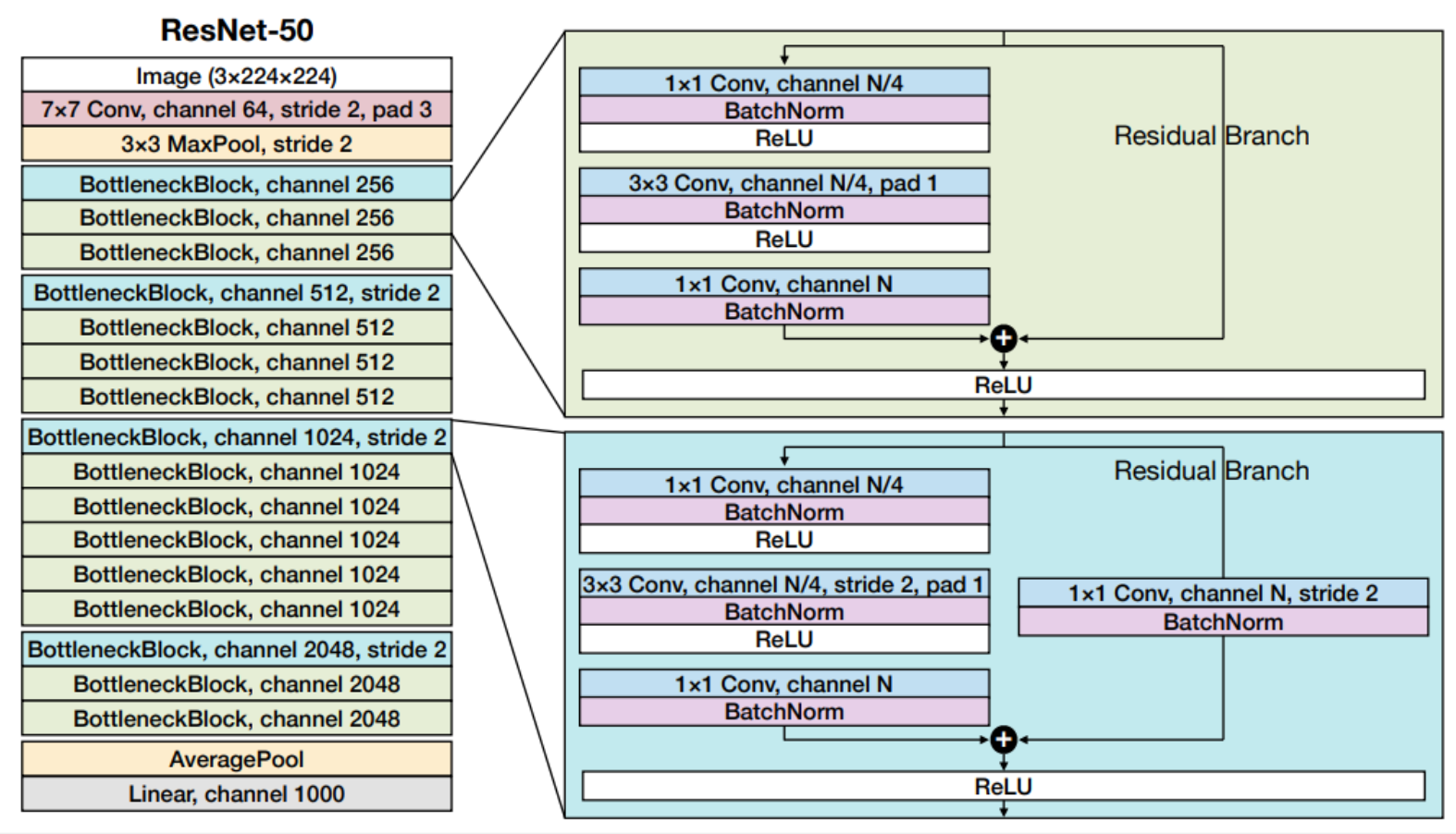
DenseNet
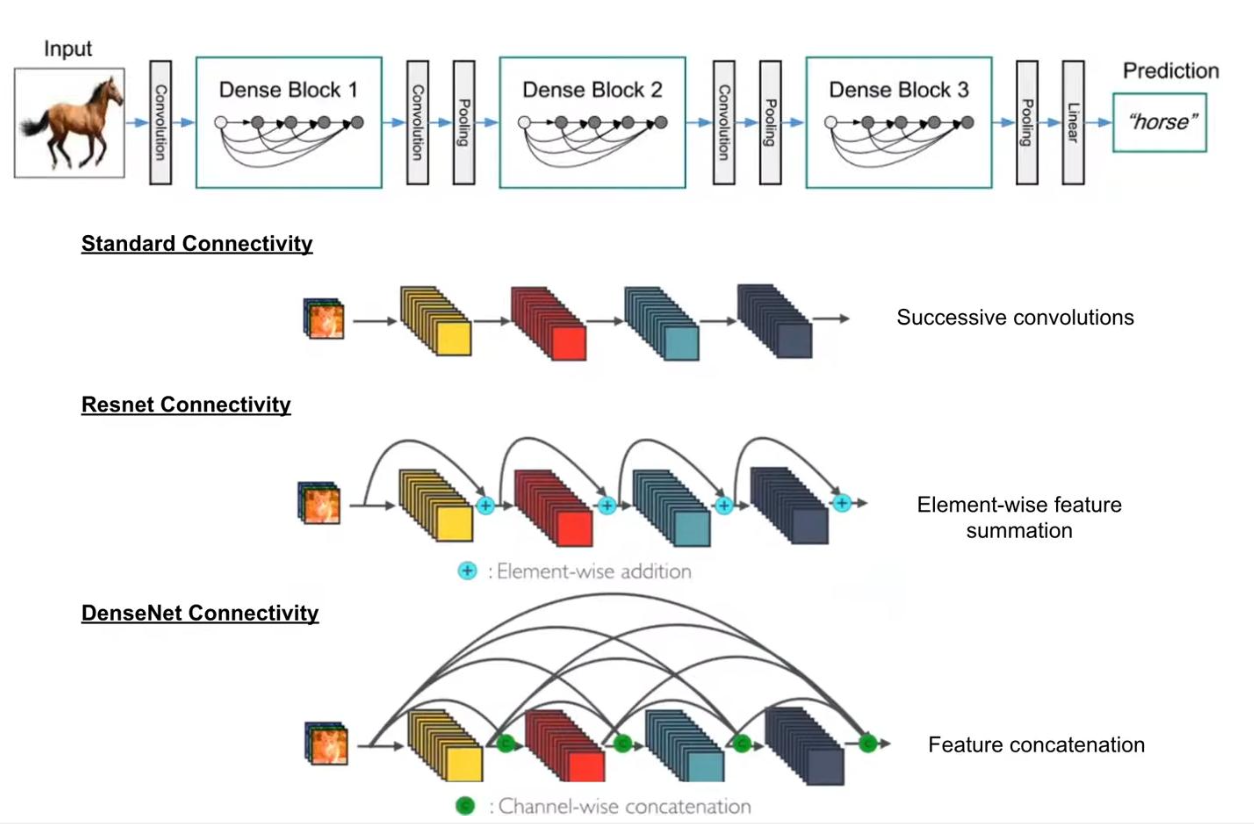
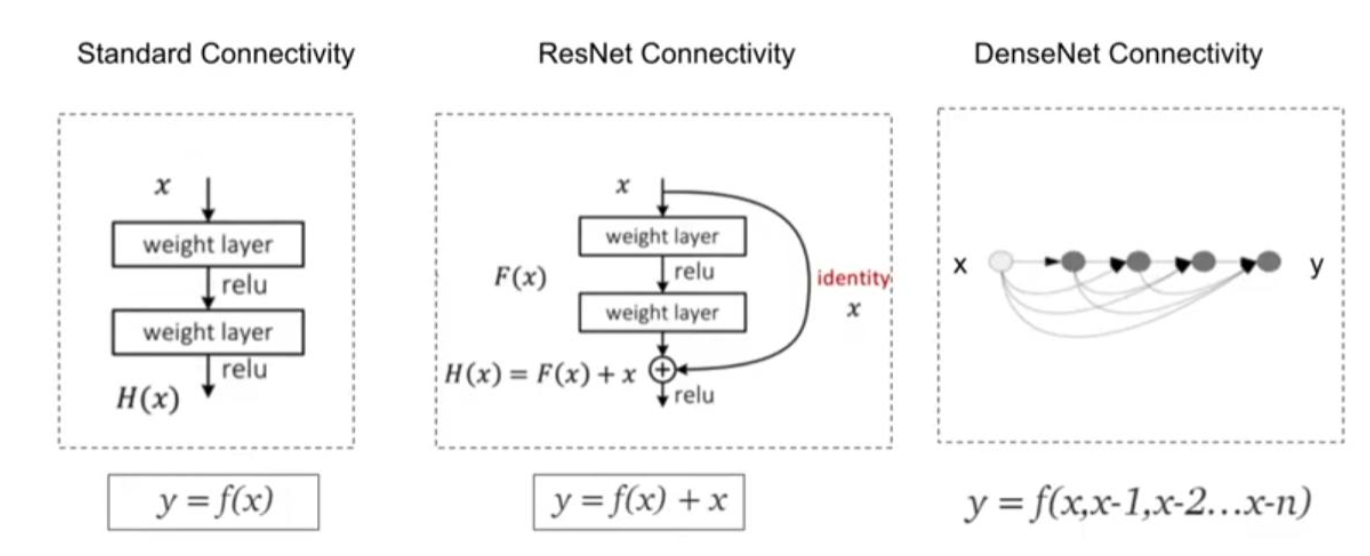
- Dense connectivity : DenseNet은 각 층의 출력을 이후의 모든 층에 직접 연결하는 구조를 가진다.
  - Avoid vainshing gradient : 이는 사라지는 기울기 문제를 완화할 수 있다.
  - Feature reuse : 이전 층의 특징을 매번 새로 계산하지 않고 그대로 다시 사용하므로 계산 효율성이 높고 정보 손실이 최소화 됨.