[Deep Learning] Chapter 5 - Regularization and Optimization

Regularization

머신러닝의 목표는 학습을 통해 일반화 능력이 좋은 모델을 만드는 것이다.

Regularization(정규화)란, 일반화 성능을 높이기 위해 과적합을 방지하는 기법이다.

적절한 파라미터와 깊이를 갖는 모델을 찾았다고 해서 모델의 복잡도를 완벽하게 제어하고 있는 것은 아니다.

특히, 딥러닝에서는 적절한 정규화를 거친 Large Model이 훨씬 우수한 성능을 보인다는 것이 알려져 있다.

정규화의 핵심 아이디어들은 다음과 같다.

• Objective function(목적 함수)에 Constraints(제약)이나 Terms(항)을 추가하여 모델 복잡성을 억제

• 사전 지식 활용(prior knowledge)

• 더 단순한 모델 설계(불필요한 파라미터 제거)

• 앙상블 기법(Ensemble method)

Parameter regularization

파라미터 정규화는 모델의 복잡성을 제한하기 위해 목적 함수에 Norm-penalty 항을 추가하는 형태의 정규화 기법이다.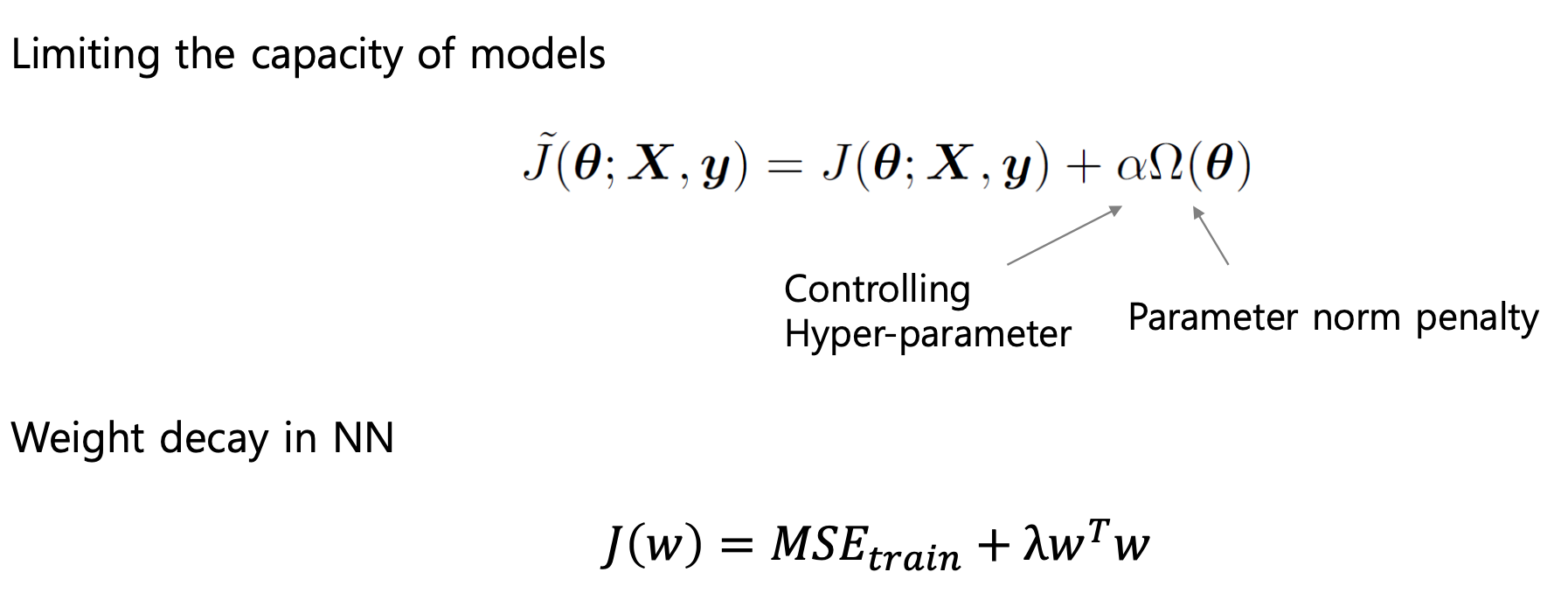

L2-Norm penalty

L2-Norm penalty는 가장 일반적으로 사용되는 가중치 정규화 방식으로, 다음과 같이 정의한다.

여기서 $||w||^2_2$는 가중치 벡터(파라미터)의 모든 원소를 제곱해서 더한 값이다. 즉,

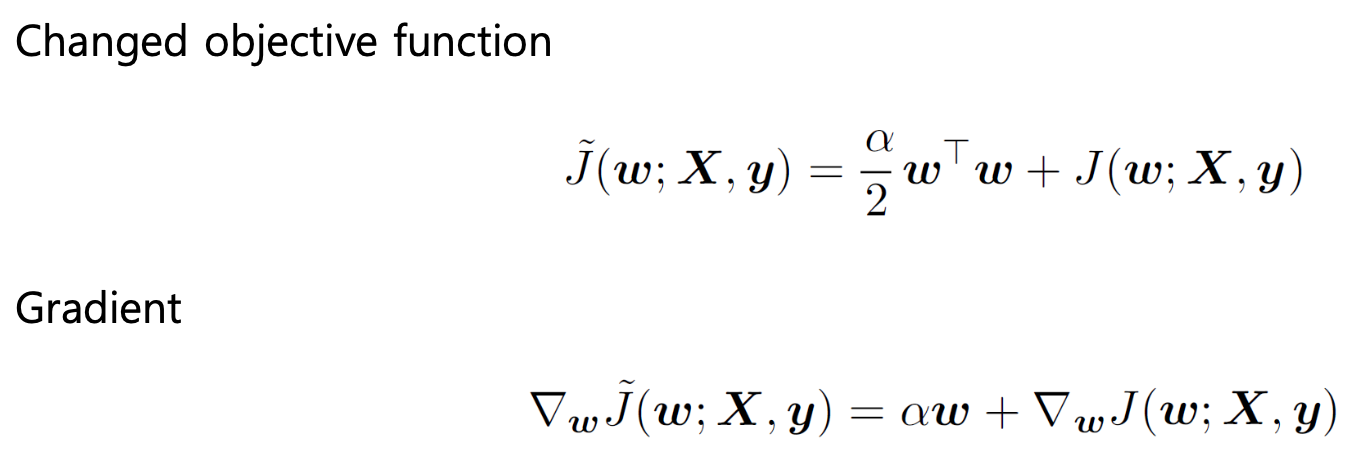
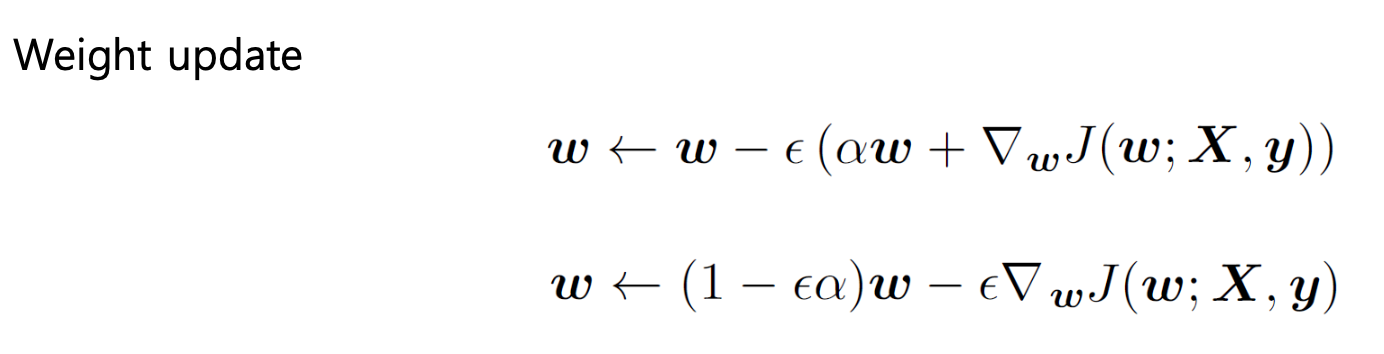
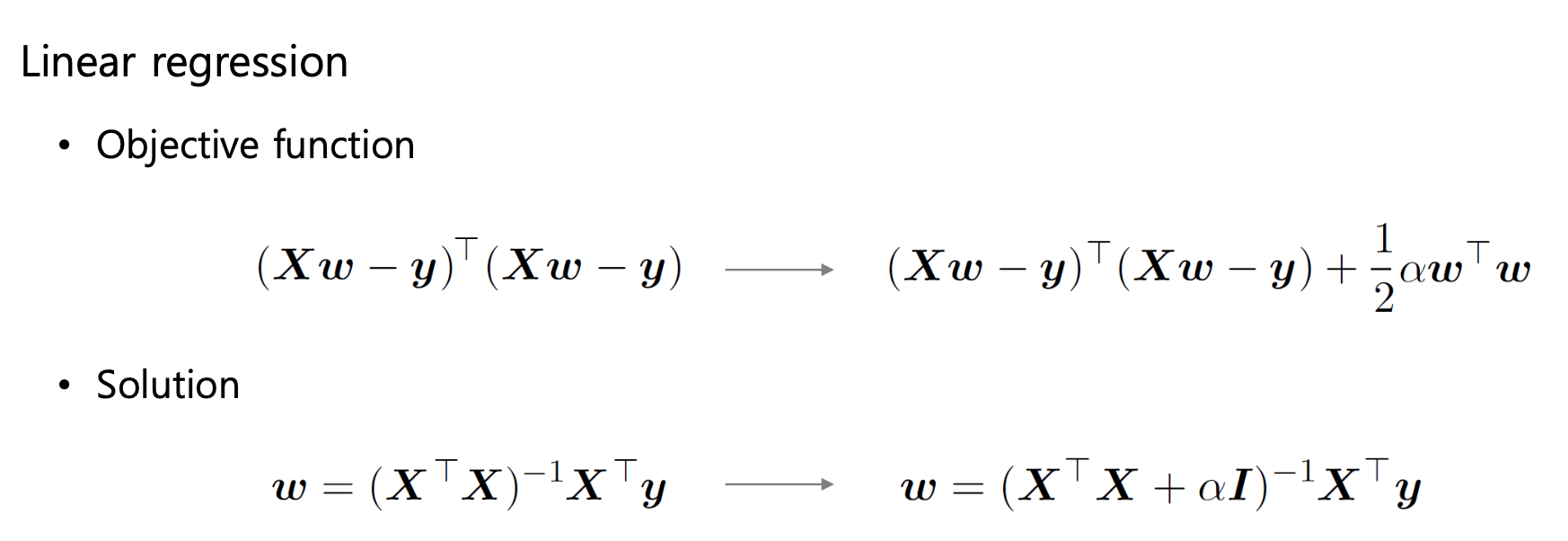
L1-Norm penalty

L1-Norm penalty는 다음과 같다.

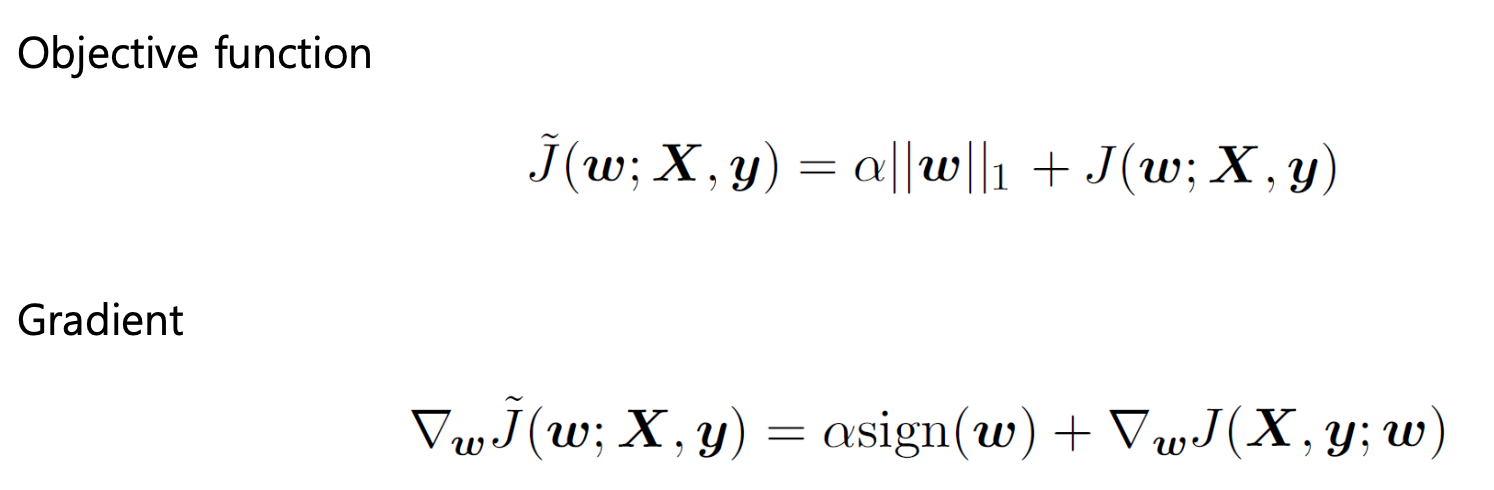
Data augmentation

머신러닝에서 많은 학습 데이터를 확보하는 것은 모델 성능에 큰 영향을 미친다.

이미 확보한 데이터셋에 변형(이동/회전/확대/축소 등)을 거쳐 추가적인 학습 데이터를 생성하는 것을 Data augmentation(데이터 증강)이라고 한다.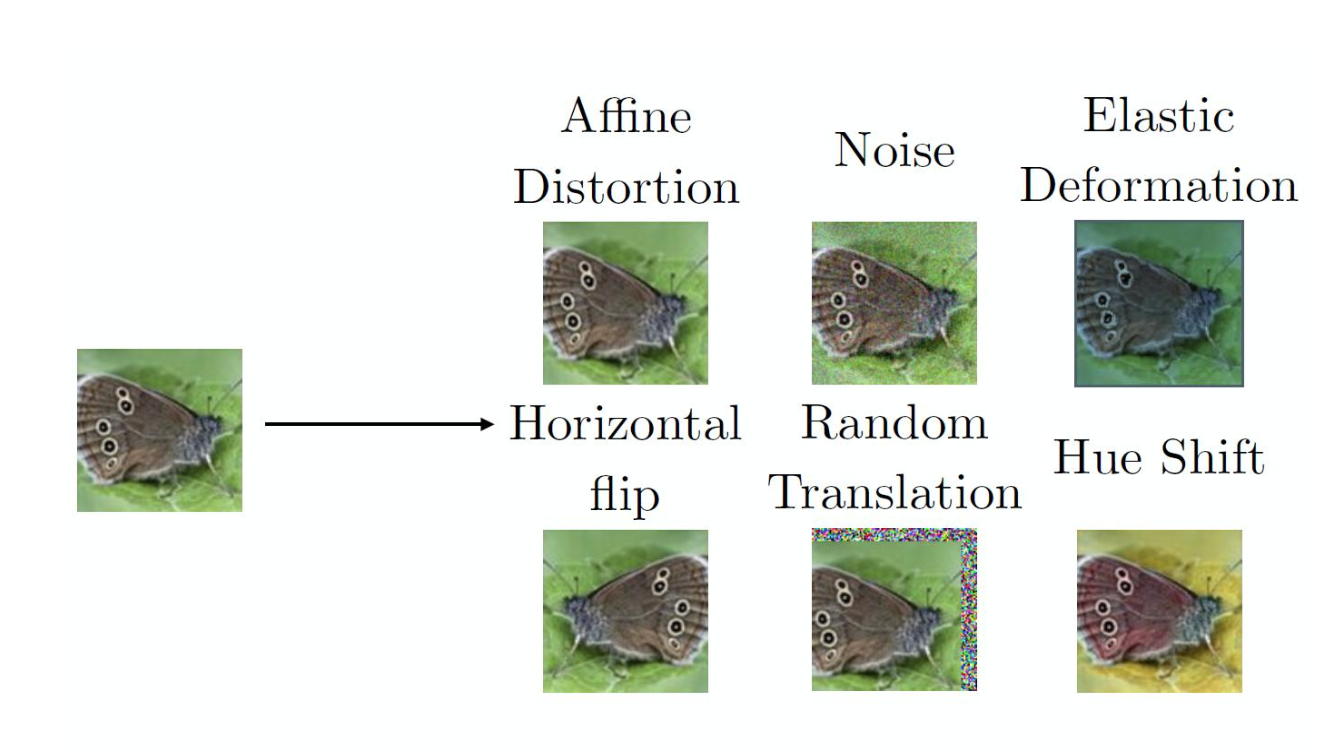

데이터 증강을 통해 모델의 일반화 성능이 향상될 수 있다.

예시로 이미지 분류 문제와 같은 경우를 살펴보자.

• 입력 $x$는 복잡하고 높은 차원

• 출력 $y$는 하나의 단순한 레이블

• 입력 데이터가 다양하게 변화(Variation)되더라도, 불변성(Invariant)이 보장되어야 한다.

  • 고양이 이미지의 형태가 변하더라도 고양이로 분류해야 함

• 따라서 학습셋에 존재하는 $x$를 변형시켜 새로운 $(x^{\prime},y)$를 생성

  • 고양이 이미지를 변형시켜 학습시키면, 형태가 다른 고양이 이미지도 잘 분류할 수 있을 것

Noise robustness

입력에 미세한 노이즈(분산이 매우 작은 노이즈)를 추가하는 기법을 Noise robustness라고 한다.

입력에 노이즈를 추가하는 것은 Norm-penalty를 추가하는 것과 유사한 효과를 가지며, 이를 통해 모델의 과적합을 방지할 수 있다.

노이즈는 여러가지 방식으로 추가할 수 있다.

• 입력 데이터에 노이즈 추가

• 은닉 유닛에 노이즈 추가(드랍아웃과 유사)

• 가중치에 노이즈를 추가

Multitask learning

Multitask Learning은 여러 작업(Task)에서 생성된 예제들을 결합(Pooling)하여 일반화 성능을 향상시키는 기법이다.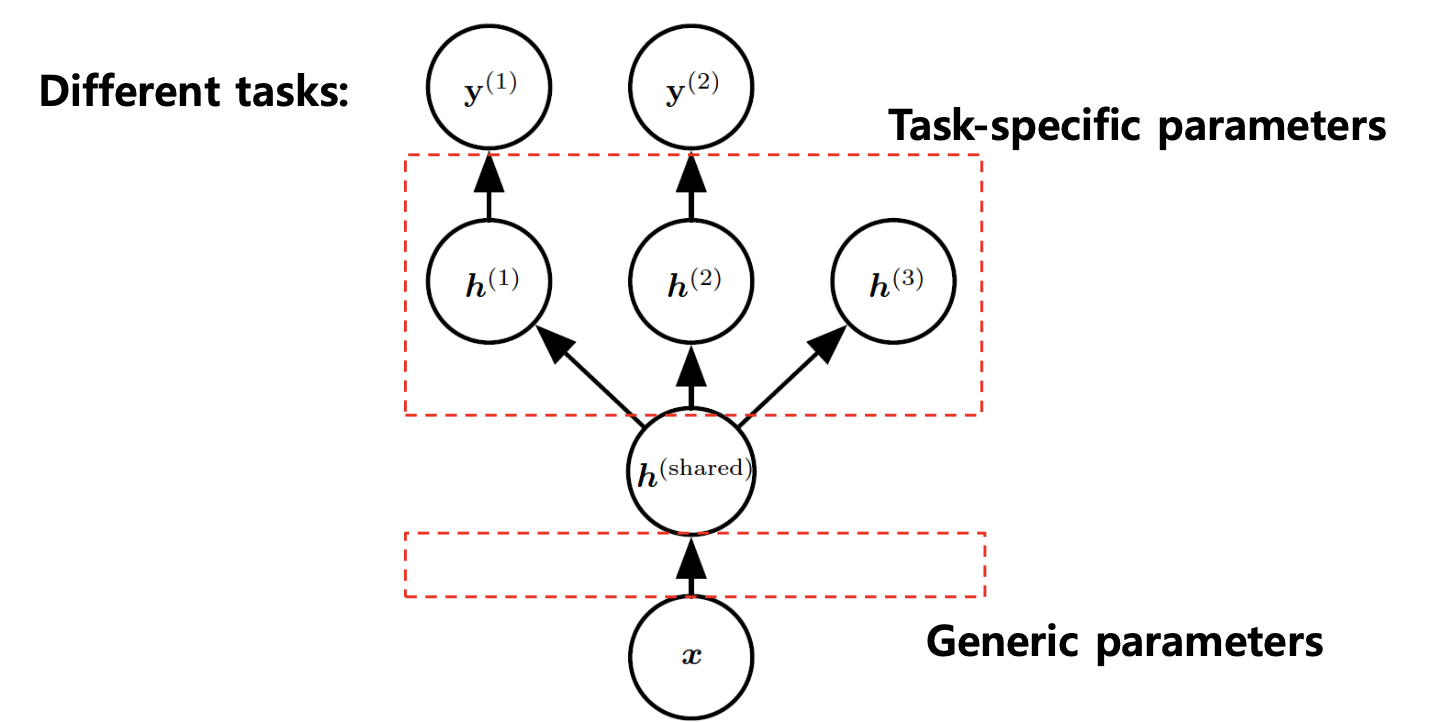

Early stopping

Validation Loss는 어느 시점부터 더이상 개선되지 않거나, 오히려 악화될 수도 있다. 이는 과적합의 신호일 수 있기 때문에, 학습을 조기에 중단(Early stopping)하는 기법이 사용되기도 한다.

따라서 조기 종료는 검증 성능이 가장 좋은 시점에서 학습을 중단하여 일반화 성능이 가장 높은 모델을 확보하는 방식이다.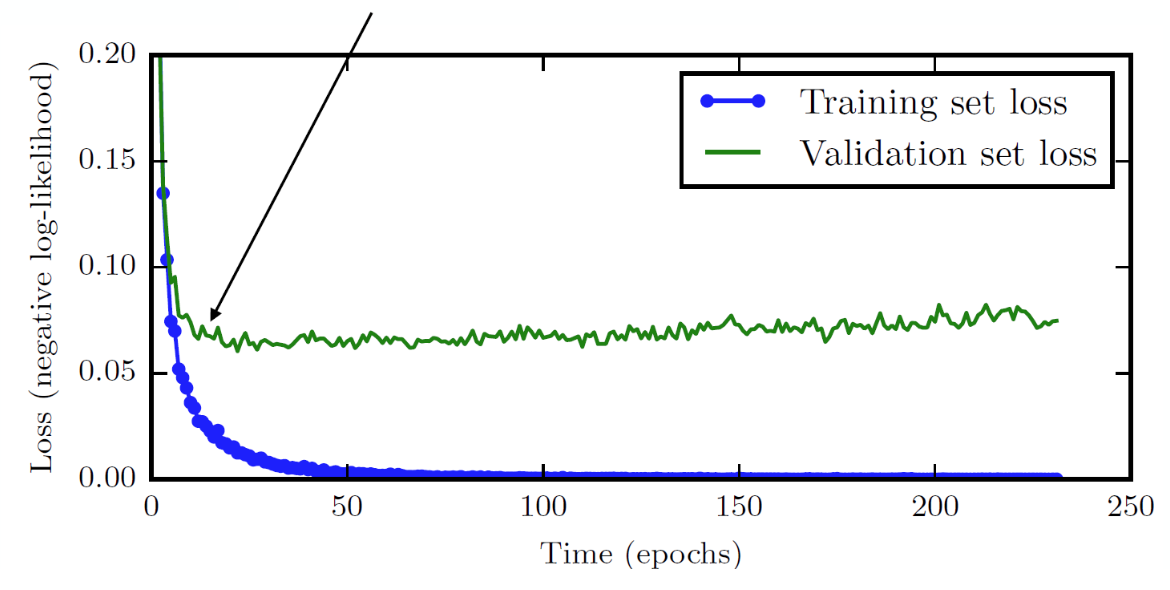

Parameter tying and sharing

우리는 어떤 파라미터가 정확히 어떤 값을 가져야 하는지는 모르지만, 동일한 작업을 수행하는 각 파라미터들은 서로 어떠한 의존성이 존재해야 한다는 것은 알고 있다.

Parameter tying

우리는 약간 다른 입력 분포를 갖지만 동일한 분류 작업을 위한 두 모델 $(A, B)$를 갖고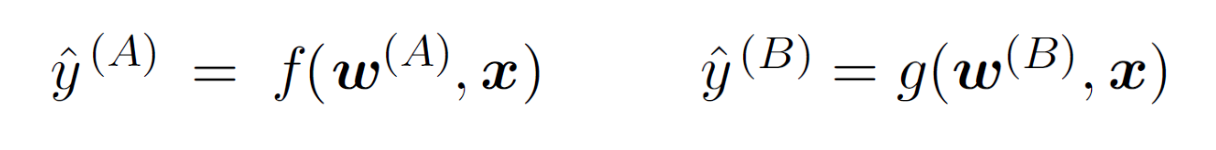 있다.

우리는 모든$i$에 대해 $w_i^{(A)}$와 $w_i^{(B)}$는 서로 관계성이 있는 파라미터라는 것을 알기 때문에 정규화 항을 다음과 같이 정의할 수 있다.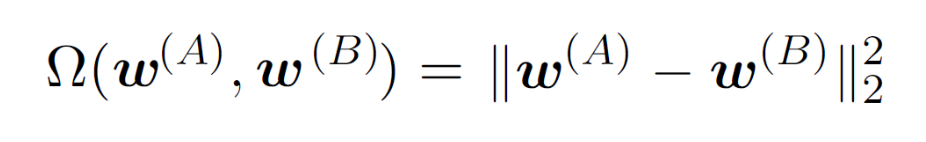

우리는 동일한 작업을 수행하는 두 모델은 각 파라미터 간 거리가 그렇게 멀지 않다는 것을 직관적으로 이해할 수 있으며, 따라서 두 모델의 파라미터 정규화를 진행할 경우 두 모델은 거의 동일한 모델이 될 것이다.

Parameter sharing

파라미터 공유는 CNN(합성곱 신경망)의 핵심 아이디어로, 이미지 전체에 동일한 필터(동일한 파라미터)를 적용하는 방식이다.

파라미터 공유는 이미지 전체에 대해 동일한 특성을 감지하는 데 매우 적합하며, 메모리(모델 복잡성)를 줄일 수 있다는 장점이 존재한다.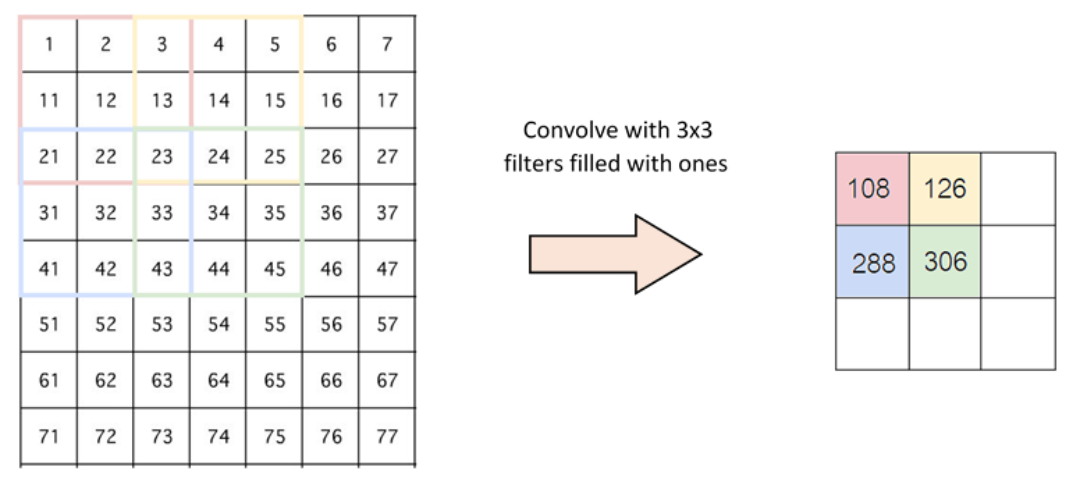

Sparse representation

Sparse representation(희소 표현)이란, 신경망 내부의 뉴런들이 모두 활성화되지 않도록 제약을 거는 정규화 기법이다.

이는 학습에 중요하지 않은 파라미터들이 존재할 수 있으므로, 이를 제한하는 방식이다.

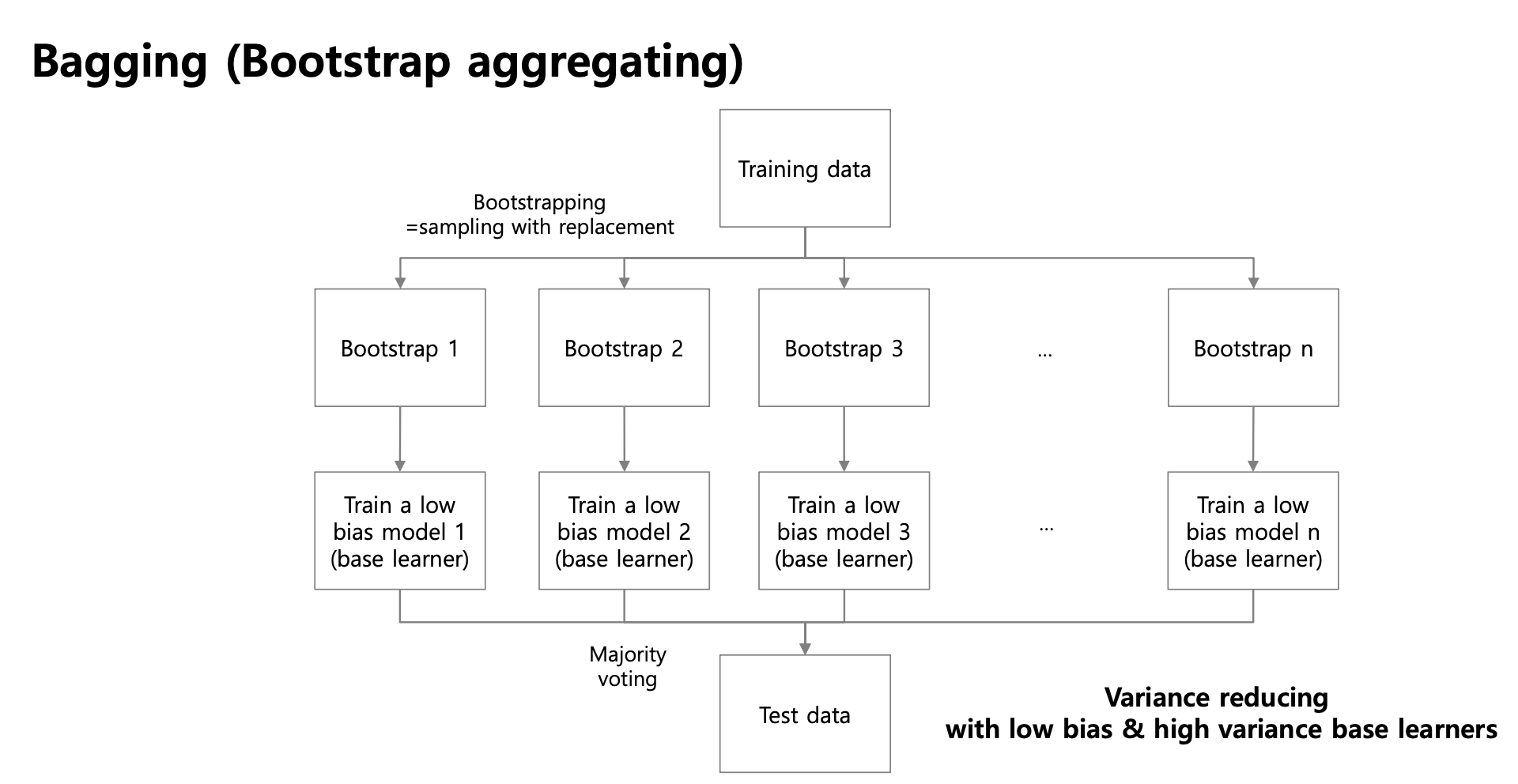
Bagging (Bootstrap aggregating)

복원 추출한 데이터를 활용해 여러 개의 모델을 학습하여 예측을 평균(다수결)하는 앙상블 기법이다.

Dropout

드롭아웃은 신경망에서 은닉층의 뉴런들을 무작위로 비활성화(Drop)하며 서브 네트워크들을 학습시키는 기법이다.

이는 마치 많은 신경망을 배깅(Bagging)해서 학습시키는 것과 유사한 효과를 가지며, 실제로는 하나의 모델을 학습하는 것이지만 매 반복마다 다른 구조의 모델을 훈련시키는 것과 동일한 효과를 갖는다.

각 서브 네트워크에서 비활성화 되는 유닛이 다르므로, 앙상블을 저렴한 방식으로 근사할 수 있다.

Dropout vs Bagging

드롭아웃은 앙상블(배깅)을 근사하지만, 실제로 여러 모델을 학습하지 않고 하나의 모델 내에서 서브 네트워크를 반복적으로 활용하는 방식이다.

Adversarial training

Adversarial Example(적대적 예제)란, 원본 입력 $x$에 아주 작은 변화를 준 새로운 입력 $x^{\prime}$을 의미한다.

입력 $x^{\prime}$와 원본 $x$은 사람의 시각에선 유사해 보이지만, 모델은 $x^{\prime}$과 $x$를 동일한 것으로 분류하지 못할 수 있다.

즉, 모델은 데이터의 분포에 따라 학습하여 분류하기 때문에, 사람이 비슷하다고 느끼는 것과 모델이 비슷하다고 분류하는 것은 다를 수 있다.

의도적으로 적대적 예제를 학습 데이터로 사용하여 모델의 강건성을 강화시키는 학습 방식을 Adversarial training이라고 한다.

Optimization

전체 학습 데이터에 대해 비용 함수 $J(\theta)$를 최소화하는 신경망 파라미터 $\theta$를 찾는 것이 최적화의 목표이다.

비용 함수 $J(\theta)$는 일반적으로 Loss + Regularization term로 구성된다.

Difference from pure optimization

신경망의 최적화와 순수한 의미의 최적화(Pure optimization)은 구분해서 이해해야 한다.

우리는 성능 $P$를 개선하기 위해 비용 함수 $J(\theta)$를 최소화하는 간접적인 방식을 택한다. 하지만 비용 함수의 최소화가 항상 성능 향상을 보장하지는 않는다.

이와 달리 순수한 의미의 최적화는 비용 함수 $J(\theta)$ 자체를 최적화하는 것을 목표로 한다.

우리는 훈련 데이터 분포 $\hat{p}_{data}$를 사용해 학습한 모델을 최적화 하기위해 비용 함수를 최적화한다.

하지만 사실 원하는건 실제 데이터 분포 $p_{data}$를 사용한 모델의 최적화이다.

즉, 두 비용 함수는 근사 관계에 불과하며, 우리는 실제 데이터의 생성 분포를 알지 못한다.

우리는 실제 데이터에 대한 성능이 최적화되길 바라며 훈련 데이터(empirical data)로 훈련된 모델에 대해 최적화(risk minimize)를 진행한다. 이를 Empirical risk minimization(경험적 위험 최소화)라고 한다.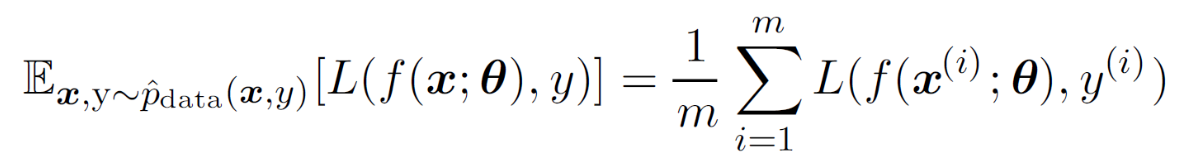

모델은 훈련 데이터를 그대로 암기(Memorize)할 수 있으므로, 경험적 위험 최소화는 모델의 일반화 능력을 보장하지 못한다.

Batch and Minibatch Algorithms

전체 데이터셋에 대한 최적화는 비용이 많이 드는 작업이다.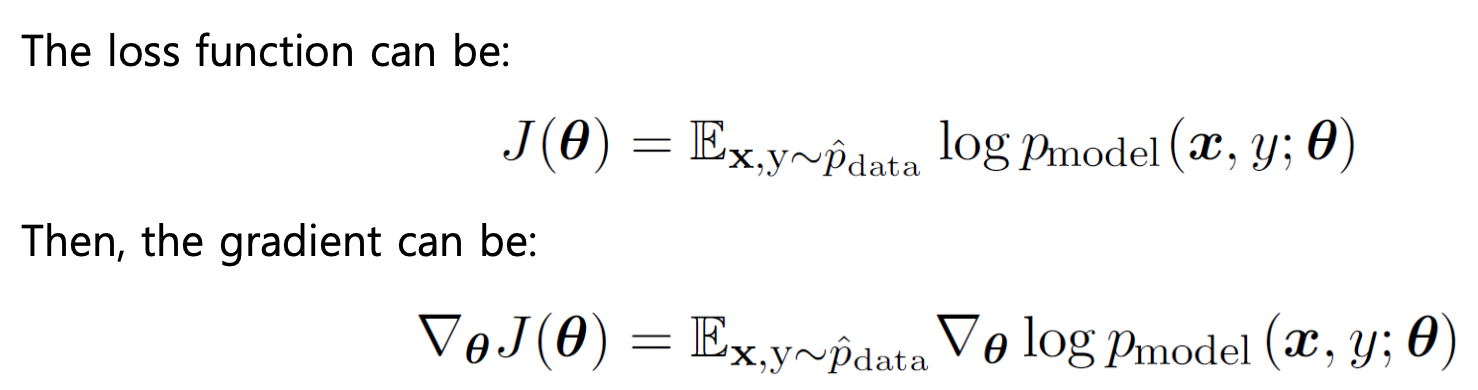

작은 일부 샘플만으로 빠르게 기울기(Gradient)를 계산하여 이를 활용할 수 있다.

근사적인 추정(통계학의 표본 집단을 생각해보자)을 통해 우리는 일부 샘플이 전체 데이터셋과 유사한(동일한) 분포를 갖는다고 가정할 수 있다.

• Batch(Deterministic, 결정론적) : 전체 훈련 데이터셋을 이용해 최적화 수행

• Online(Stochastic, 확률적) : 오직 하나의 데이터셋 샘플을 이용해 최적화 수행

Minibatch(Stochastic) 방식은 배치와 온라인을 섞은 방식으로, 1(onlie) < size < batch 범위에 속하는 batch size를 선택하여 최적화를 수행하는 방식이다.

Minibatch size

• Larger : 정확도가 높지만, 비용이 많이 듦

• Smaller : 정규화 효과가 있지만, 더 많은 스탭이 필요

미니배치를 활용해 일반화된 손실 함수를 얻기 위해선, 추출된 데이터셋 샘플의 데이터들이 중복되지 않고 독립성을 가져야 한다.

훈련 데이터는 유사하거나 중복된 샘플이 있을 수 있기 때문에, 매 에폭마다 셔플링(shuffling)을 통해 미니배치가 데이터 분포를 잘 대표하도록 해야 한다.

Challenges in NN Optimization

신경망 최적화를 어렵게 만드는 여러 문제들이 존재한다.

• Ill-conditioning(비정상적 조건) : Condition Number란, 입력의 변화에 따른 출력의 변화를 수치적으로 표현한 것이다.

  • Condition Number가 크다는 것은 비정상적으로 민감한 시스템이라는 것이며, 이를 Ill-conditioning이라고 한다.

• Local Minima (지역 최적점) : 현재는 대규모 신경망의 경우 Local Minima들도 충분히 최적점에 근사한다고 가정하지만, 여전히 지역 최적점에 갇히는 문제가 존재할 수 있다.

• Saddle points : Saddle points는 극값처럼 보이지만 한 방향에서는 최솟값, 다른 방향에서는 최댓값이 되는 지점이다.

  • DNN의 손실 함수는 고차원 공간 위에 정의되므로 이러한 Saddle points가 지역 최적점보다 자주 등장한다.

• Cliffs : 손실 함수가 급격히 떨어지는 지형이 존재할 경우, Gradient가 과하게 커져 파라미터가 한번에 많이 갱신되어 이후 단계에선 최적점이 아닌데도 Gradient가 거의 갱신되지 않을 수 있다.

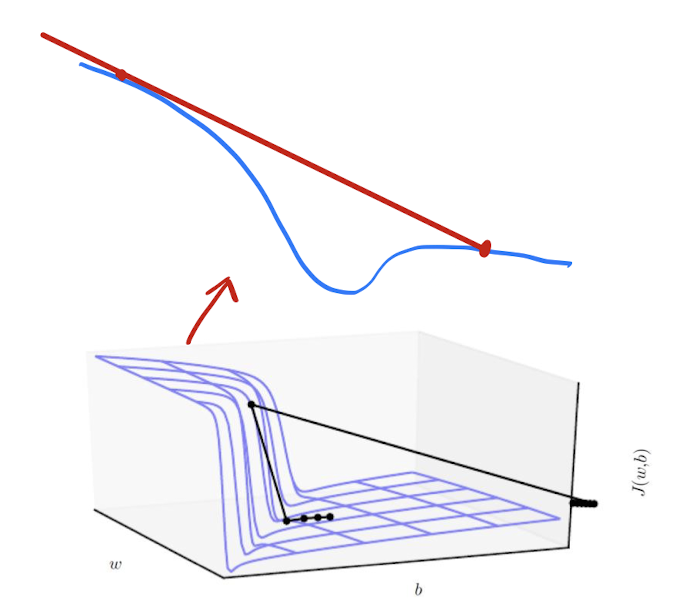
• Long-term dependencies(사라지는 혹은 폭발하는 기울기) : 역전파 과정에서 그래디언트가 점점 작아지거나 커지면서 학습이 제대로 이루저지지 않는 문제이다.

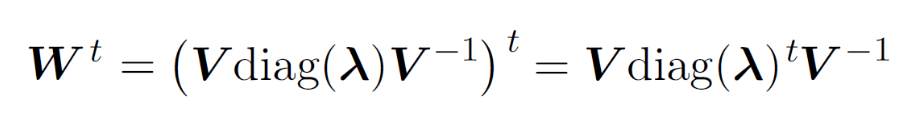
Optimization Algorithms

Stochastic Gradient Descent(SGD)

Stochastic Gradient Descent(SGD, 확률적 경사 하강법)은 딥러닝에서 가장 흔하게 사용되는 최적화 기법이다.

SGD를 활용할 때, 미니배치는 데이터 생성 분포로부터 서로 독립적이고 동일한 분포로 추출되어야 한다.

SGD는 각 에폭마다 무작위 샘플링을 진행하기 때문에, 항상 약간의 노이즈 요인(불확실성)을 포함하고 있다고 볼 수 있다. 따라서 학습률 $\epsilon$은 SGD에서 매우 중요한 하이퍼파라미터이다.

• Batch Gradient Descent : 학습률 고정

• SGD : 반복 횟수 $k$에 따라 학습률 감소

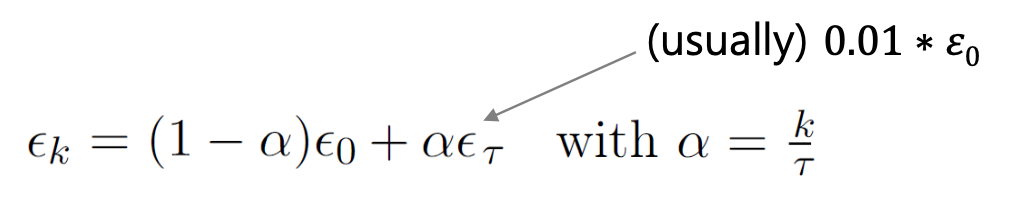
Momentum

Vanishing Gradient 문제를 해결하기 위해 고안된 기법으로, 과거 그래디언트의 누적을 반영한 추가적인 이동을 유도함으로써 빠르게 최적화가 이루어지도록 한다.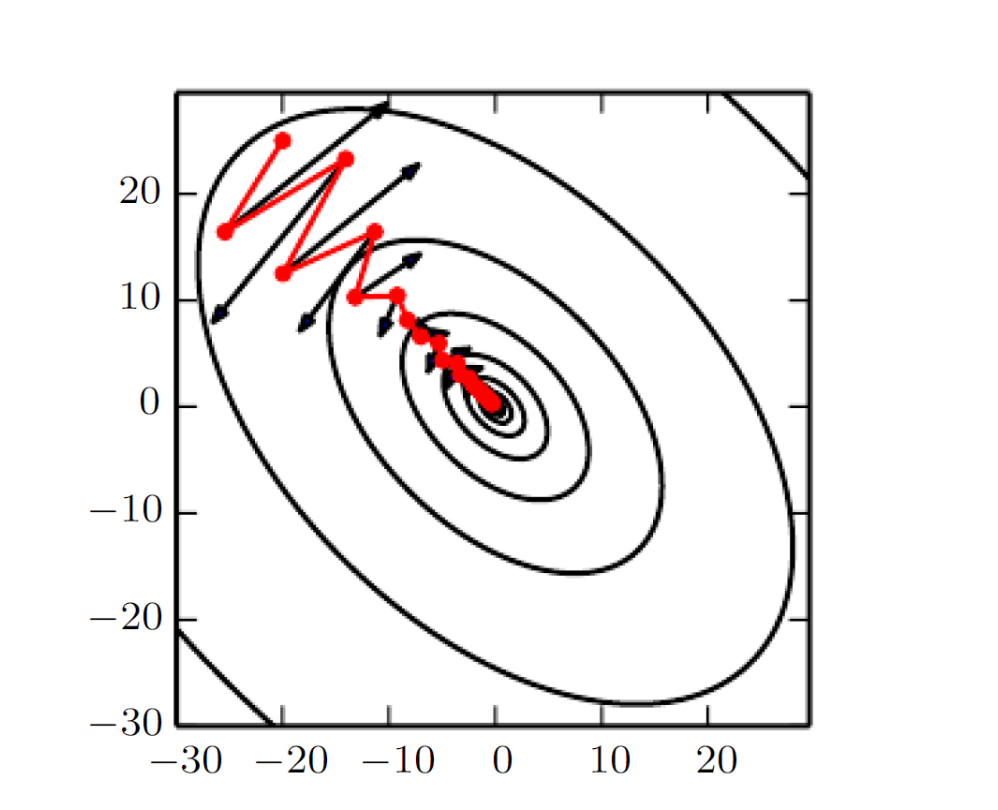

이는 마치 물리 법칙의 가속도와 비슷한 개념으로 이해할 수 있으며, 지수적으로 감소하도록 이동 평균을 누적하여 과거 그래디언트의 영향력은 줄인다.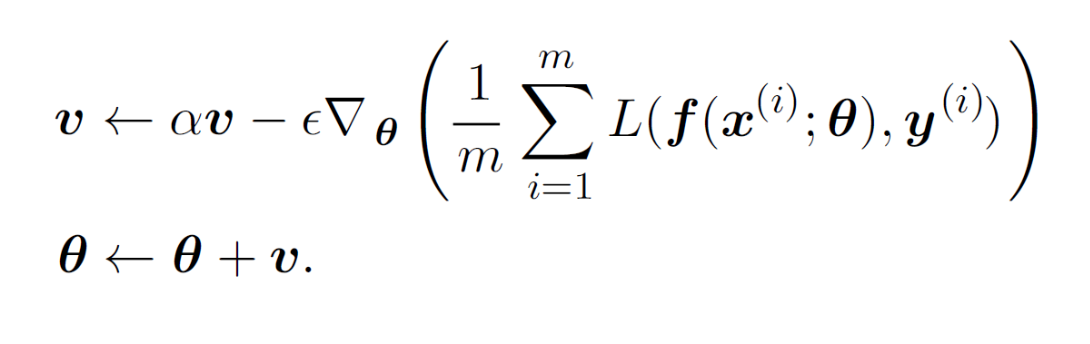

• $\alpha$ : Momentum

• $\theta$ : 가중치(Parameter)

단순 SGD보다 진동을 줄이고, 안정적인 학습(빠르게 수렴)하도록 한다.

AdaGrad

적응형(Adaptive) 방식으로 그래디언트의 학습률을 조정하는 방식이다.

즉, 각 파라미터마다 학습률을 개별적으로 조정하여 그래디언트 변화율이 큰 파라미터는 학습률을 줄이고, 변화율이 큰 파라미터는 학습률을 높인다.

RMSProp

AdaGrad의 단점을 개선하기 위해 과거 그래디언트의 영향력을 줄이는(Smoothing) 방식이다.

Adam

Adaptive(RMSProp) + Momentum

Parameter Initialization Strategies

파라미터 초기화는 시작 지점을 지정하는 것과 같은 의미이다. 좋은 초기 지점을 설정하는 것은 학습이 안정적으로 진행(빠른 수렴, 좋은 일반화)하는 데 필수적이다.

초기값이 너무 크거나 작을 경우, 사라지는 기울기 혹은 폭발하는 기울기 문제가 발생할 수 있다.

최적의 초기값을 미리 아는 것은 매우 어렵기 때문에, 우리는 경험적(Heuristic) 초기화 전략을 사용해야 한다.

파라미터 초기화를 위한 기본적인 아이디어는 다음과 같다.

• Break symmetry(대칭을 깬다) : 초기 파라미터를 대칭적으로 구성할 경우, 각 파라미터들이 함께 움직일 수 있다(동일한 값으로 업데이트).

• Scale of initial weights

  • Small : 정규화에 유리

  • Large : 대칭을 강하게 깰 수 있고, 역전파 중 신호 손실을 방지

  • Too large : 가중치 폭발 문제 발생 가능

결론적으로, 파라미터는 다음과 같이 초기화 해야 한다.

• 엔트로피가 높은 분포로부터 무작위로 초기 가중치 생성(Gaussian or Uniform)

• Heuristic (과거 경험에 기반한 규칙 적용)

• 정규화된 초기화 적용 (Xavier 초기화)

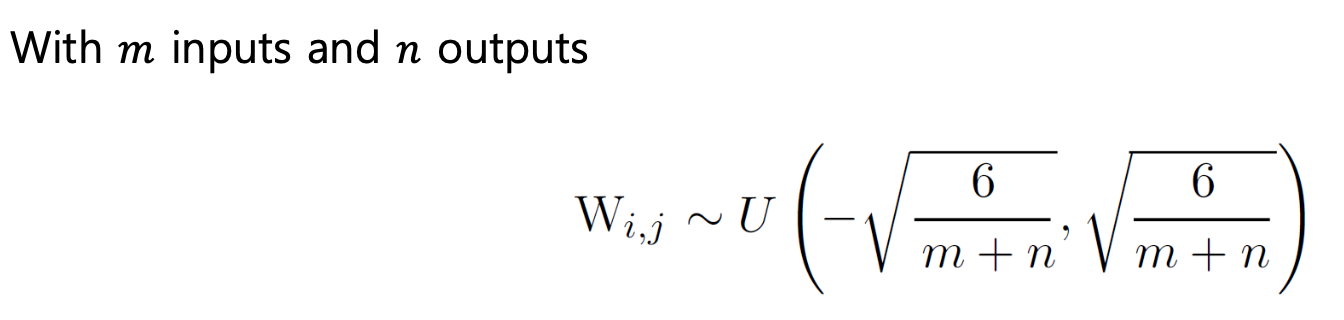
Optimization Strategies

DNN에서 Internal Covariate Shift(내부 공변량 변화)라는 문제가 존재한다.

DNN은 여러 계층이 쌓여있는 구조로, 한 층의 출력은 다음 층의 입력이 된다. 학습이 진행됨에 따라 각 층의 파라미터는 업데이트 되므로, 다음 층이 받게 되는 입력 분포는 계속해서 변한다.

입력 분포가 가변적이라는 것은 학습이 불안정해지며 수렴 속도가 느려짐을 의미한다.

이를 해결하기 위해 Batch Normalization(배치 정규화)라는 기법이 사용되며, 이는 각 층의 출력값을 평균이 0, 분산이 1인 분포로 정규화하는 것이다.

배치 정규화 진행 과정은 다음과 같다.

1) 선형 변환

$Z = XW$

• $X$ : 입력 벡터

• $W$ : 파라미터 행렬

2) 평균 정규화

$\tilde{Z} = Z - \frac{1}{m}\sum_{i=1}^m{z_{i.:}}$

• $m$ : 미니배치 크기

• $z_{i.:}$ : $i$번 째 샘플의 은닉 출력

3) 분산 정규화

$\hat{Z} = \frac{\tilde{Z}}{\sqrt{\epsilon+\frac{1}{m}\sum_{i=1}^m{\tilde{z_{i.:}}^2}}}$

• $\epsilon$ : 분모가 0이 되는 것을 방지하는 작은 수

4) 출력 정규화

$H = max(0, \gamma \hat{Z} + \beta)$

배치 정규화를 통해 얻을 수 있는 이점은 다음과 같다.

• 학습 안정성 보장

• Internal Covariate Shift 제거

• 정규화 효과 제공