[Deep Learning] Generative Model - Autoencoder

이한량·2025년 6월 4일

Deep Learning

목록 보기

8/10

일반적인 분류 모델은 입력 데이터 $x$ 로부터 정답 $y$ 를 예측하는 데 집중한다. 즉, 클래스를 구분하는 경계를 찾는 것을 학습 목표로 한다.

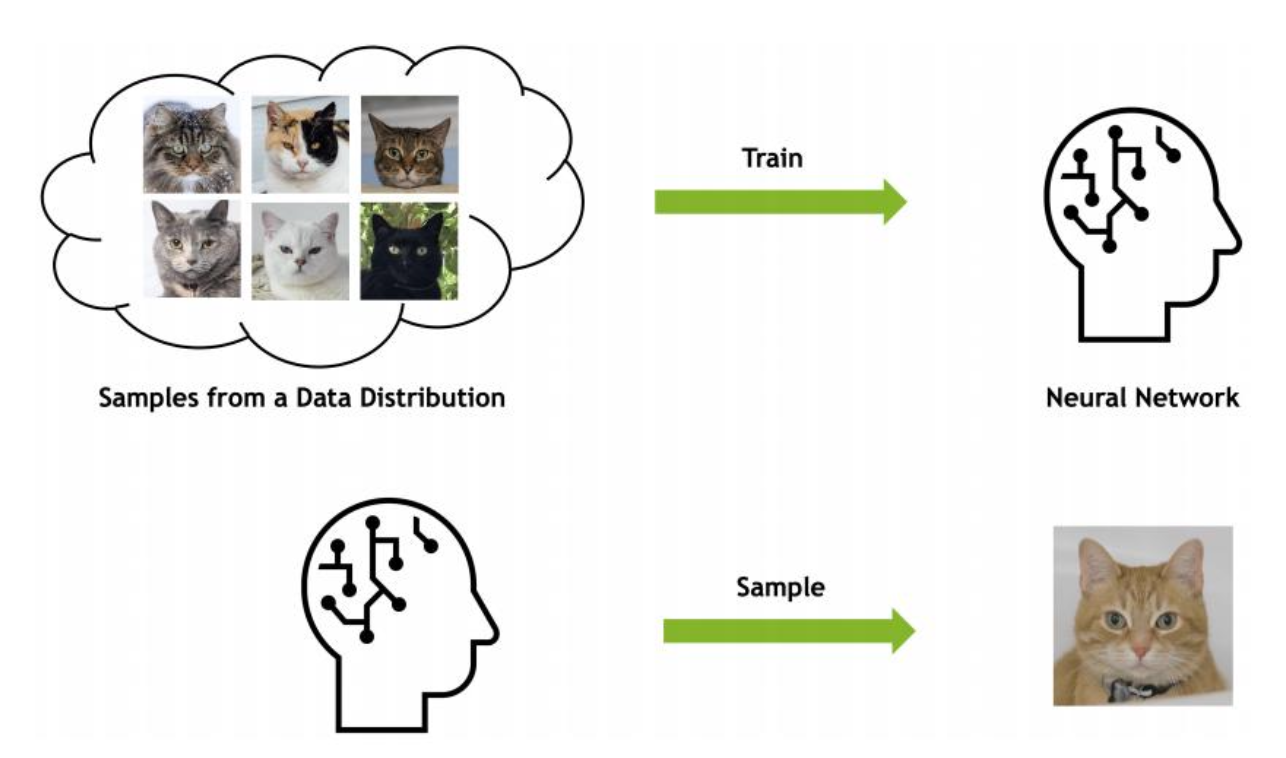
이와 달리 생성형 모델은 실제 데이터의 분포 자체를 학습하는 것을 목표로 하며, 정답 $y$ 에 대한 입력 분포 $x$ 를 추정하고자 한다.

즉, 생성형 모델은 실제 데이터의 분포를 학습하여 그와 유사한 데이터의 분포를 생성하는 것을 목표로 하는 모델이다.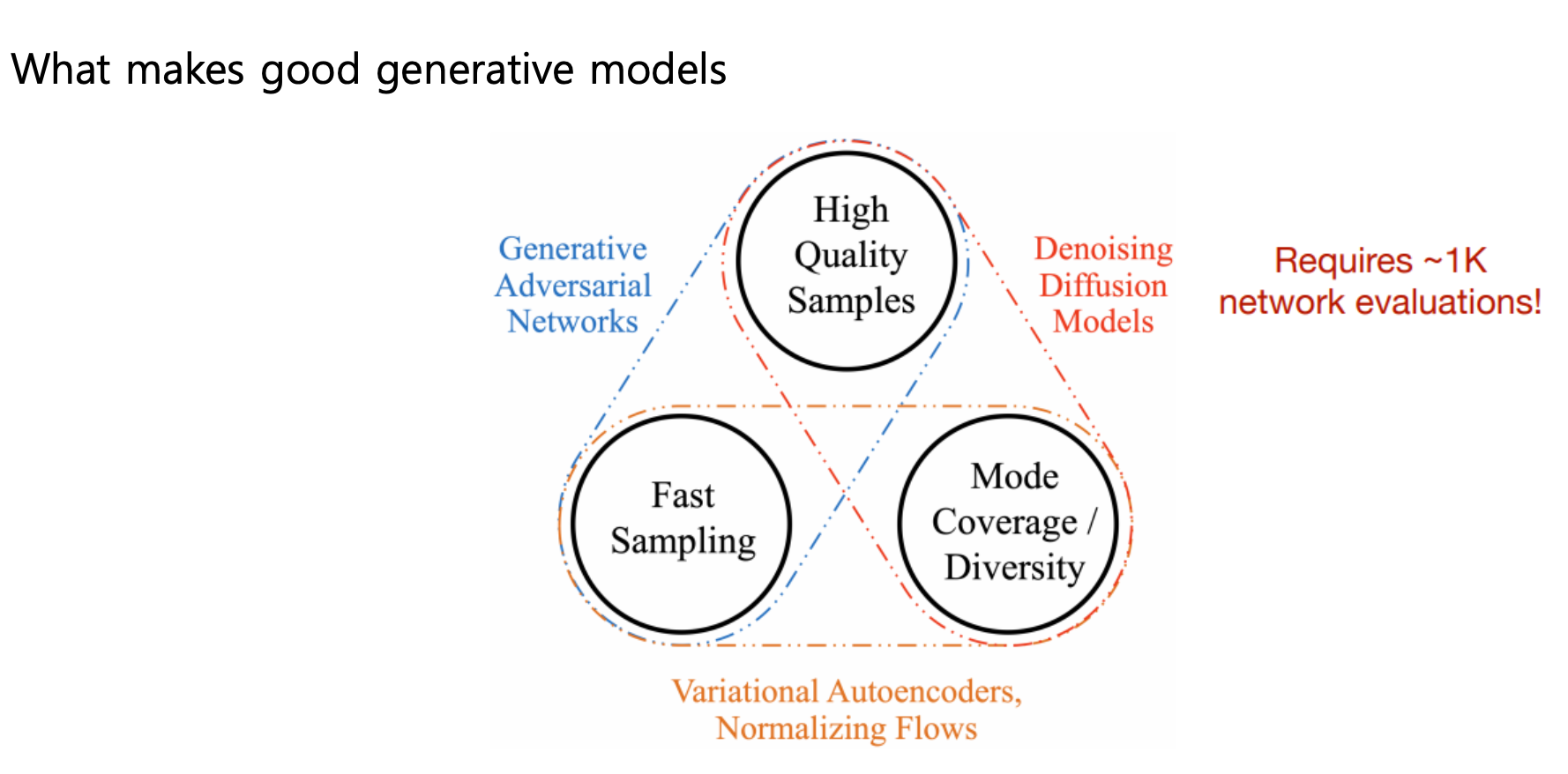

Autoencoder

오토인코더는 엄밀한 의미에서 생성형 모델은 아니지만, VAE를 이해하기 위해 선행적으로 이해가 필요한 아키텍처이다.

오토인코더는 입력 데이터의 특징을 추출 및 축약하는 인코더와 압축된 벡터를 복원하여 원본과 비슷하게 만들어내는 디코더로 이루어진 네트워크이다.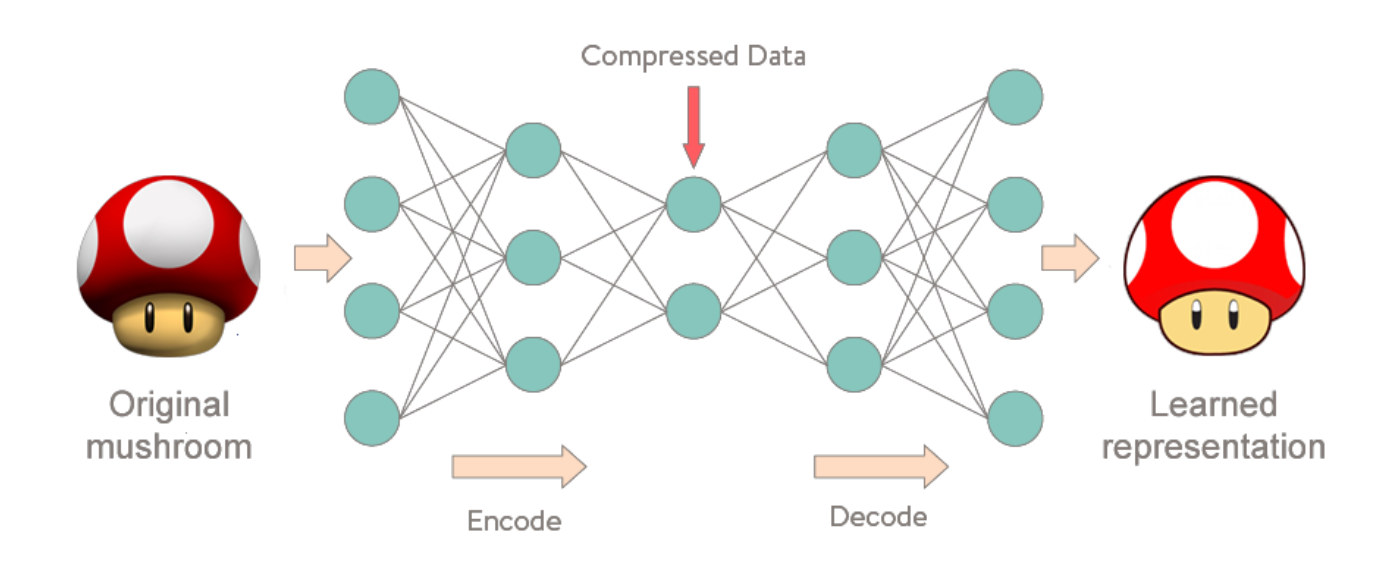

Feature extraction

인코더가 입력 이미지를 압축하여 잠재 변수를 구성하는 과정을 Feature extraction이라고 하며, 이 잠재 변수를 디코더가 복원하는 과정에서 오토인코더의 학습이 이루어진다.

오토인코더의 학습의 결과로 인코더는 더 좋은 특징을 추출할 수 있게 되며, 디코더는 잠재 변수를 기반으로 원본 이미지와 가까운 이미지를 생성할 수 있게 된다.

Novelty detection

오토 인코더는 입력 이미지와 출력 이미지 간 데이터 분포의 차이로 복원 오차를 정의한다.

l(f(x)) = \frac{1}{2}\sum_k(\hat{x_k}-x_k)^2

만약 복원 오차가 크다면, 이전에 학습했던 데이터와 다른 새로운 데이터가 입력으로 들어왔다는 것을 감지할 수 있다. 이를 Novelty detection(이상치 탐지)이라고 한다.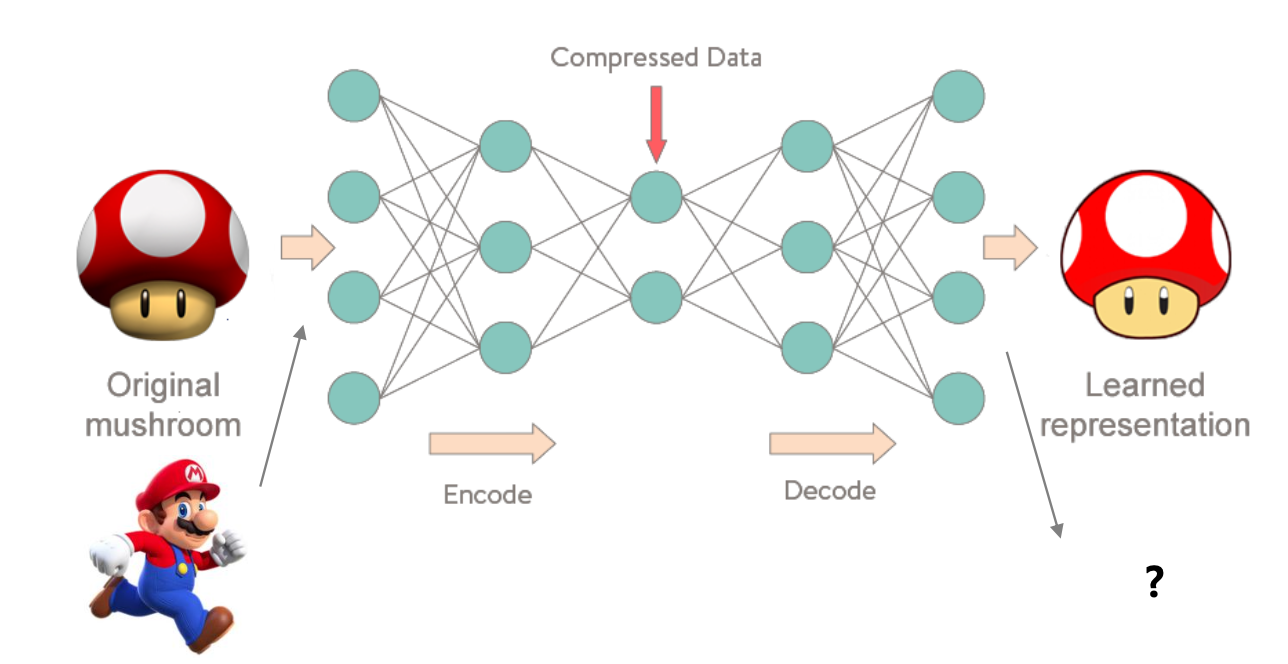

Deep autoencoder

기본적인 오토인코더 아키텍처는 선형 패턴만 추출할 수 있는 한계점이 존재한다.

MLP와 동일한 원리로, 비선형 패턴을 효과적으로 추출하기 위해 더 깊은 층을 쌓은 오토인코더 아키텍처가 제시되었다.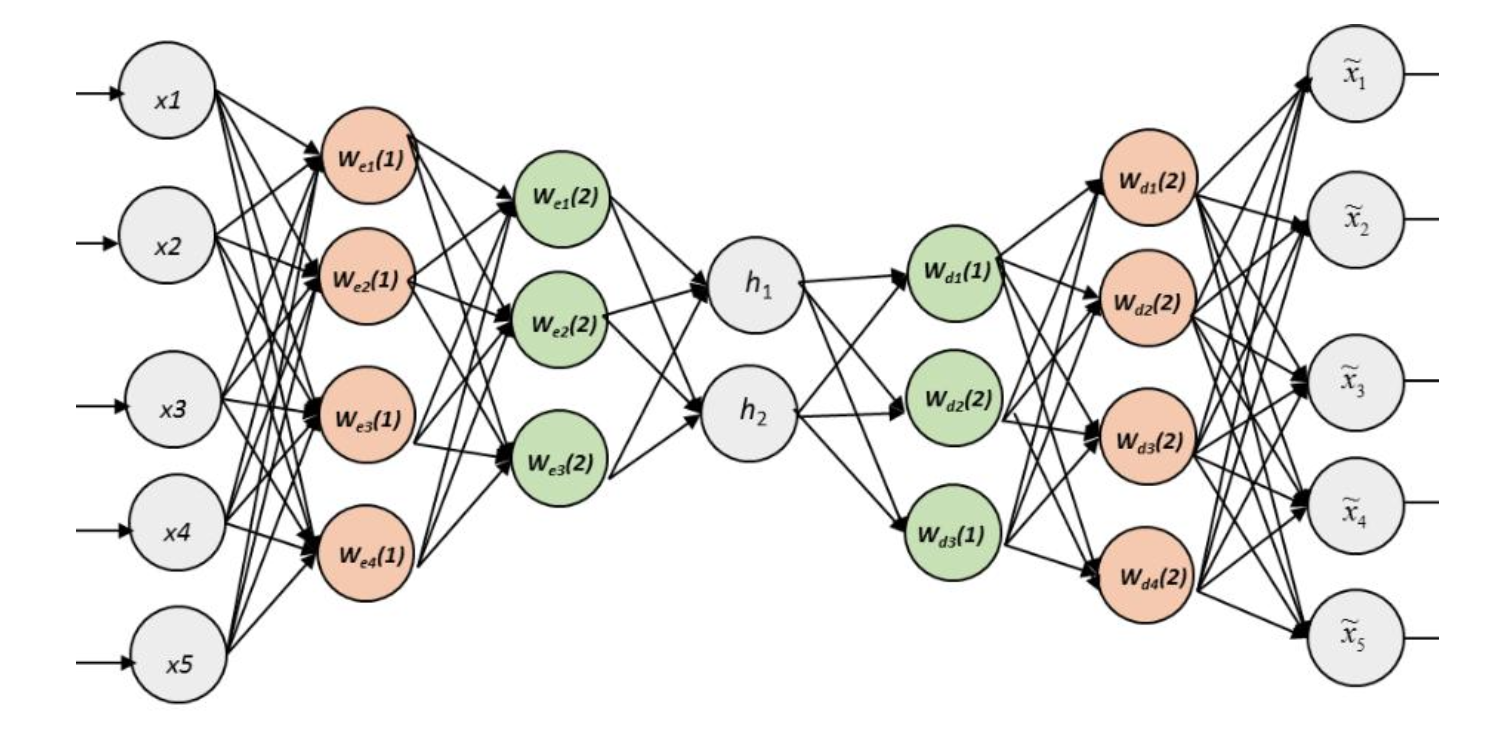

여러가지 변형이 가해진 Deep autoencoder 아키텍처들이 존재한다.

인코더-디코더가 완벽하게 대칭(Symmetric) 구조를 이루도록 하여 인코더의 가중치를 디코더와 공유하도록 하는 구조이다.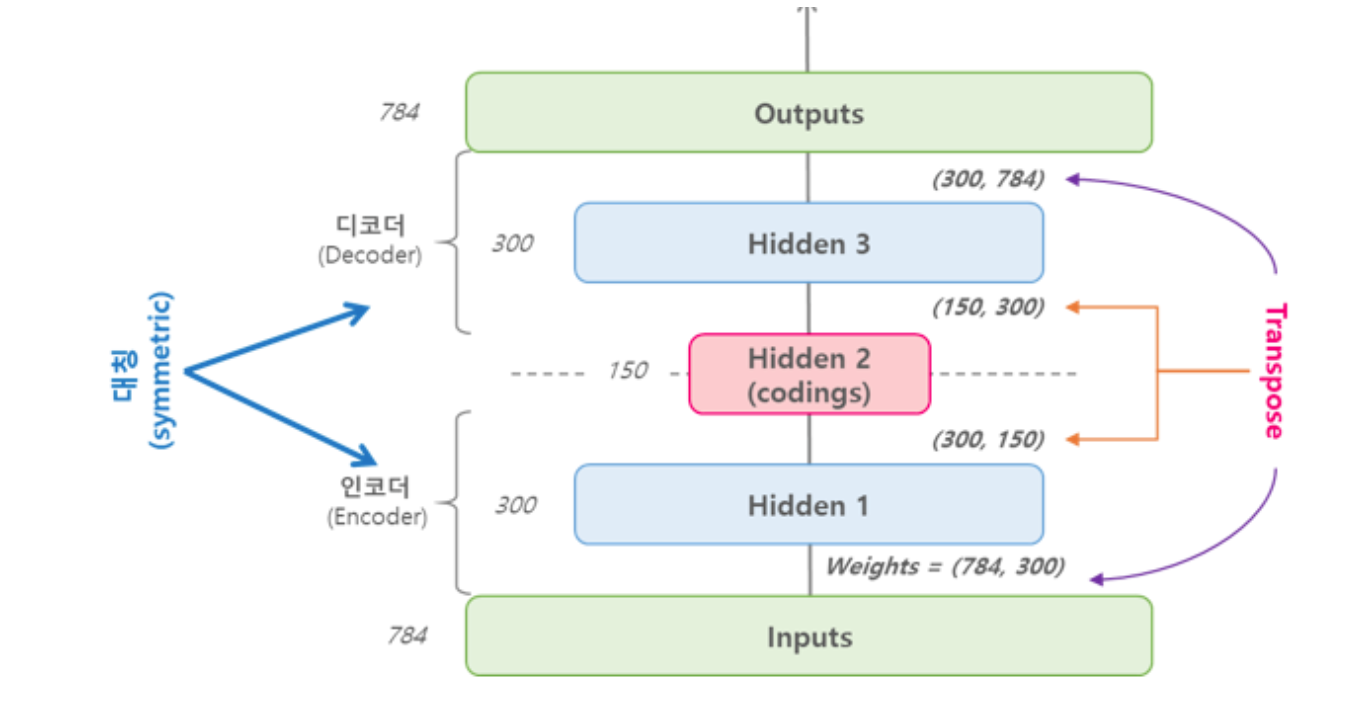

이는 네트워크 파라미터의 수가 절반으로 줄어들기 때문에 학습의 수렴 속도가 빨라지며, 과적합을 방지하는 효과가 있다.

Sequential learning

딥 오토인코더를 한번에 학습시키지 않고, 단계별로 순차적으로 학습시키는 방법이다.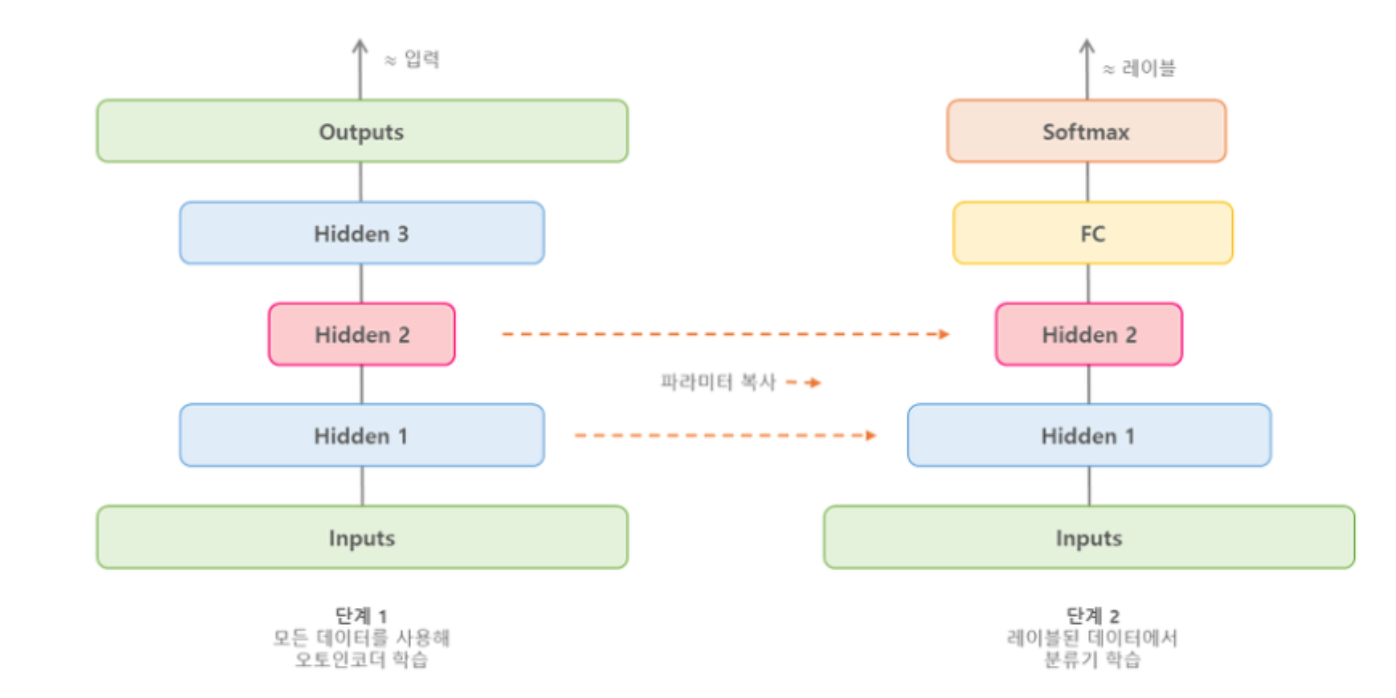

Denoising autoencoder (DAE)

DAE는 기본적인 구조는 오토인코더와 동일하지만, 입력 이미지에 노이즈를 추가하여 인코더에 전달한다.

입력 이미지에 노이즈를 추가하는 것은 일종의 정규화 역할을 하게 된다. 따라서 모델은 더 좋은 특징을 추출할 수 있게 되며, 노이즈에 대해서도 강건하게(Robust) 동작할 수 있는 모델이 된다.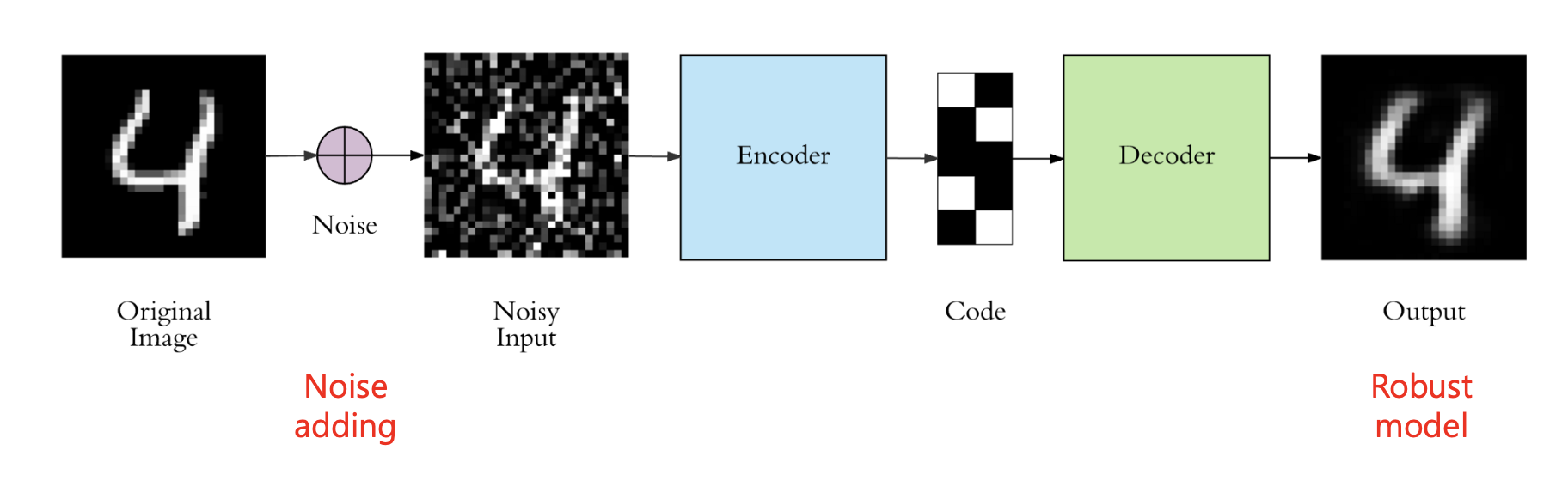

손실 함수는 복원된 출력 $\tilde{x}$ 와 원본 입력 $x$ 사이의 차이를 계산하는 것으로 정의된다.

L(x, g(f(\tilde{x}))) \\ \tilde{x} = x + noise \\

f : 인코더 \\ g : 디코더

Convolutional autoencoder (CAE)

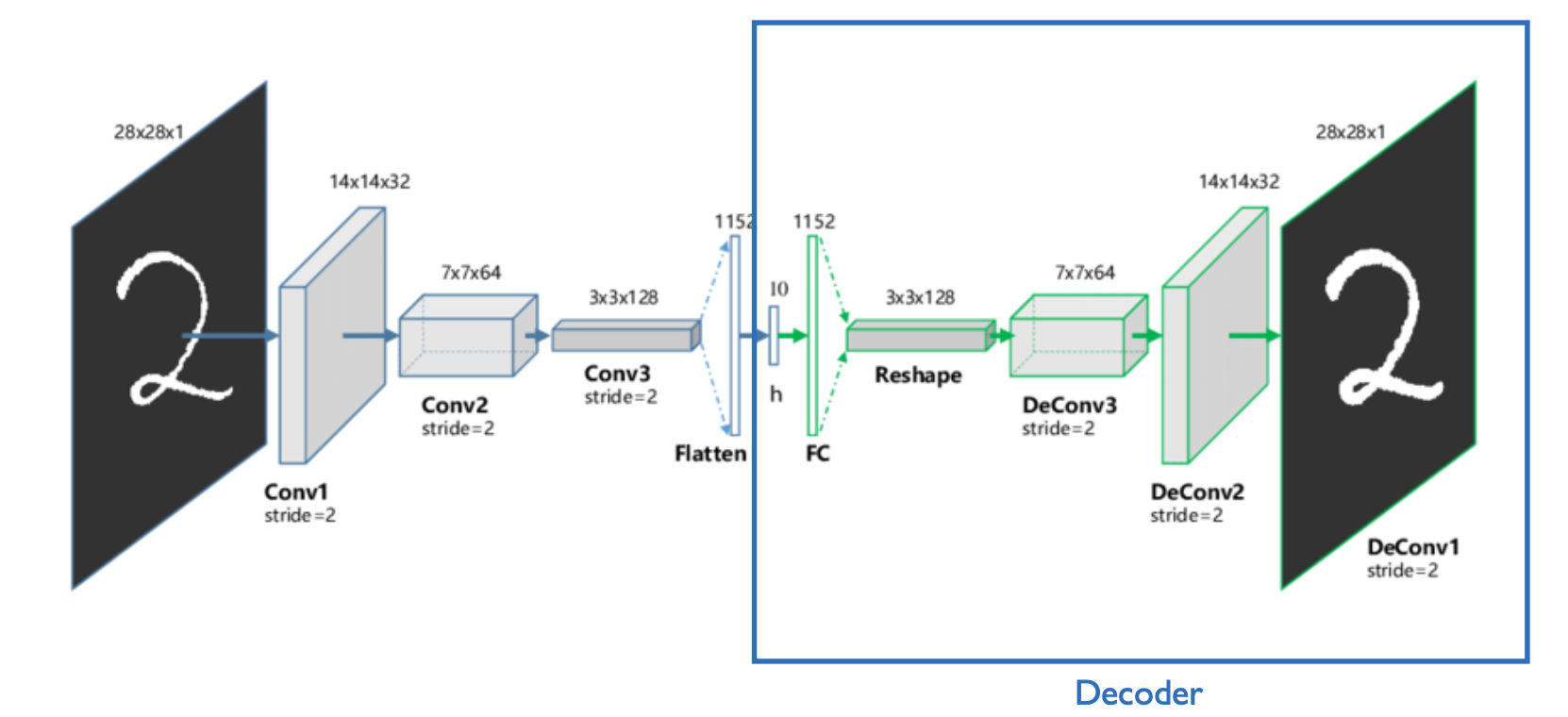
CAE는 기본적으로 오토인코더와 동일한 원리이지만, 인코딩과 디코딩과정에서 CNN 네트워크를 거치도록 설계된 아키텍처이다.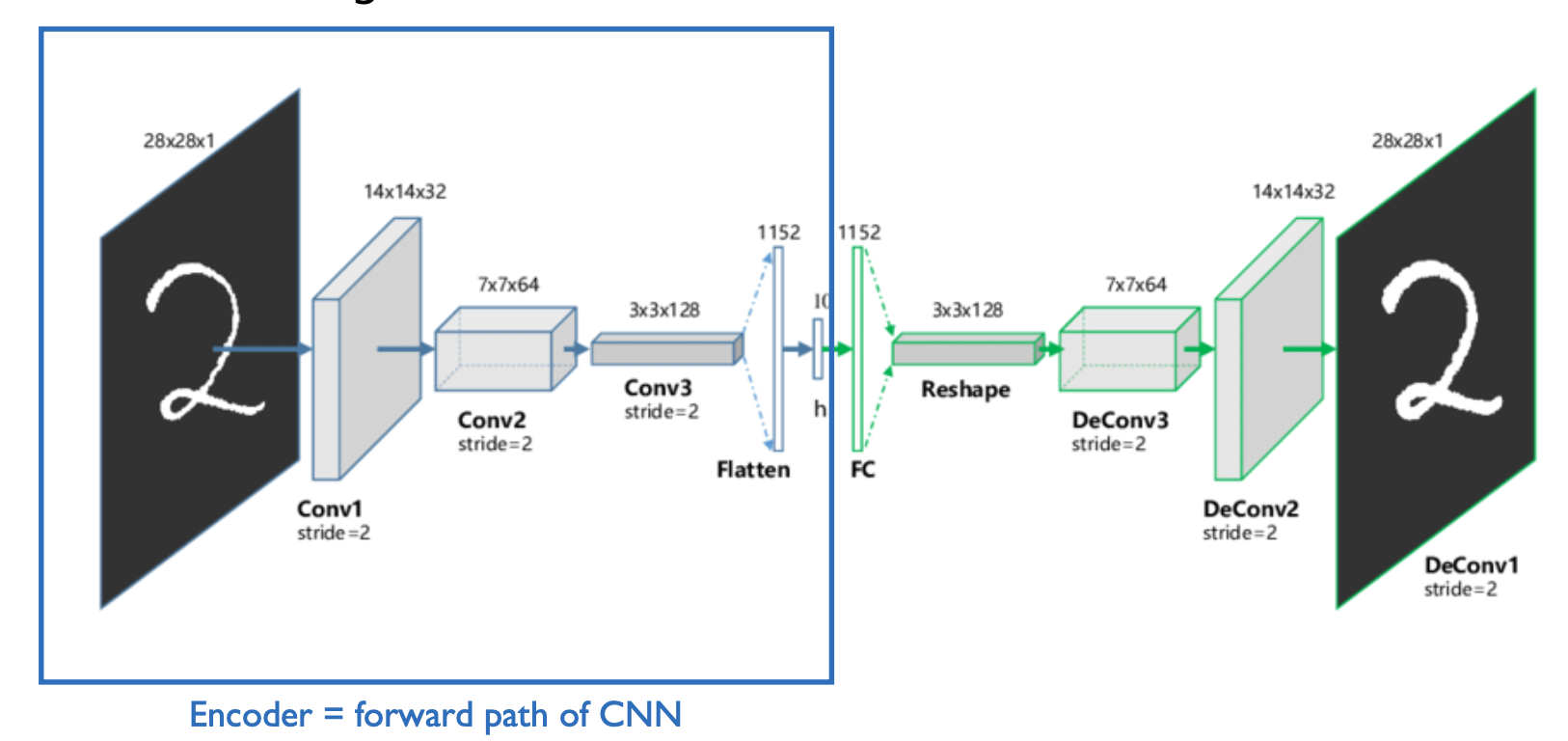

Unpooling

CAE는 입력 이미지를 인코딩하는 과정에서 Pooling 연산이 활용될 수 있다(CNN 이니까). 이때 Pooling 과정에서 대표값의 위치(인덱스)를 저장하며, 디코딩 과정에서 해당 인덱스를 통해 대표값이 원래 위치로 복원되도록 한다.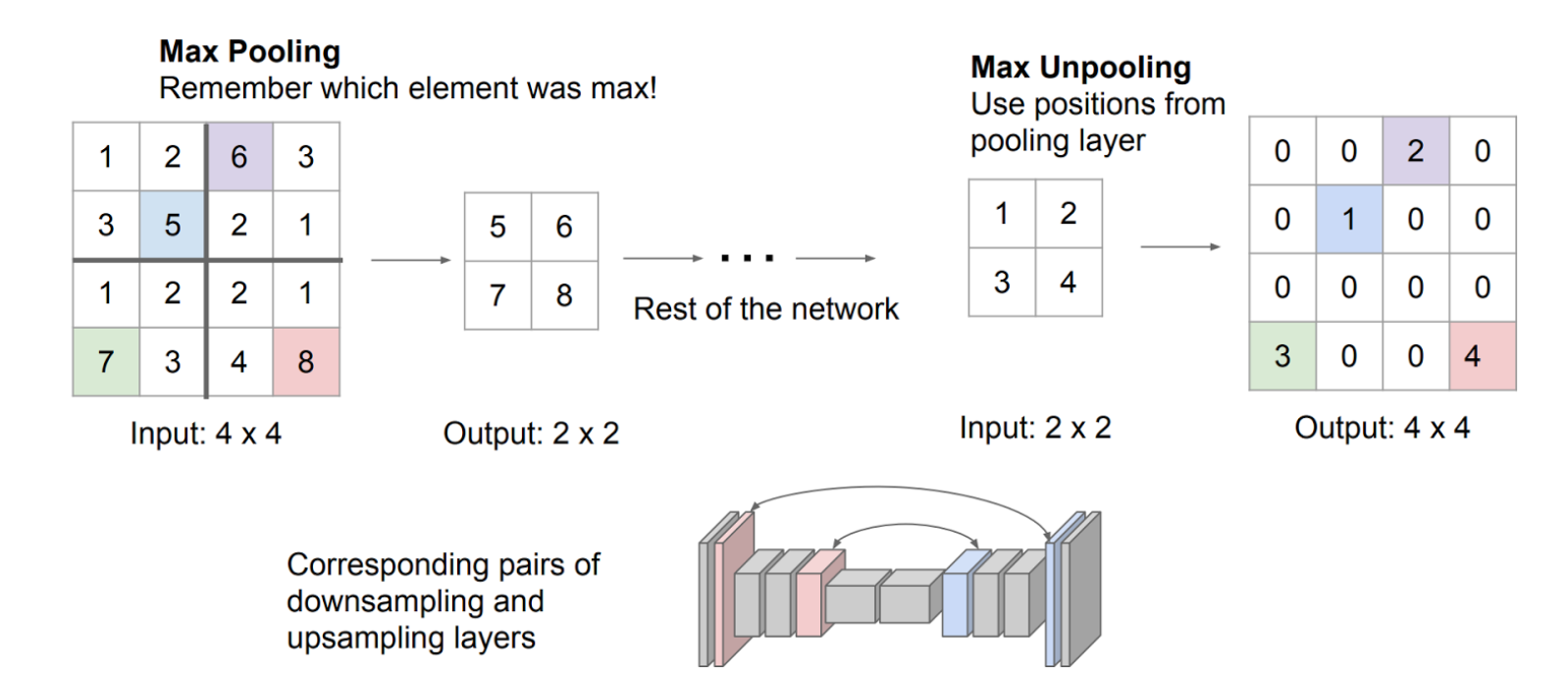

이를 Unpooling이라고 하며, 이는 원본 이미지의 정보와 최대한 유사하게 복원하도록 돕는다.

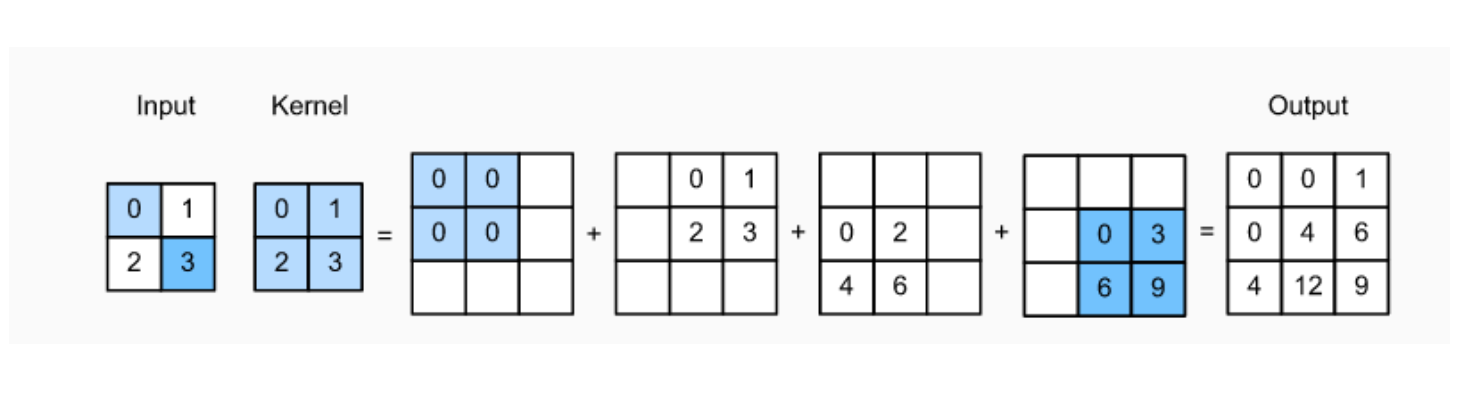
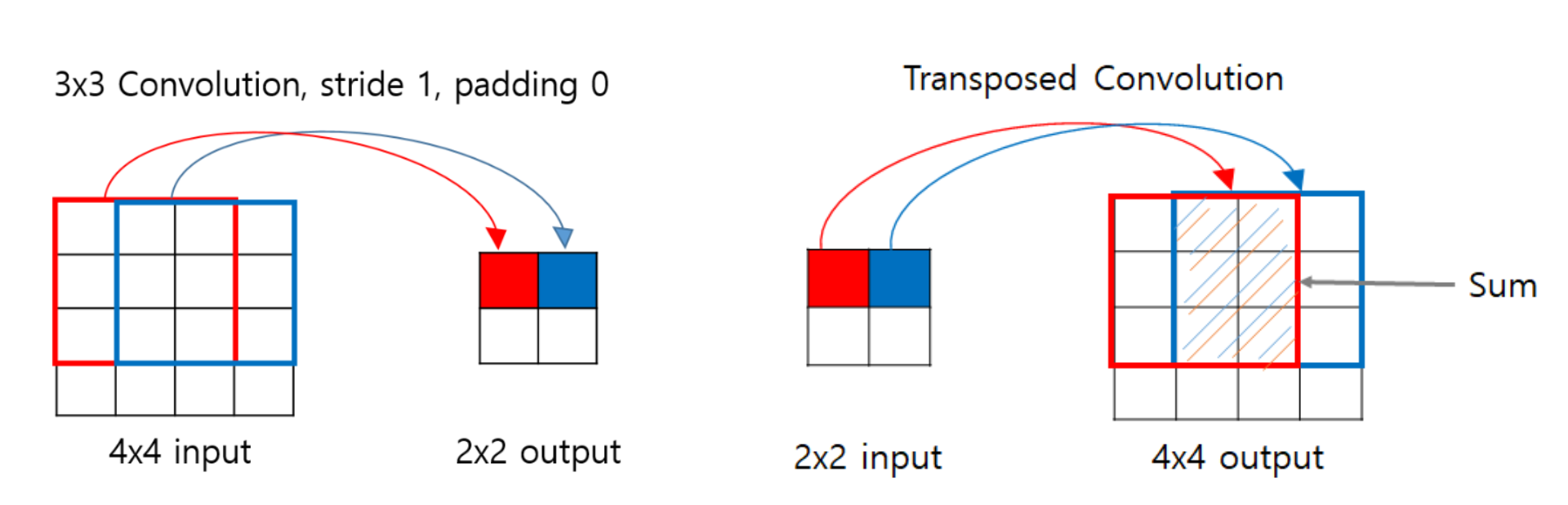
Transpose convolution

이미지에 합성곱 연산을 진행할 경우, 이미지의 크기가 줄어들게 된다. Transpose convolution은 합성곱의 반대 연산으로, 이미지의 크기를 복원하기 위한 연산이다.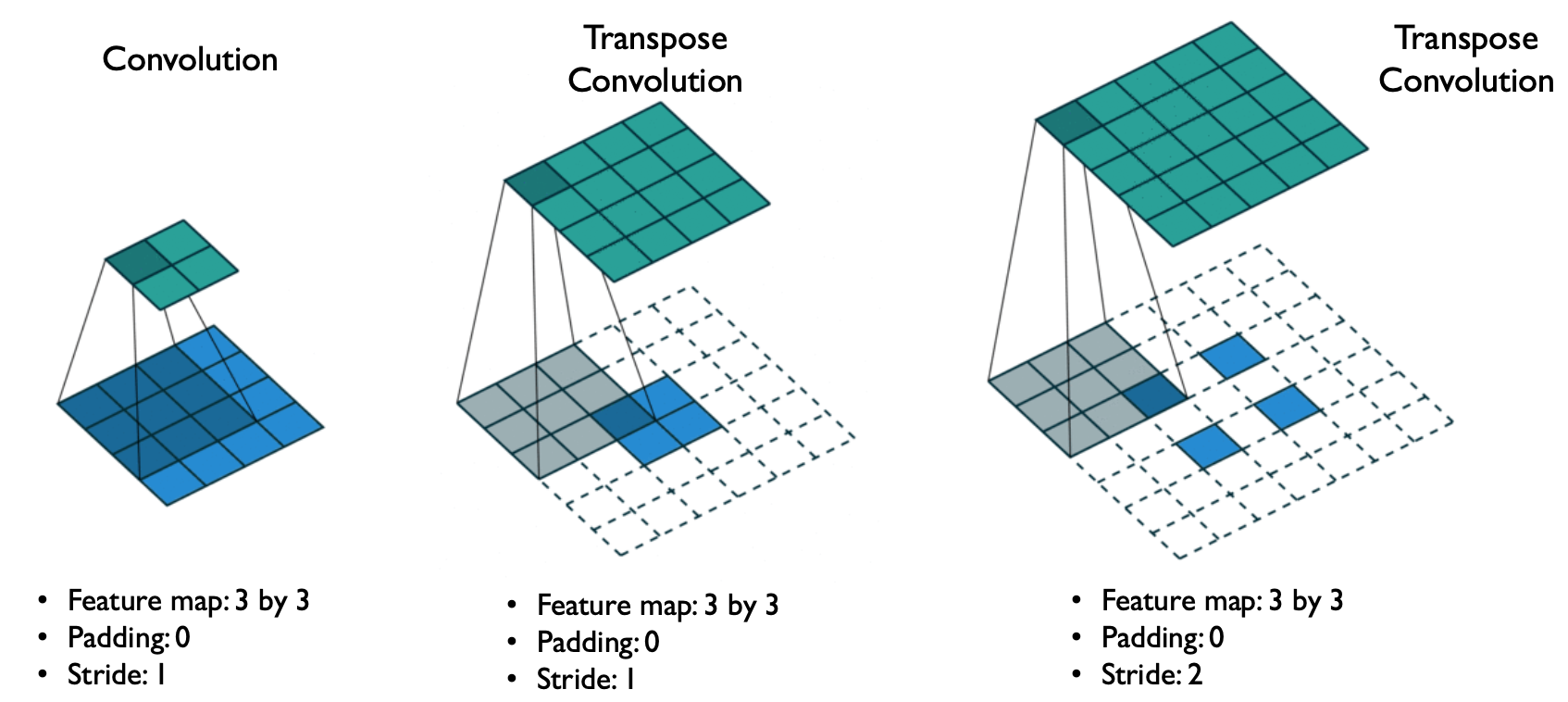

Variational autoencoder(VAE)

이제 진정한 의미의 생성형 모델인 확률형 오토인코더(VAE)에 대해 살펴보자.

오토인코더의 인코더는 입력 데이터 $x$ 가 주어졌을 때, 이를 잘 표현할 수 있는 잠재 변수 $z$ 로 변환하였다.

VAE의 인코더는 이와 달리 입력 데이터 $x$ 가 주어졌을 때, $x$ 와 연관되어 있는 잠재 변수 $z$ 에 대한 확률 분포 $p(z|x)$ 를 근사하고자 하는 것을 목표로 한다. 즉, 인코딩의 결과는 연속적인 잠재 변수 $z$ 의 확률 분포가 된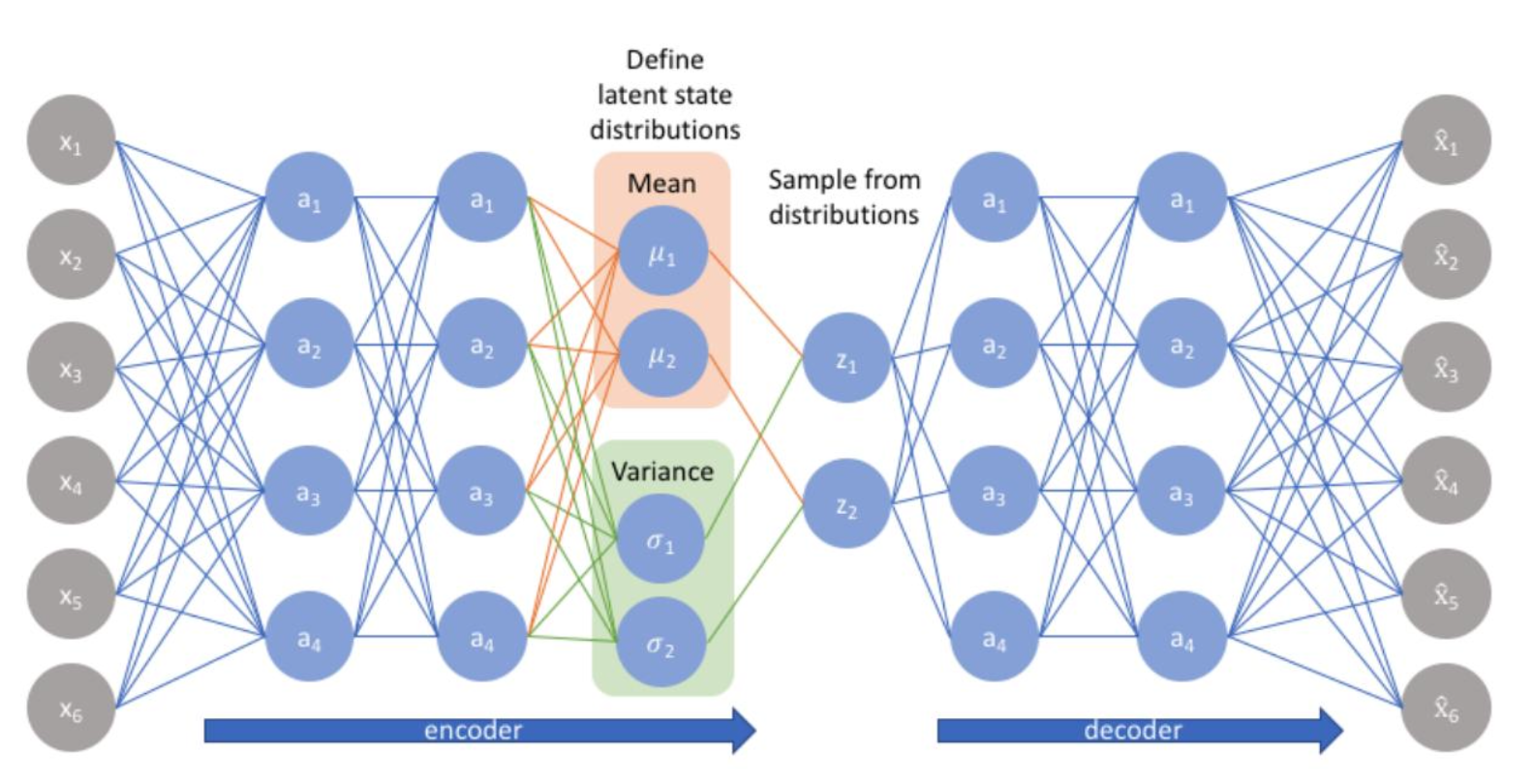다.

다시 말해 VAE는 입력 데이터 $x$ 가 잠재 공간 $z$ 와 연결되었다고 가정하고, $x$ 의 특징을 추출하여 잠재 공간 $z$ 에 투영한다. 따라서 더 간단한 분포인 $q_{\phi}(z|x)$ 를 $p(z|x)$ 에 근사하는 과정으로 이해할 수 있다.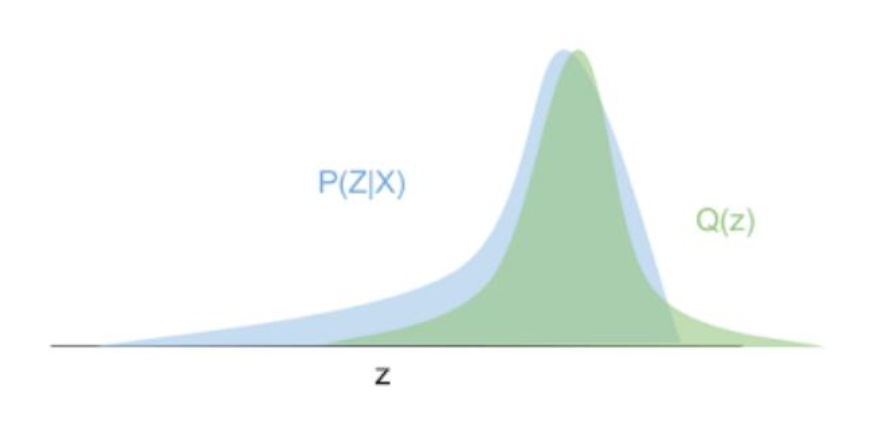

Encoder

확률 분포의 모양은 평균 $(\mu)$ 과 표준 편차 $(\sigma)$ 에 의해 결정된다.

따라서 VAE 인코더의 목표는 입력 $x$ 에 대한 잠재 변수 $z$ 의 분포인 $q(z|x)$ 를 잘 표현할 수 있는 $(\mu, \sigma)$ 를 찾아내는 것과 같다.

이때, 일반적으로 $q$ 의 분포를 정규 분포(가우시안 분포)로 가정한다.

Decoder

디코더는 인코더가 학습한 잠재 변수의 확률 분포(가우시안 분포)로부터 특정 잠재 변수 $z$ 를 샘플링하며, 이를 복원하는 과정을 거친다.

즉, 확률 분포 $p_{\theta}(x|z)$ 에서 데이터를 복원하는 과정이다.

Loss function

Reconstruction Loss

재구성 손실(Reconstruction Loss)은 다음과 같이 정의되며, 샘플링한 $z$ 로부터 데이터 $x^{(i)}$ 가 얼마나 잘 복원되었는지 나타낸다.

\mathbb{E}_z \left[ \log p_{\theta}(x^{(i)}|z) \right]

따라서 VAE의 디코더는 재구성 손실을 최소화하는 것을 목표로 한다.

KL-Divergence

KL 발산은 다음과 같이 정의되며, 인코더가 근사한 분포 $q(z|x)$ 와 사전 분포 $p_{\theta}(z)$ 간 차이로 나타낸다.

D_{KL} \left( q_{\phi}(z|x^{(i)}) \,||\, p_{\theta}(z) \right)

따라서 VAE의 인코더는 KL-Divergence를 최소화하는 것을 목표로 학습된다.

ELBO

ELBO는 다음과 같이 정의된다.

\text{ELBO} = Reconstruction Loss - KL-Divergence

\underbrace{ \mathbb{E}_z \left[ \log p_{\theta}(x^{(i)}|z) \right] - D_{KL} \left( q_{\phi}(z|x^{(i)}) \,||\, p_{\theta}(z) \right) }_{\mathcal{L}(x^{(i)}, \theta, \phi)}

x^{(i)} : 입력 데이터 \\ z : 잠재 변수 \\ p_{\theta} :디코더 \\ q_{\phi} : 인코더

VAE는 ELBO를 최대화하는 것을 목표로 하며, 일반적으로 Loss 함수는 $-ELBO$ 의 형태로 활용된다.

이한량

한량 극복 프로젝트

이전 포스트

[Deep Learning] Sequence Model - Transformer

다음 포스트

[Deep Learning] Generative Model - Autoencoder

Deep Learning