
내적(Dot product)
두 벡터 a,b가 있다고했을 때 두 벡터의 내적은 아래와 같이 길이와 두 벡터 사이의 각도로 표현이된다.
|a| x |b| x cosθ
위 식으로부터 두 벡터가 같은 방향을 가질 때는 코사인이 양의 값을 가지므로 결과값은 양수가되고 반대 방향을 가질 때는 같은이유로 결과가 음수가되고 직교하면 결과는 0이된다는 것을 알수있다 즉 내적은 두 벡터가 얼마나 유사한지 측정하는 기준이 될 수 있다.
퍼셉트론(perceptron)
- 신경망에서 사용하는 분류기 모델
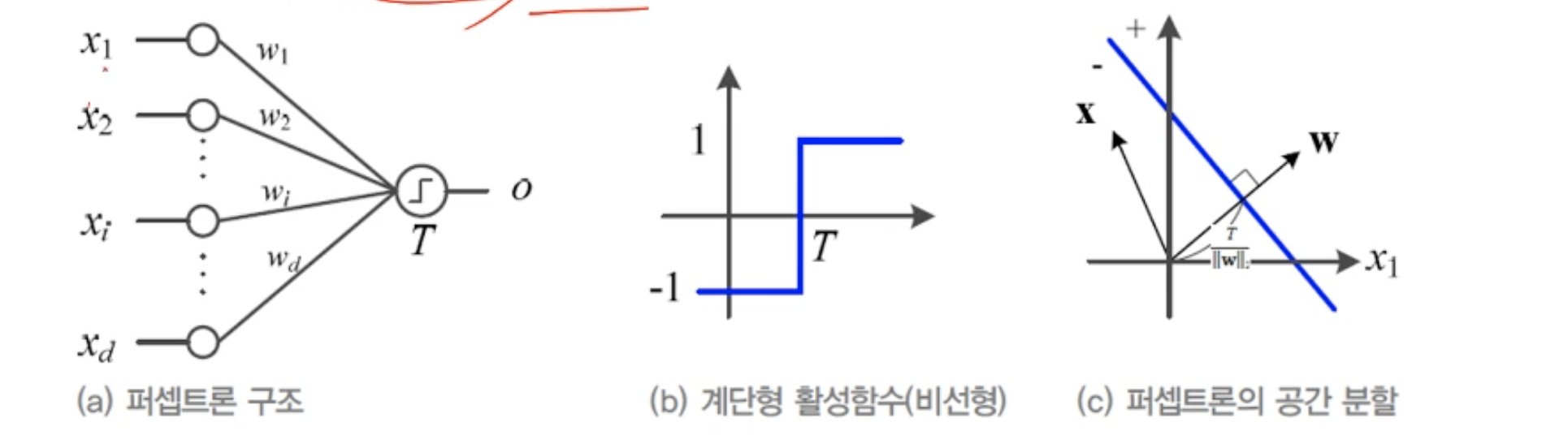
퍼셉트론은 입력에 가중치를 곱해서 더한값, 입력과 가중치(W)들을 내적을 수행한 결과를 어떤 기준 보다 높으면 출력하고 아니면 출력하지않도록 동작한다. 이 때 기준이 되는 함수를 활성함수(activation function)라고하며 이를 공간상에서 표현했을 때 입력벡터 X와 가중치 벡터 W의내적이 어떤 기준을 넘어가느냐 마냐로 볼 수 있다. 즉 X와 W의 유사도가 높다면 기준을 넘어갈 것이고 유사도가 적다면 기준에 미치지 못 할 것이다. 참고로 활성화 함수는 sigmoid, Relu, tanh 등 다양한데 아래는 가장 기본적인 step function을 예로한 것이다.
놈(norm), 프로베니우스 놈(Frobenius norm)
- 놈 : 벡터의 크기, 길이
놈은 차수에따라 1차부터 차수가 무한대인 최대 놈(max)까지 존재하며 기하학 적으로 몇가지만 보면 아래와같고 그래프는 차수별로 모두 크기가 1인 지점을 나타낸다.![]
놈이 사용되는 부분은 예측데이터와 실제데이터의 차이를 표현하는 손실함수에서 규제항 부분이다.
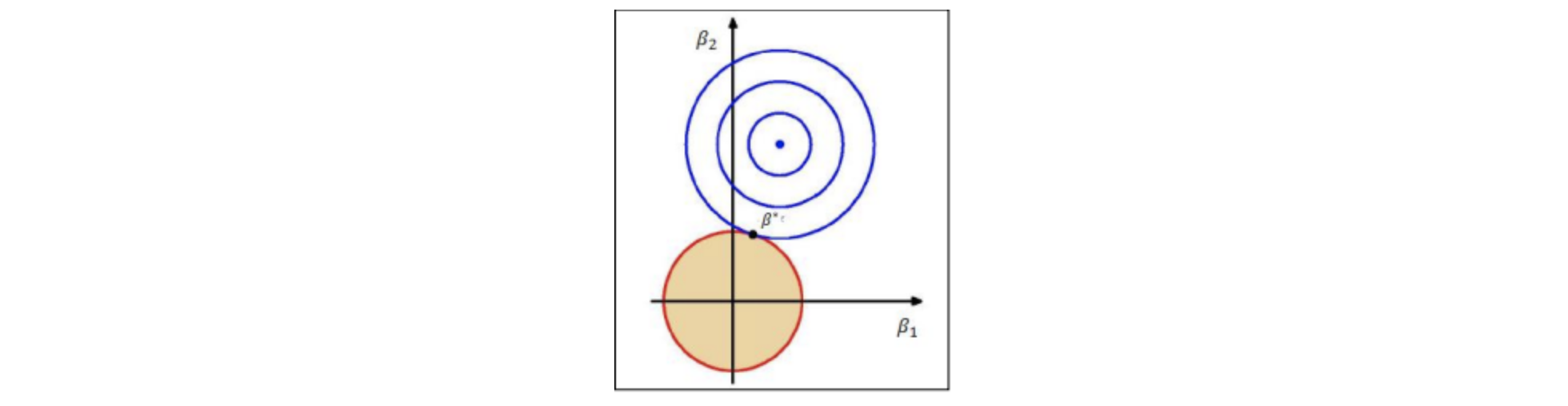
아래의 파란색의 동심원들은 손실함수에서 손실이 같은부분을 나타내며 원의 지름이 클수록 손실이 크다고 보면된다. 이 때 당연히 파란 동심원이 거의 점에 가까울 때 예측이 가장 잘 되었고 최적의 파라미터를 가졌다고 볼 수 있으나 그렇기 때문에 모든 파라미터가 발현되어 과대적합(overfitting)문제가 발생할 수 있다. 따라서 빨간색 원으로 표현되는 L2 norm이 제약조건, 규제부분이되어 이 파라미터의 발현을 억제함으로써 과대적합을 개선할 수 있다.
- 프로베니우스 놈 : 행렬의 크기

행렬식(determinant)
- 역행렬의 존재유무를 알 수 있는 값 : 0이면 역행렬이 없음
- 기하학적 의미는 주어진 행렬의 곱에의한 공간의 확장 또는 축소의 해석이다.
즉 행렬 A의 행렬식이 아래와 같다고하면,
det(A) = 0 : 하나의 차원을 따라 축소되어 부피를 잃게 됨
det(A) = 1 : 부피 유지한 변환, 방향이 보존 됨
det(A) = -1 : 부피는 유지, 방향은 보존 안됨
det(A) = 5 : 5배 부피가 확장되며 방향은 보존
