Gaussian Elimination (row reduction/echelon form)

nonzero row / nonzero column

: row 또는 column에 한 개 이상의 0이 아닌 entry가 있을때, nonzero row / nonzero column이다.
밑의 그림에서처럼 모두 0인 row 또는 column은 해당되지않는다.

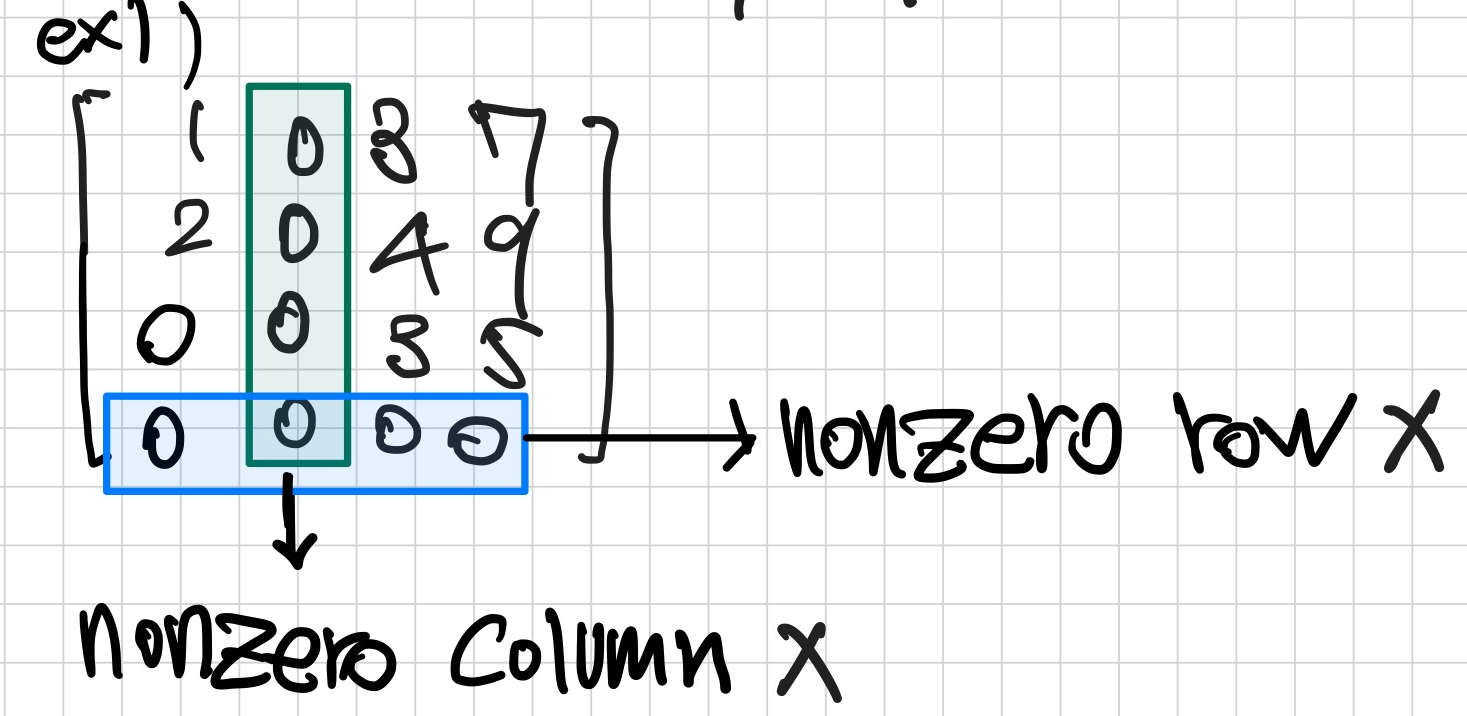
leading entry / leading coefficient

ex1 행렬에서 leading entry 또는 leading coefficient는

• row1 : 1
• row2 : 2
• row3 : 3

Row Echelon Form

1) 모두 0인 행은 마지막 행에 있다.
2) 0이 아닌 entry가 행에서 첫 번째에 있다.
3) 모든 행의 leading entry는 그 위의 행 leading entry의 오른쪽에 위치한다.

Reduced Row Echelon Form

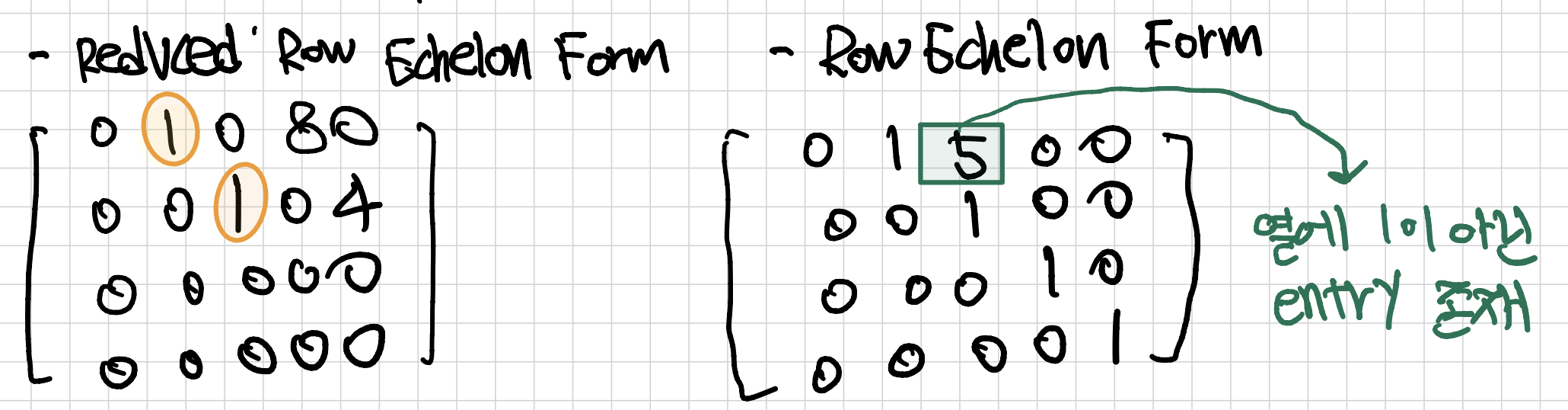
• Echelon Form에서 leading entry가 1인 열에 나머지 entry는 모두 0이면 reduced row echelon form이다.
• Pivot Position : reduced row echelon form에서 leading entry

Theorem. Uniqueness of the Reduced Echelon Form

각 matrix의 reduced echelon matrix는 유일한 형태이다.

augmented matrix → row echelon form

: Gauss elimination (가우스 소거법)

augmented matrix → reduced row echelon form

: Gauss-Jordan elimination (가우스-조단 소거법)

Row Reduction algorithm

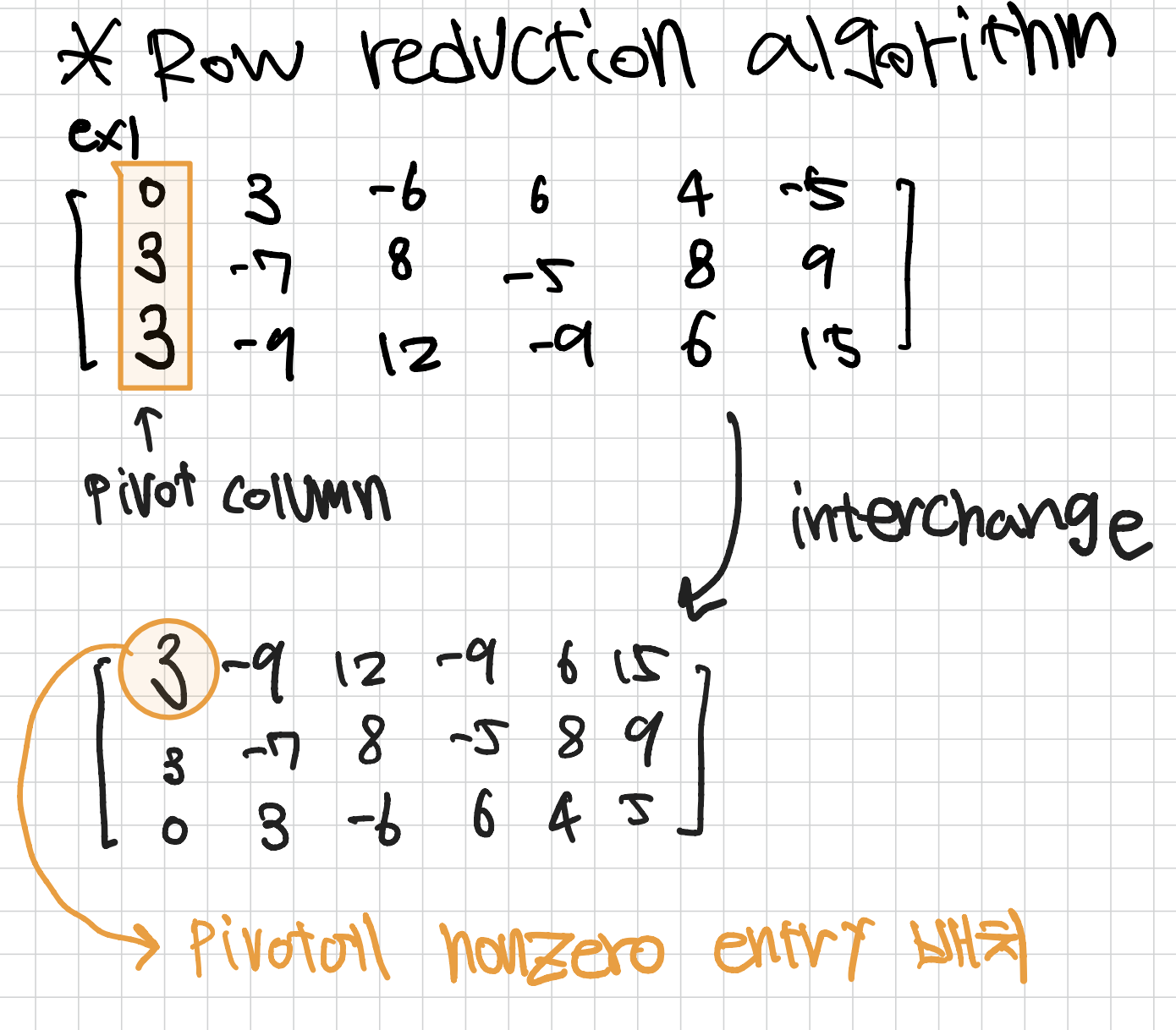
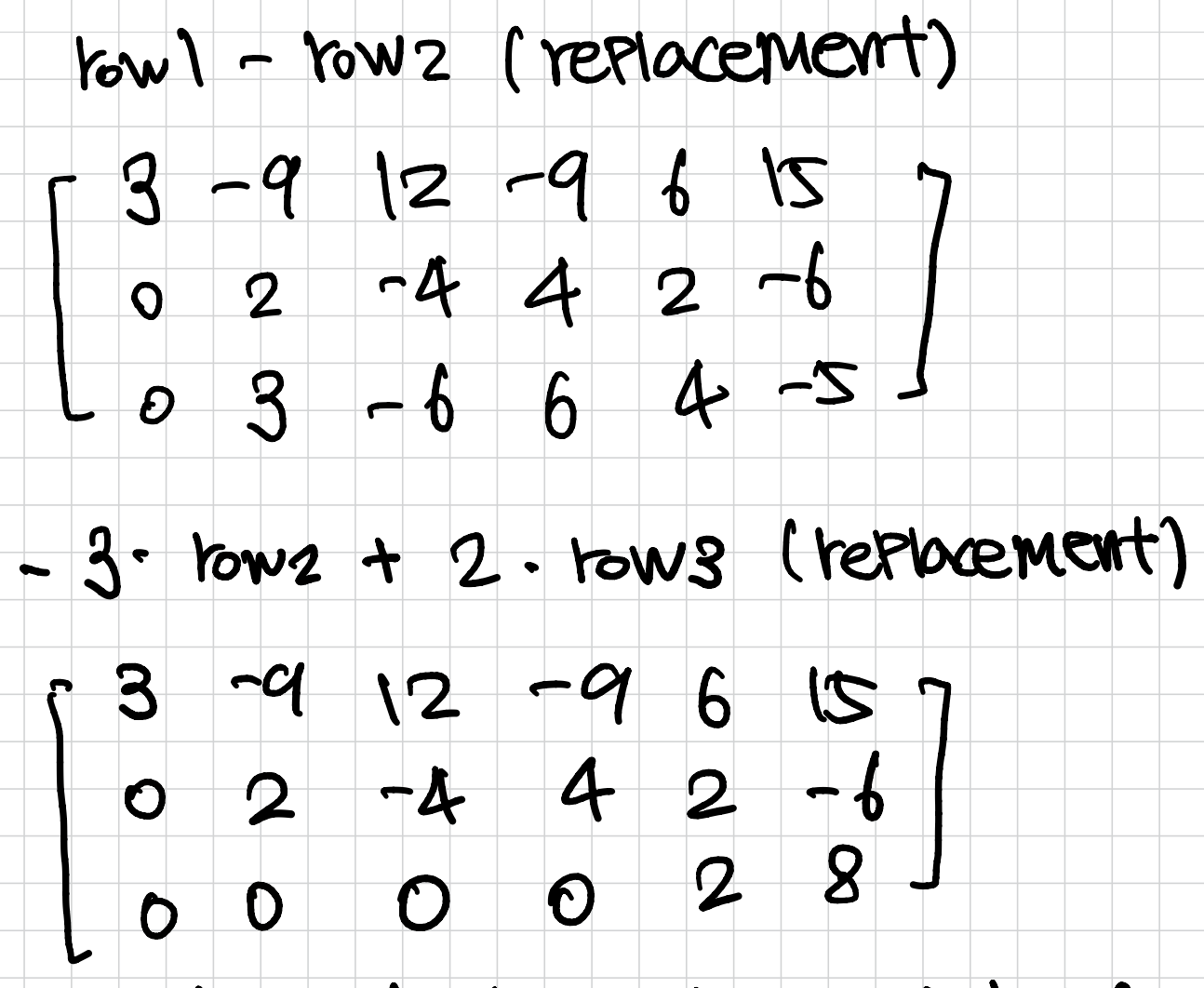
✔︎ forward phase (row echelon form을 만드는 과정)
✔︎ 가우스 소거법

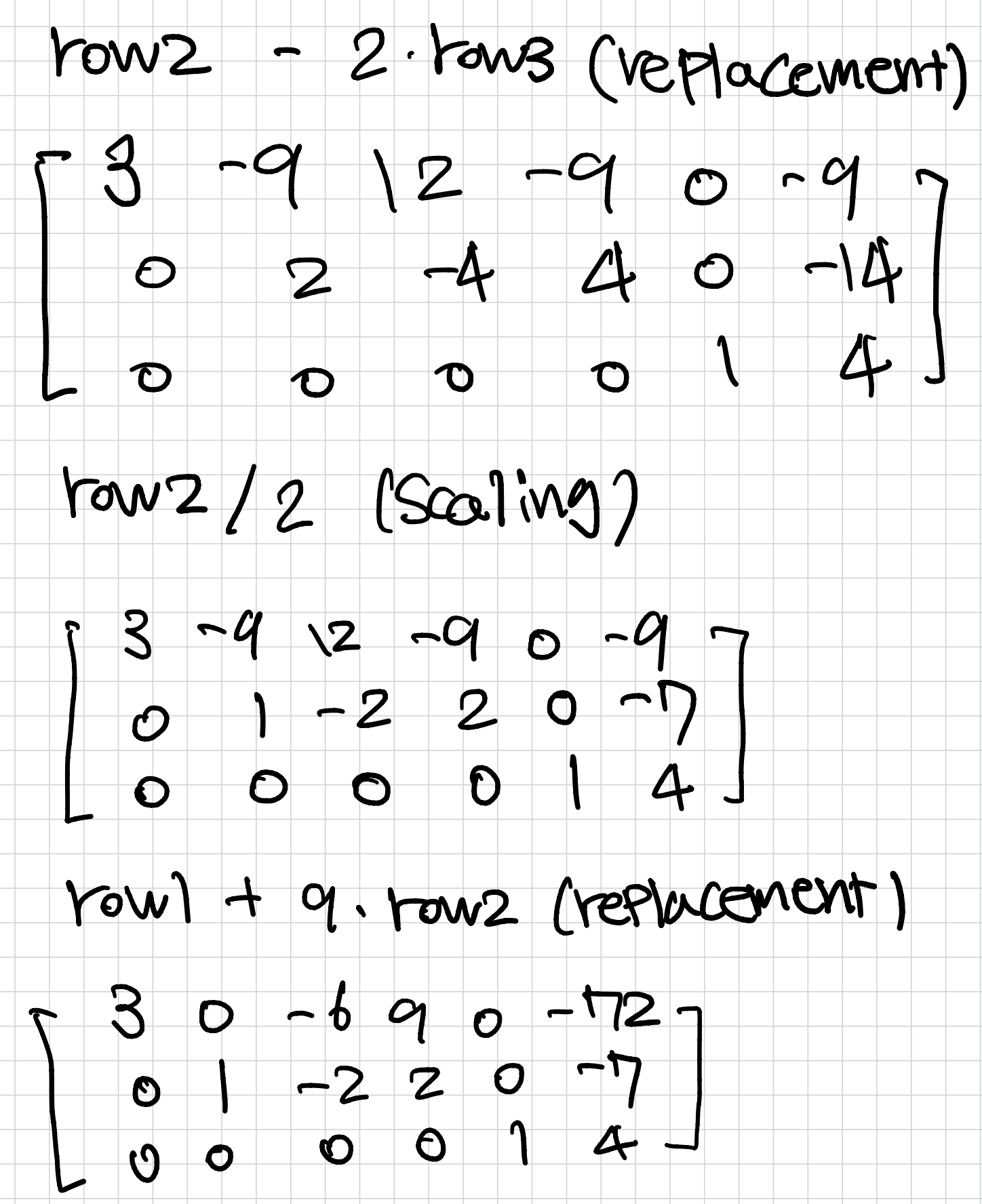
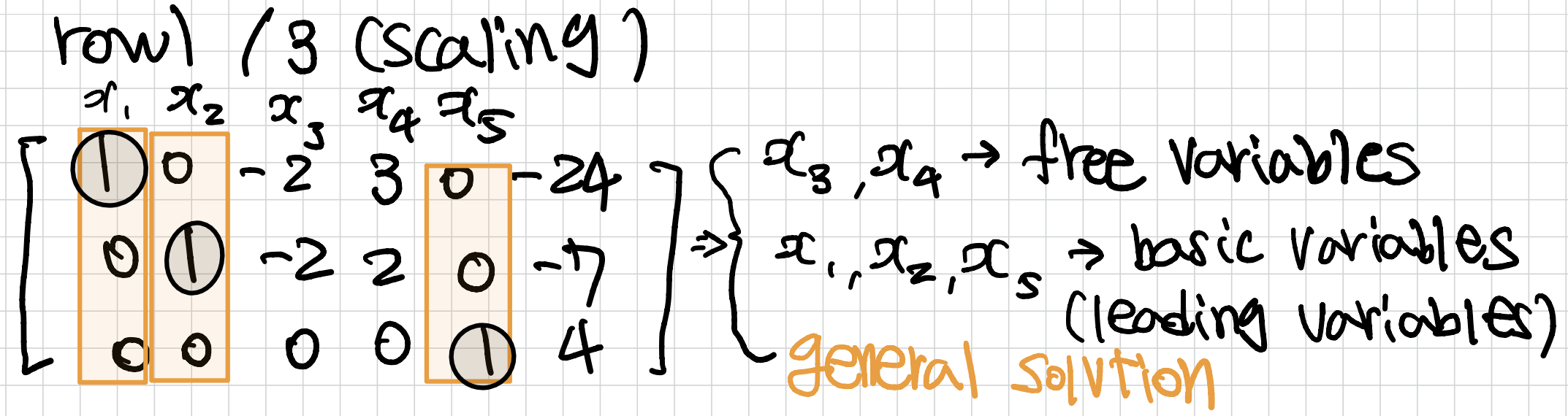
✔︎ backward phase (reduced row echelon form을 만드는 과정)
✔︎ 가우스-조단 소거법

Theorem. Existence and Uniqueness Theorem

• linear system이 inconsistent(해가 없는)한 것은 augmented matrix의 echelon form이 다음 그림과 같은 형태를 갖는 것과 동치이다.
  
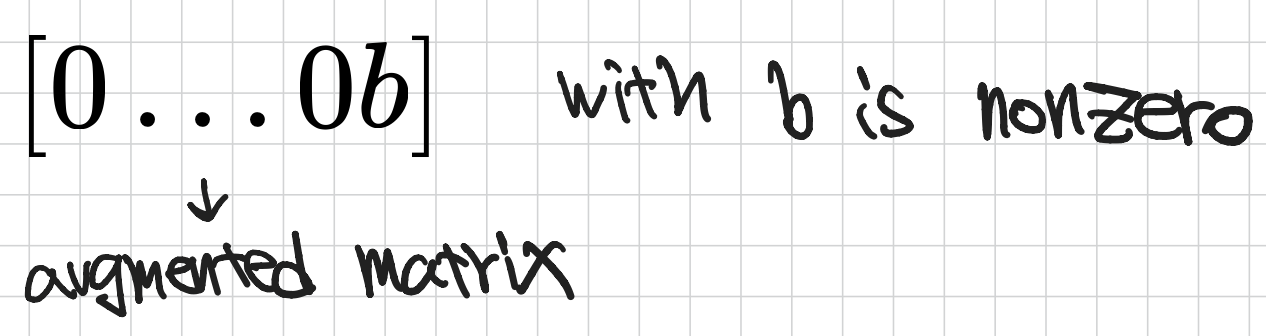
• linear system이 consistent(해를 갖는)면, free variable이 없을 때 unique한 solution을 갖고 적어도 하나의 free variable이 있을 때 infinitely(무수히) 많은 solution을 갖는다.

출처 및 참조

1. 한 걸음씩 알아가는 선형대수학, Kuldeep Singh, 한빛아카데미
2. 선형대수학개론, 인프런, 조범희 강좌